GMM检查方法#

高斯混合模型中不同初始化方法的示例

看到高斯混合模型有关估计器的更多信息。

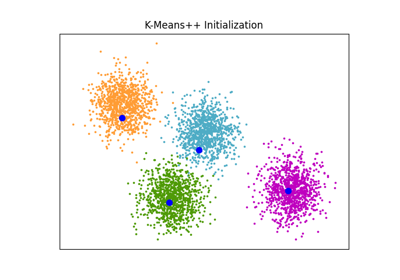
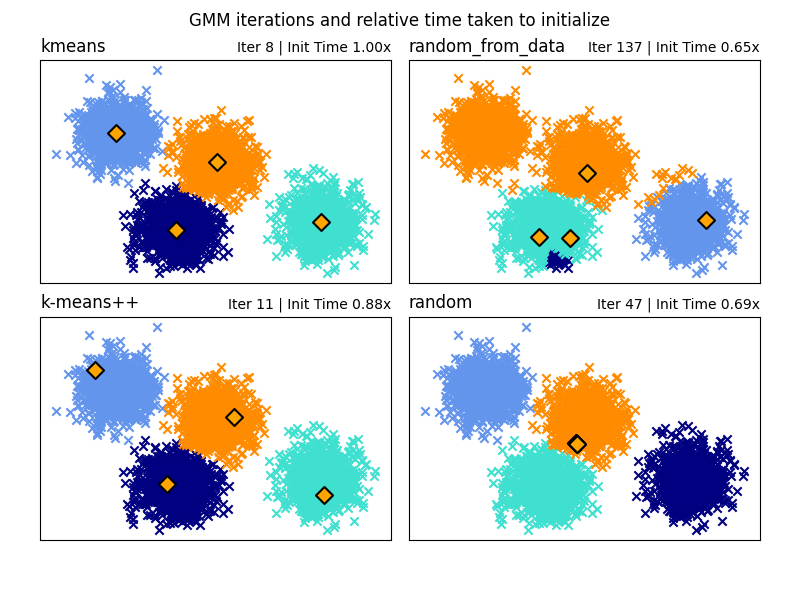
在这里，我们生成一些具有四个易于识别的集群的样本数据。此示例的目的是展示初始化参数的四种不同方法 init_param .

四个初始化是 kmeans （默认）， random , random_from_data 和 k-means++ .

橙色钻石代表由 init_param .其余的数据表示为十字，颜色表示GMM完成后的最终相关分类。

每个子图右上角的数字表示GaussianMixture收敛所需的迭代次数以及算法初始化部分运行所需的相对时间。较短的初始化时间往往有更多的迭代收敛。

初始化时间是该方法所花费的时间与默认方法所花费的时间的比率 kmeans 法正如您所看到的，与 kmeans .

在本例中，当初始化为 random_from_data 或 random 该模型需要更多迭代才能收敛。这里 k-means++ 在初始化时间短和收敛GaussianMixture迭代次数少方面都做得很好。

GMM iterations and relative time taken to initialize, kmeans, Iter 8 | Init Time 1.00x, random_from_data, Iter 137 | Init Time 0.65x, k-means++, Iter 11 | Init Time 0.88x, random, Iter 47 | Init Time 0.69x

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from timeit import default_timer as timer

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets._samples_generator import make_blobs
from sklearn.mixture import GaussianMixture
from sklearn.utils.extmath import row_norms

print(__doc__)

# Generate some data

X, y_true = make_blobs(n_samples=4000, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1]

n_samples = 4000
n_components = 4
x_squared_norms = row_norms(X, squared=True)


def get_initial_means(X, init_params, r):
    # Run a GaussianMixture with max_iter=0 to output the initialization means
    gmm = GaussianMixture(
        n_components=4, init_params=init_params, tol=1e-9, max_iter=0, random_state=r
    ).fit(X)
    return gmm.means_


methods = ["kmeans", "random_from_data", "k-means++", "random"]
colors = ["navy", "turquoise", "cornflowerblue", "darkorange"]
times_init = {}
relative_times = {}

plt.figure(figsize=(4 * len(methods) // 2, 6))
plt.subplots_adjust(
    bottom=0.1, top=0.9, hspace=0.15, wspace=0.05, left=0.05, right=0.95
)

for n, method in enumerate(methods):
    r = np.random.RandomState(seed=1234)
    plt.subplot(2, len(methods) // 2, n + 1)

    start = timer()
    ini = get_initial_means(X, method, r)
    end = timer()
    init_time = end - start

    gmm = GaussianMixture(
        n_components=4, means_init=ini, tol=1e-9, max_iter=2000, random_state=r
    ).fit(X)

    times_init[method] = init_time
    for i, color in enumerate(colors):
        data = X[gmm.predict(X) == i]
        plt.scatter(data[:, 0], data[:, 1], color=color, marker="x")

    plt.scatter(
        ini[:, 0], ini[:, 1], s=75, marker="D", c="orange", lw=1.5, edgecolors="black"
    )
    relative_times[method] = times_init[method] / times_init[methods[0]]

    plt.xticks(())
    plt.yticks(())
    plt.title(method, loc="left", fontsize=12)
    plt.title(
        "Iter %i | Init Time %.2fx" % (gmm.n_iter_, relative_times[method]),
        loc="right",
        fontsize=10,
    )
plt.suptitle("GMM iterations and relative time taken to initialize")
plt.show()

Total running time of the script: （0分0.815秒）