2.1. 高斯混合模型

sklearn.mixture 是一个软件包，使人们能够学习高斯混合模型（支持对角，球形，捆绑和全协方差矩阵），对其进行采样，并从数据中估计它们。还提供了帮助确定组件的适当数量的设施。

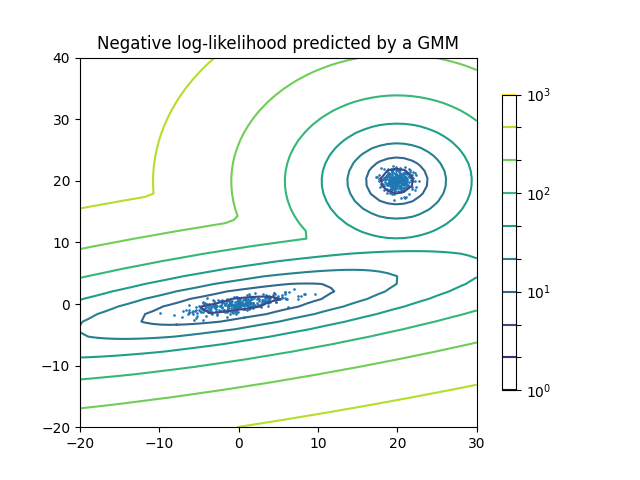
Two-component Gaussian mixture model: data points, and equi-probability surfaces of the model.

高斯混合模型是一种概率模型，假设所有数据点都是从有限数量的具有未知参数的高斯分布的混合中生成的。人们可以将混合模型视为推广k均值集群，以纳入有关数据协方差结构以及潜在高斯中心的信息。

Scikit-learn实现不同的类来估计高斯混合模型，这些模型对应于不同的估计策略，详细说明如下。

2.1.1. 高斯混合

的 GaussianMixture 对象实现 expectation-maximization (EM)适合高斯混合模型的算法。它还可以为多元模型绘制置信椭圆体，并计算Bayesian信息准则以评估数据中的集群数量。一 GaussianMixture.fit 提供了从训练数据学习高斯混合模型的方法。给定测试数据，它可以使用 GaussianMixture.predict 法

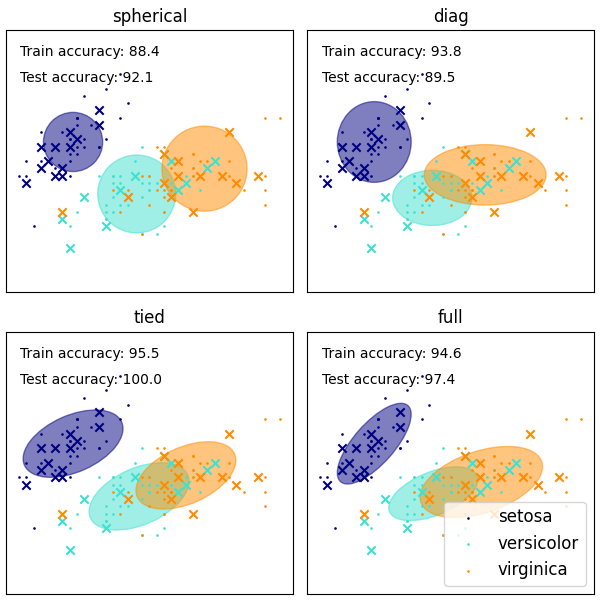
的 GaussianMixture 具有不同的选项来约束估计差异类别的协方差：球形、对角线、束缚或完全协方差。

示例

• 看到 GMM协方差 例如，使用高斯混合作为虹膜数据集的集群。

• 看到 高斯混合物的密度估计 例如绘制密度估计。

高斯混合物类的优点和缺点

优点

速度:

It is the fastest algorithm for learning mixture models

不可知:

由于该算法仅最大化了可能性，因此它不会将均值偏向零，也不会将集群大小偏向于具有可能适用或可能不适用的特定结构。

缺点

奇点:

当每个混合物的点不够多时，估计协方差矩阵就会变得困难，并且已知算法会以无限可能性进行分歧并找到解，除非人为地调整协方差。

数量的部件:

该算法将始终使用它可以访问的所有组件，需要提供的数据或信息理论标准来决定在没有外部线索的情况下使用多少组件。

选择经典高斯混合模型中的分量数

CIC准则可用于以有效的方式选择高斯混合中的分量数量。从理论上讲，它仅在渐进机制中恢复分量的真实数量（即，如果有大量数据可用，并假设数据实际上是i. i. d生成的。来自高斯分布的混合）。请注意，使用 Variational Bayesian Gaussian mixture 避免指定高斯混合模型的分量数量。

示例

• 看到 高斯混合模型选择 对于使用经典高斯混合执行的模型选择的示例。

估计算法期望最大化

从未标记数据学习高斯混合模型的主要困难是，人们通常不知道哪些点来自哪个潜在分量（如果可以访问此信息，那么就很容易将单独的高斯分布与每套点匹配）。 Expectation-maximization 是一种有充分依据的统计算法，可以通过迭代过程解决这个问题。第一个假设随机分量（随机以数据点为中心，从k均值学习，甚至只是正态分布在原点周围），并为每个点计算模型的每个分量生成的概率。然后，调整参数，以最大化给定这些分配的数据的可能性。重复此过程可以保证始终收敛到局部最优值。

收件箱方法的选择

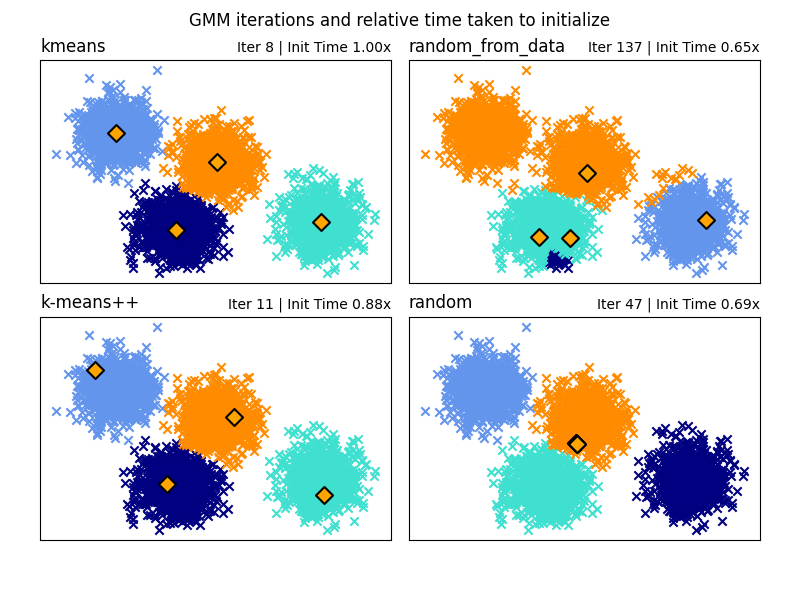
可以选择四种初始化方法（以及输入用户定义的初始平均值）来生成模型组件的初始中心：

k均值（默认）

这应用了传统的k均值集群算法。与其他初始化方法相比，这在计算上可能会很昂贵。

k均值++

这使用k-means集群的初始化方法：k-means++。这将从数据中随机选择第一个中心。后续中心将从数据的加权分布中选择，这些数据有利于距离现有中心更远的点。k-means++是k-means的默认初始化，因此将比运行完整的k-means更快，但对于具有许多组件的大型数据集来说仍然需要大量时间。

random_from_data

这将从输入数据中挑选随机数据点作为初始中心。这是一种非常快速的初始化方法，但如果选择的点彼此太近，可能会产生非收敛的结果。

随机

选择中心作为远离所有数据平均值的小扰动。这种方法很简单，但可能导致模型需要更长的时间才能收敛。

示例

• 看到 GMM检查方法 例如，在高斯混合中使用不同初始化。

2.1.2. 变分Bayesian高斯混合

的 BayesianGaussianMixture 对象使用变分推理算法实现高斯混合模型的变体。该API类似于 GaussianMixture .

Estimation algorithm: variational inference

变分推理是期望最大化的扩展，它最大化模型证据（包括先验）而不是数据可能性的下限。变分方法背后的原理与期望最大化相同（即两者都是迭代算法，在寻找每个混合物生成的每个点的概率和将混合物匹配到这些指定点之间交替），但变分方法通过集成来自先验分布的信息来添加规则化。这避免了期望最大化解决方案中常见的奇异性，但给模型带来了一些微妙的偏差。推理通常速度明显较慢，但通常不会慢到以至于使用不切实际。

由于其Bayesian性质，变分算法需要比期望最大化更多的超参数，其中最重要的是浓度参数 weight_concentration_prior .将浓度指定为较低的值将使模型将大部分重量放在少数成分上，并将其余成分的重量设置为非常接近零。浓度先验的高值将允许更大数量的组分在混合物中具有活性。

的参数实现 BayesianGaussianMixture 类为权重分布提出了两种类型的先验：具有Dirichlet分布的有限混合模型和具有Dirichlet过程的无限混合模型。在实践中，Dirichlet Process推理算法是近似的，并使用具有固定最大分量数量的截断分布（称为Stick-breaking表示）。实际使用的组件数量几乎总是取决于数据。

下图比较了不同类型的重量浓度之前获得的结果（参数 weight_concentration_prior_type ）对于不同的 weight_concentration_prior .在这里，我们可以看到 weight_concentration_prior 参数对获得的活性成分的有效数量有很大影响。我们还可以注意到，当先验类型为“dirichlet_disposal”时，浓度权重先验的大值会导致权重更均匀，而对于“dirichlet_Process”类型（默认使用）来说，情况不一定是这样。

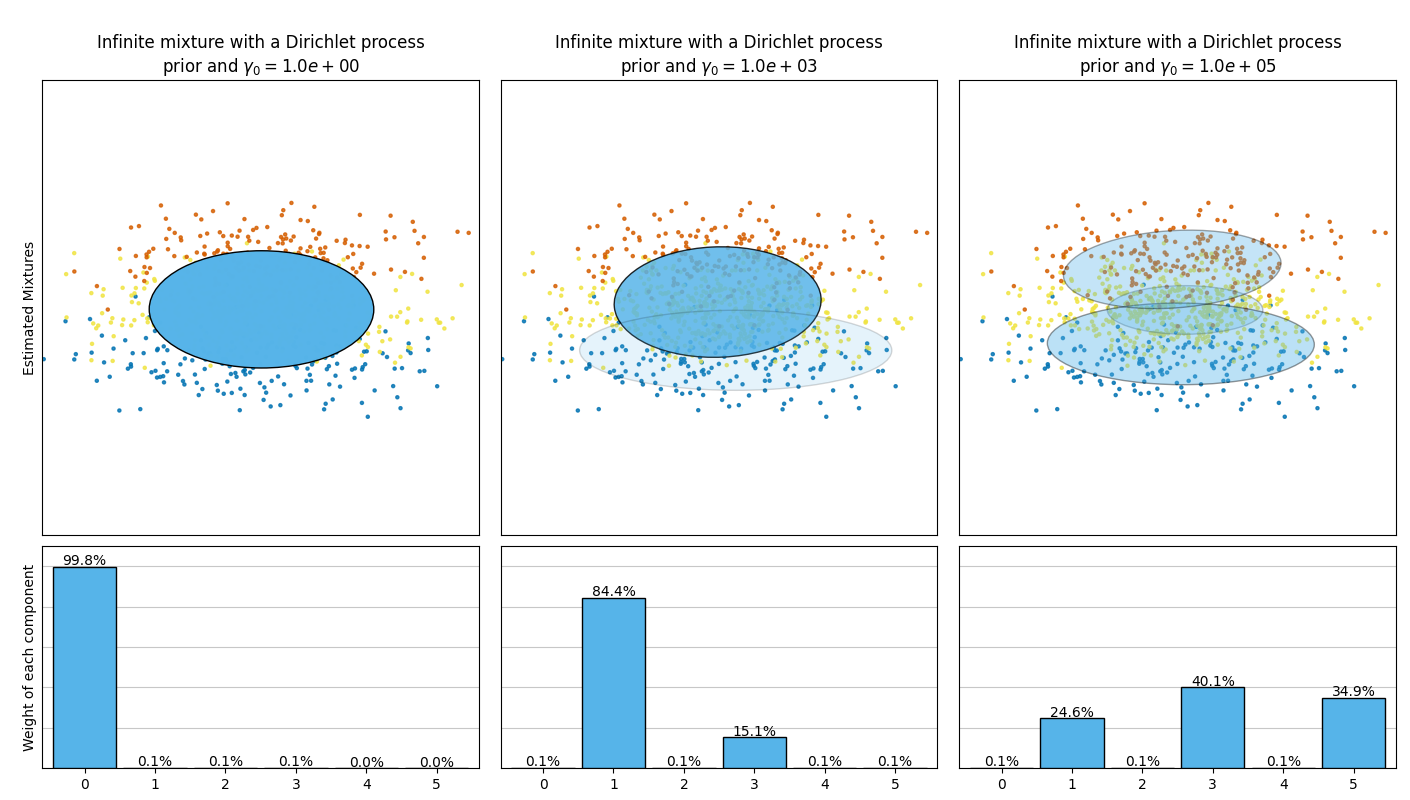
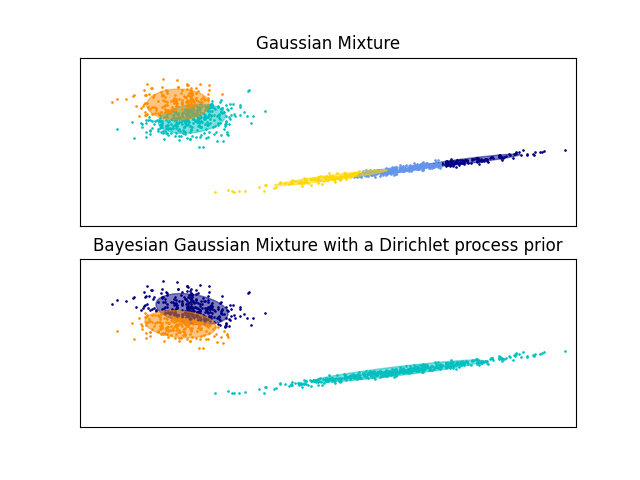
下面的示例将具有固定数量分量的高斯混合模型与具有Dirichlet过程的变分高斯混合模型进行比较。在这里，经典高斯混合在由2个集群组成的数据集上用5个分量进行匹配。我们可以看到，具有Dirichlet过程先验的变分高斯混合能够将自己限制为仅2个分量，而高斯混合用固定数量的分量来匹配数据，这些分量必须由用户先验设置。在这种情况下，用户已选择 n_components=5 这与这个玩具数据集的真实生成分布不匹配。请注意，在观察很少的情况下，具有Dirichlet过程的变分高斯混合模型可以采取保守立场，并且仅适合一个分量。

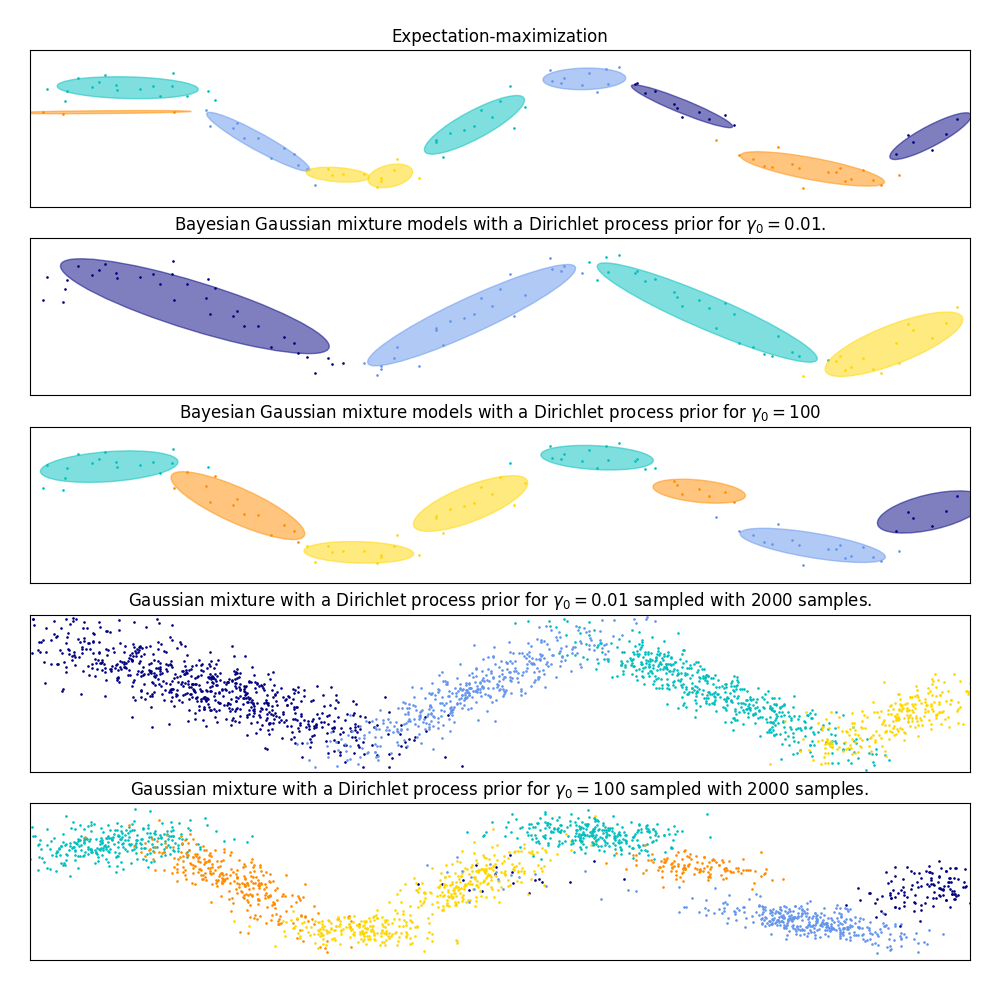
在下图中，我们正在对高斯混合没有很好地描述的数据集进行匹配。调整 weight_concentration_prior ，的参数 BayesianGaussianMixture 控制用于适应此数据的组件数量。我们还在最后两个图上呈现了从两种所得混合物生成的随机抽样。

示例

• 看到 高斯混合模型椭圆体 例如，绘制两者的置信椭圆体 GaussianMixture 和 BayesianGaussianMixture .

• 高斯混合模型顺曲线 显示使用 GaussianMixture 和 BayesianGaussianMixture 以适应一个长波。

• See 变异Bayesian高斯混合物的浓度先验型分析 for an example plotting the confidence ellipsoids for the BayesianGaussianMixture with different weight_concentration_prior_type for different values of the parameter weight_concentration_prior.

Bayesian GaussianMixture变分推理的利弊

优点

自动选择:

当 weight_concentration_prior 足够小， n_components 大于模型发现的必要值，变分Bayesian混合模型自然倾向于将一些混合权重值设置为接近零。这使得模型可以自动选择合适数量的有效组件。仅需要提供该数字的上限。但请注意，活动组件的“理想”数量非常特定于应用程序，并且在数据探索环境中通常定义不清。

对参数数量的敏感性较低:

与有限模型不同，有限模型几乎总是尽可能多地使用所有组件，因此将为不同数量的组件产生截然不同的解决方案，具有Dirichlet过程的变分推理 (weight_concentration_prior_type='dirichlet_process' ）不会随着参数的变化而发生太大变化，从而导致更高的稳定性和更少的调整。

正则化:

由于引入了先验信息，变分解比期望最大化解具有更少的病态特例。

缺点

速度:

变分推理所需的额外参数化使推理速度变慢，尽管速度不会太慢。

超参数:

该算法需要一个额外的超参数，可能需要通过交叉验证进行实验性调整。

偏置:

在推理算法中有许多隐含的偏差（如果使用狄利克雷过程，也是如此），只要这些偏差和数据之间存在不匹配，就有可能使用有限混合来拟合更好的模型。

2.1.2.1. 狄利克雷过程

在这里，我们描述了Dirichlet过程混合的变分推理算法。Dirichlet过程是一个先验概率分布 clusterings with an infinite, unbounded, number of partitions .与有限高斯混合模型相比，变分技术让我们在推理时间上几乎没有损失的情况下将这种先验结构整合到高斯混合模型上。

一个重要的问题是Dirichlet过程如何使用无限、无限数量的集群并且仍然保持一致。虽然完整的解释不适合本手册，但人们可以想到它的 stick breaking process 类比以帮助理解它。打破大棒的过程是狄利克雷过程的一个生成故事。我们从一根单位长度的棍子开始，在每一步中，我们都会折断剩余棍子的一部分。每次，我们都会将木棍的长度与落入混合物组中的点的比例联系起来。最后，为了表示无限混合物，我们将棍子的最后一部分与不属于所有其他组的点的比例联系起来。每块的长度是一个随机变量，其概率与浓度参数成正比。浓度的较小值将将单位长度分成更大的棒块（定义更集中的分布）。更大的浓度值将产生更小的棒块（增加具有非零重量的成分的数量）。

Dirichlet过程的变分推理技术仍然适用于这个无限混合物模型的有限逼近，但不必先验地指定想要使用多少成分，而只需指定浓度参数和混合物成分数量的上限（假设这个上限高于组件的“真实”数量，则只影响算法复杂性，而不影响所使用组件的实际数量）。