Ctrl+K

1.5. 随机梯度下降#

Stochastic Gradient Descent (SGD) 是一种简单但非常有效的方法，可以在凸损失函数（线性）下匹配线性分类器和回归器 Support Vector Machines 和 Logistic Regression .尽管BCD在机器学习领域已经存在很长时间，但最近在大规模学习的背景下，它才受到了相当多的关注。

BCD已成功应用于文本分类和自然语言处理中经常遇到的大规模和稀疏机器学习问题。 鉴于数据是稀疏的，此模块中的分类器可以轻松扩展到具有超过 \(10^5\) 训练样本和超过 \(10^5\) 功能.

严格来说，BCD只是一种优化技术，并不对应于特定的机器学习模型家族。它只是一个 way 训练一个模型。通常情况下， SGDClassifier 或 SGDRegressor scikit-learn API中将有一个等效的估计器，可能使用不同的优化技术。例如使用 SGDClassifier(loss='log_loss') 导致逻辑回归，即相当于 LogisticRegression 它是通过新元进行安装的，而不是由其他解算者之一进行安装的 LogisticRegression .同样， SGDRegressor(loss='squared_error', penalty='l2') 和 Ridge 通过不同的方式解决相同的优化问题。

随机梯度下降的优点是：

  • 效率

  • 易于实现（有很多代码调优的机会）。

随机梯度下降的缺点包括：

  • BCD需要许多超参数，例如正规化参数和迭代次数。

  • SGD对功能缩放敏感。

警告

确保在适应模型或使用之前排列（洗牌）您的训练数据 shuffle=True 在每次迭代后进行洗牌（默认使用）。此外，理想情况下，应使用例如 make_pipeline(StandardScaler(), SGDClassifier()) （见 Pipelines ).

1.5.1. 分类#

类 SGDClassifier 实现了一个简单的随机梯度下降学习例程，该例程支持不同的损失函数和分类惩罚。以下是a的决策边界 SGDClassifier 用铰链损失进行训练，相当于线性支持机。

../_images/sphx_glr_plot_sgd_separating_hyperplane_001.png

与其他分类器一样，BCD必须配备两个阵列：一个阵列 X 包含训练样本的形状（n_samples，n_features）和数组 y 保存训练样本目标值（类标签）的形状（n_samples，）：

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

匹配后，模型可用于预测新值：：

>>> clf.predict([[2., 2.]])
array([1])

BCD将线性模型与训练数据进行匹配。的 coef_ 属性保存模型参数：：

>>> clf.coef_
array([[9.9, 9.9]])

的 intercept_ 属性保存截距（也称为偏移或偏差）：：

>>> clf.intercept_
array([-9.9])

模型是否应该使用拦截（即有偏超平面）由参数控制 fit_intercept .

到超平面的带符号距离（计算为系数和输入样本之间的点积加上相交）由下式给出 SGDClassifier.decision_function

>>> clf.decision_function([[2., 2.]])
array([29.6])

具体损失功能可通过设置 loss 参数. SGDClassifier 支持以下丢失功能：

  • loss="hinge" ：（软利润）线性支持向量机，

  • loss="modified_huber" ：平滑铰链损失，

  • loss="log_loss" ：逻辑回归，

  • 以及下面的所有回归损失。在这种情况下，目标编码为 \(-1\) 或 \(1\) ，并且该问题被视为回归问题。然后，预测的类别对应于预测目标的符号。

请参阅 mathematical section below 对于公式。前两个损失函数是懒惰的，它们仅在示例违反裕度约束的情况下更新模型参数，这使得训练非常高效，并且可能会导致更稀疏的模型（即具有更多零系数），即使当 \(L_2\) 使用惩罚。

使用 loss="log_loss" 或 loss="modified_huber" 使得 predict_proba 方法，它给出了概率估计的一个载体 \(P(y|x)\) 每个样品 \(x\)

>>> clf = SGDClassifier(loss="log_loss", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]])
array([[0.00, 0.99]])

具体处罚可以通过 penalty 参数.新元支持以下处罚：

  • penalty="l2": \(L_2\) 规范处罚 coef_ .

  • penalty="l1": \(L_1\) 规范处罚 coef_ .

  • penalty="elasticnet" ：凸组合 \(L_2\) 和 \(L_1\) ; (1 - l1_ratio) * L2 + l1_ratio * L1 .

默认设置为 penalty="l2" .的 \(L_1\) 惩罚导致稀疏解，使大多数系数变为零。弹性网络 [11] 解决了 \(L_1\) 存在高度相关的属性时的处罚。参数 l1_ratio 控制的凸组合 \(L_1\) 和 \(L_2\) 点球

SGDClassifier 通过将多个二进制分类器组合在“一对所有”（UVA）方案中，支持多类分类。中的每 \(K\) 类中，学习一个二元分类器，可以区分该分类器和所有其他分类器 \(K-1\) 班在测试时，我们计算每个分类器的置信度分数（即到超平面的带符号距离），并选择置信度最高的类别。下图说明了虹膜数据集上的UVA方法。 虚线代表三个UVA分类器;背景颜色显示由三个分类器引发的决策表面。

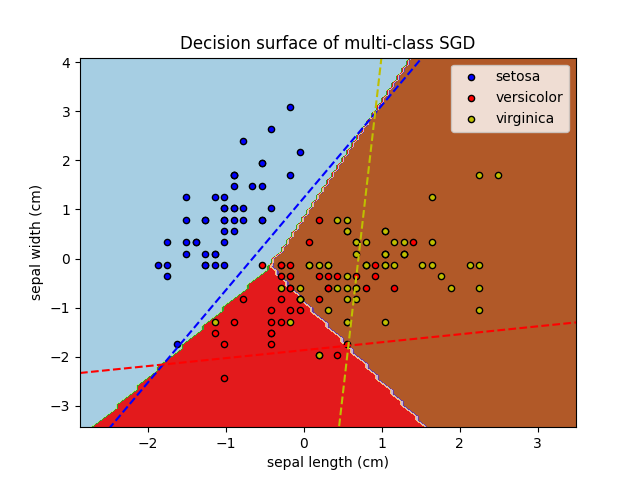
../_images/sphx_glr_plot_sgd_iris_001.png

在多类别分类的情况下 coef_ 是形状的二维数组（n_classes，n_features）和 intercept_ 是形状的一维数组（n_classes，）。的 \(i\) 第-行 coef_ 保存的UVA分类器的权重载体 \(i\) -th类;类按递进顺序编制索引（请参阅属性 classes_ ).请注意，原则上，由于它们允许创建概率模型， loss="log_loss" 和 loss="modified_huber" 更适合一体化分类。

SGDClassifier 通过匹配参数支持加权类和加权实例 class_weight 和 sample_weight .请参阅下面的示例和 SGDClassifier.fit 获取更多信息.

SGDClassifier supports averaged SGD (ASGD) [10]. Averaging can be enabled by setting average=True. ASGD performs the same updates as the regular SGD (see 数学公式), but instead of using the last value of the coefficients as the coef_ attribute (i.e. the values of the last update), coef_ is set instead to the average value of the coefficients across all updates. The same is done for the intercept_ attribute. When using ASGD the learning rate can be larger and even constant, leading on some datasets to a speed up in training time.

对于具有后勤损失的分类，具有平均策略的另一种SGD变体可通过随机平均梯度（SAG）算法获得，该算法可用作中的求解器 LogisticRegression .

示例

1.5.2. 回归#

类 SGDRegressor 实现了一个简单的随机梯度下降学习例程，该例程支持不同的损失函数和惩罚来适应线性回归模型。 SGDRegressor 非常适合具有大量训练样本（> 10.000）的回归问题，对于我们推荐的其他问题 Ridge , Lasso ，或者 ElasticNet .

具体损失功能可通过设置 loss 参数. SGDRegressor 支持以下丢失功能：

  • loss="squared_error" ：普通最小平方，

  • loss="huber" ：胡贝尔因稳健回归而损失，

  • loss="epsilon_insensitive" ：线性支持载体回归。

请参阅 mathematical section below 对于公式。Huber和Epsilon不敏感损失函数可用于鲁棒回归。不敏感区域的宽度必须通过参数指定 epsilon .此参数取决于目标变量的规模。

的 penalty 参数确定要使用的正规化（请参阅上面分类部分的描述）。

SGDRegressor 还支持平均新元 [10] (here再次请参阅上面分类部分的描述）。

对于具有平方损失和 \(L_2\) 惩罚，另一种具有平均策略的SGD变体可通过随机平均梯度（SAG）算法获得，可作为中的求解器提供 Ridge .

1.5.3. 在线一类支持者#

类 sklearn.linear_model.SGDOneClassSVM 使用随机梯度下降实现单类支持机的在线线性版本。结合核逼近技术， sklearn.linear_model.SGDOneClassSVM 可用于逼近核化单类支持机的解，在 sklearn.svm.OneClassSVM ，样本数量呈线性复杂性。请注意，核化的一类支持者的复杂性充其量是样本数量的二次。 sklearn.linear_model.SGDOneClassSVM 因此，非常适合具有大量训练样本（超过10，000个）的数据集，对于这些样本，BCD变体可以快几个数量级。

数学细节#

它的实现基于随机梯度下降的实现。事实上，一类支持者的原始优化问题由下式给出

\[\begin{split}\begin{aligned} \min_{w, \rho, \xi} & \quad \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \xi_i \\ \text{s.t.} & \quad \langle w, x_i \rangle \geq \rho - \xi_i \quad 1 \leq i \leq n \\ & \quad \xi_i \geq 0 \quad 1 \leq i \leq n \end{aligned}\end{split}\]

哪里 \(\nu \in (0, 1]\) 是用户指定的参数，用于控制异常值比例和支持量比例。摆脱松弛变量 \(\xi_i\) 这个问题相当于

\[\min_{w, \rho} \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \max(0, \rho - \langle w, x_i \rangle) \, .\]

乘以常数 \(\nu\) 并引入拦截 \(b = 1 - \rho\) 我们得到以下等效优化问题

\[\min_{w, b} \frac{\nu}{2}\Vert w \Vert^2 + b\nu + \frac{1}{n} \sum_{i=1}^n \max(0, 1 - (\langle w, x_i \rangle + b)) \, .\]

This is similar to the optimization problems studied in section 数学公式 with \(y_i = 1, 1 \leq i \leq n\) and \(\alpha = \nu/2\), \(L\) being the hinge loss function and \(R\) being the \(L_2\) norm. We just need to add the term \(b\nu\) in the optimization loop.

作为 SGDClassifier 和 SGDRegressor , SGDOneClassSVM 支持平均新元。可以通过设置启用平均 average=True .

示例

1.5.4. 稀疏数据的随机梯度下降#

备注

稀疏实现产生的结果与密集实现略有不同，这是由于截距的学习率缩小了。看到 实现细节 .

对任何矩阵中给出的稀疏数据都内置支持，其格式为 scipy.sparse .但是，为了最大限度地提高效率，请使用中定义的CSR矩阵格式 scipy.sparse.csr_matrix .

示例

1.5.5. 复杂性#

BCD的主要优势是其效率，其效率与训练示例数量基本呈线性关系。如果 \(X\) 是一个大小矩阵 \(n \times p\) （与 \(n\) 样品和 \(p\) 功能），培训的成本 \(O(k n \bar p)\) ，在哪里 \(k\) 是迭代（历元）的数量， \(\bar p\) 是每个样本非零属性的平均数。

Recent theoretical results, however, show that the runtime to get some desired optimization accuracy does not increase as the training set size increases.

1.5.6. 停止标准#

的类 SGDClassifier 和 SGDRegressor 当达到给定收敛水平时，提供两个标准来停止算法：

  • 与 early_stopping=True ，输入数据被分成训练集和验证集。然后将模型与训练集相匹配，停止标准基于预测分数（使用 score 方法）在验证集上计算。验证集的大小可以使用参数更改 validation_fraction .

  • 与 early_stopping=False 时，模型在整个输入数据上进行匹配，停止标准基于在训练数据上计算的目标函数。

在这两种情况下，标准都会按历元评估一次，当标准没有改善时，算法就会停止 n_iter_no_change 连续几次。用绝对公差评价改善情况 tol ，并且算法在任何情况下都会在最大迭代次数后停止 max_iter .

看到 随机梯度下降的早停止 作为提前停止影响的一个例子。

1.5.7. 实际使用技巧#

  • 随机梯度下降对特征缩放很敏感，因此强烈建议扩展您的数据。例如，缩放输入载体上的每个属性 \(X\) 到 \([0,1]\) 或 \([-1,1]\) ，或者标准化它具有平均值 \(0\) 和方差 \(1\) .注意到 same 必须将缩放应用于测试载体才能获得有意义的结果。这可以通过使用轻松完成 StandardScaler

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

# Or better yet: use a pipeline!
from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

    如果您的属性具有内在规模（例如词频或指标特征），则不需要进行缩放。

  • 寻找合理的正规化术语 \(\alpha\) 最好使用自动超参数搜索来完成，例如 GridSearchCV 或 RandomizedSearchCV ，通常在范围内 10.0**-np.arange(1,7) .

  • 从经验上看，我们发现新元经过大约观察后收敛 \(10^6\) 训练样本。因此，对迭代次数的合理初步猜测是 max_iter = np.ceil(10**6 / n) ，在哪里 n 是训练集的大小。

  • 如果您将BCD应用于使用PCA提取的特征，我们发现将特征值按某个常数缩放通常是明智的 c 使得平均 \(L_2\) 训练数据的规范等于1。

  • 我们发现，平均新元在功能数量较多且功能更高的情况下效果最佳 eta0 .

引用

  • "Efficient BackProp" Y.莱昆湖博图，G.奥尔，K.穆勒-《神经网络：贸易技巧》1998年。

1.5.8. 数学公式#

我们在这里描述了BCD过程的数学细节。关于收敛率的良好概述请参阅 [12].

Given a set of training examples \((x_1, y_1), \ldots, (x_n, y_n)\) where \(x_i \in \mathbf{R}^m\) and \(y_i \in \mathbf{R}\) (\(y_i \in \{-1, 1\}\) for classification), our goal is to learn a linear scoring function \(f(x) = w^T x + b\) with model parameters \(w \in \mathbf{R}^m\) and intercept \(b \in \mathbf{R}\). In order to make predictions for binary classification, we simply look at the sign of \(f(x)\). To find the model parameters, we minimize the regularized training error given by

\[E（w，b）= \fRAC{1}{n}\sum_{i=1}^{n} L（y_i，f（x_i））+ \Alpha R（w）\]

哪里 \(L\) 是一个损失函数，用于衡量模型（错误）适合度， \(R\) 是惩罚模型复杂性的正规化项（又名罚分）; \(\alpha > 0\) 是控制规则化强度的非负超参数。

损失功能详细信息#

选择不同的方式 \(L\) 需要不同的分类器或回归器：

  • Hinge（软边缘）：相当于支持向量分类。 \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))\) .

  • 感知器： \(L(y_i, f(x_i)) = \max(0, - y_i f(x_i))\) .

  • 修改后的胡贝尔： \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2\) 如果 \(y_i f(x_i) > -1\) ，而且 \(L(y_i, f(x_i)) = -4 y_i f(x_i)\) 否则。

  • Log Loss: equivalent to Logistic Regression. \(L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))\).

  • 平方误差：线性回归（Ridge或Lasso取决于 \(R\) ). \(L(y_i, f(x_i)) = \frac{1}{2}(y_i - f(x_i))^2\) .

  • Huber: less sensitive to outliers than least-squares. It is equivalent to least squares when \(|y_i - f(x_i)| \leq \varepsilon\), and \(L(y_i, f(x_i)) = \varepsilon |y_i - f(x_i)| - \frac{1}{2} \varepsilon^2\) otherwise.

  • Epsilon-Insensitive：（软利润）相当于支持量回归。 \(L(y_i, f(x_i)) = \max(0, |y_i - f(x_i)| - \varepsilon)\) .

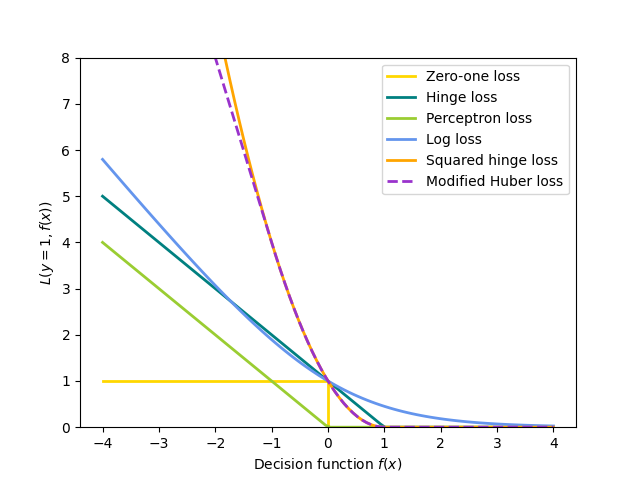
所有上述损失函数都可以被视为误分类误差（零一损失）的上限，如下图所示。

../_images/sphx_glr_plot_sgd_loss_functions_001.png

正规化术语的流行选择 \(R\) （The penalty 参数）包括：

  • \(L_2\) 规范： \(R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2\) ,

  • \(L_1\) 规范： \(R(w) := \sum_{j=1}^{m} |w_j|\) ，这会导致稀疏的解决方案。

  • Elastic Net: \(R(w) := \frac{\rho}{2} \sum_{j=1}^{n} w_j^2 + (1-\rho) \sum_{j=1}^{m} |w_j|\), a convex combination of \(L_2\) and \(L_1\), where \(\rho\) is given by 1 - l1_ratio.

下图显示了2维参数空间中不同正规化项的轮廓 (\(m=2\) ）当 \(R(w) = 1\) .

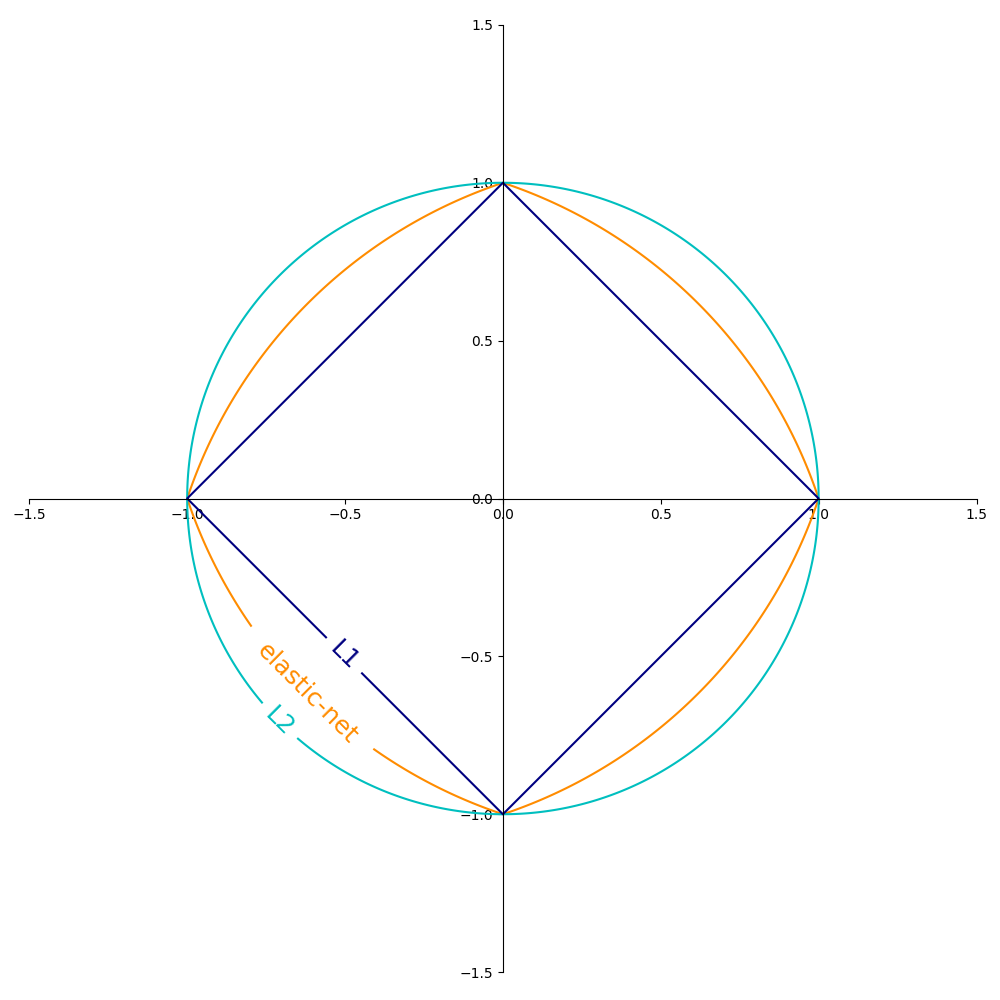
../_images/sphx_glr_plot_sgd_penalties_001.png

1.5.8.1. SGD#

随机梯度下降是一种针对无约束优化问题的优化方法。与（批量）梯度下降相反，BCD接近的真实梯度 \(E(w,b)\) 通过一次考虑单个训练示例。

类 SGDClassifier 实现一阶新元学习例程。 该算法迭代训练示例，并针对每个示例根据下式给出的更新规则更新模型参数

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]\]

哪里 \(\eta\) 是控制参数空间中步进大小的学习率。 截距 \(b\) 类似地更新，但没有正规化（并且对稀疏矩阵进行了额外的衰减，详细描述在 实现细节 ).

学习率 \(\eta\) 可以是持续的，也可以是逐渐衰变的。对于分类，默认学习率计划 (learning_rate='optimal' ）由

\[\eta^{（t）} = \fRAC {1}{\Alpha（t_0 + t）}\]

where \(t\) is the time step (there are a total of n_samples * n_iter time steps), \(t_0\) is determined based on a heuristic proposed by Léon Bottou such that the expected initial updates are comparable with the expected size of the weights (this assumes that the norm of the training samples is approximately 1). The exact definition can be found in _init_t in BaseSGD.

对于回归，默认学习率计划是逆缩放 (learning_rate='invscaling' ），给出者

\[\eta^{（t）} = \fRAC{eta_0}{t^{power\_t}\]

哪里 \(eta_0\) 和 \(power\_t\) 是用户通过以下方式选择的超参数： eta0 和 power_t ，分别。

对于恒定的学习率使用 learning_rate='constant' 和使用 eta0 以指定学习率。

为了自适应地降低学习率，请使用 learning_rate='adaptive' 和使用 eta0 指定开始学习率。当达到停止标准时，学习率除以5，算法不会停止。当学习率低于时，算法停止 1e-6 .

可以通过访问模型参数 coef_ 和 intercept_ 属性： coef_ 握住重量 \(w\) 和 intercept_ 持有 \(b\) .

当使用平均新元（与 average 参数）， coef_ 设置为所有更新的平均权重： coef_ \(= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}\) ，在哪里 \(T\) 是更新的总数，可在 t_ 属性

1.5.9. 实现细节#

新元的实施受到 Stochastic Gradient SVM 的 [7]. 与SvmBCD类似，权重载体被表示为纯量和载体的积，这允许在以下情况下进行有效的权重更新 \(L_2\) 正规化。在稀疏输入的情况下 X ，以较小的学习率（乘以0.01）更新拦截，以考虑其更新频率更高的事实。训练示例是顺序拾取的，并且在每个观察到的示例后学习率会降低。我们采用了来自 [8]. 对于多类别分类，使用“一对所有”的方法。我们使用中提出的截断梯度算法 [9] 为 \(L_1\) 正规化（和弹性网络）。代码是用Cython编写的。

引用

On this page