2.2. 流形学习#
总管学习是一种非线性降维的方法。这项任务的算法基于这样的想法:许多数据集的维度只是人为的高。
2.2.1. 介绍#
多维数据集可能非常难以可视化。 虽然可以绘制二维或三维数据来显示数据的固有结构,但等效的多维图则不那么直观。 为了帮助数据集结构的可视化,必须以某种方式减少维度。
实现这种维度缩减的最简单方法是对数据进行随机投影。 尽管这允许对数据结构进行一定程度的可视化,但选择的随机性还有很多不足之处。 在随机投影中,数据中更有趣的结构很可能会丢失。
数字_IMG投影_IMG
为了解决这个问题,已经设计了许多有监督和无监督的线性降维框架,例如主成分分析(PCA)、独立成分分析、线性鉴别分析等。 这些算法定义了特定的规则来选择数据的“有趣”线性投影。这些方法可能很强大,但通常会错过数据中重要的非线性结构。
PCA_IMG LDA_IMG
Manifold Learning可以被认为是一种尝试将PCA等线性框架概括为对数据中的非线性结构敏感。尽管存在监督变体,但典型的多管学习问题是无监督的:它从数据本身学习数据的多维结构,而无需使用预定的分类。
示例
看到 手写数字的流形学习:局部线性嵌入,Isomap... 对于手写数字的降维示例。
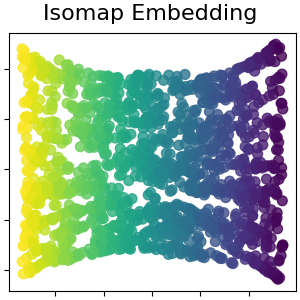
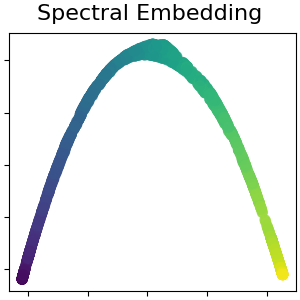
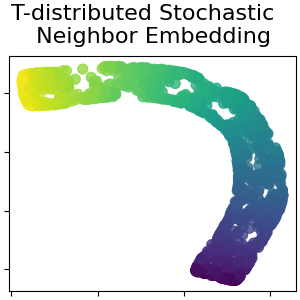
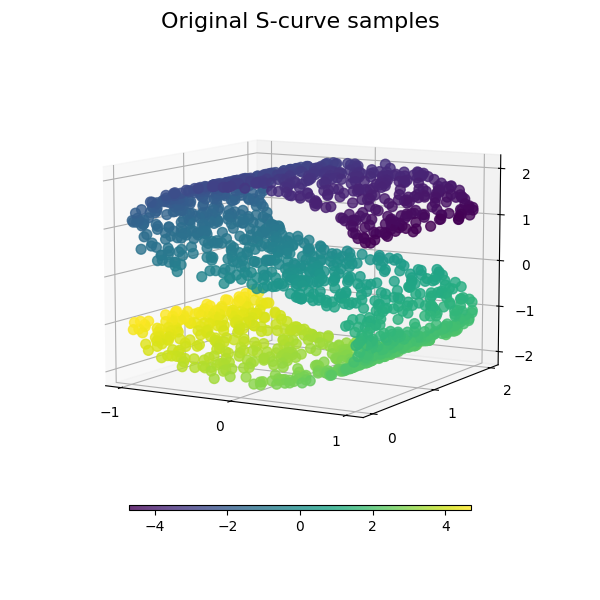
看到 多种学习方法的比较 对于玩具“S曲线”数据集的降维示例。
看到 股票市场结构可视化 例如,使用多维学习根据历史股价绘制股市结构。
看到 分割球面上的流形学习方法 这是应用于球形数据集的多维学习技术的示例。
看到 瑞士滚动和瑞士洞减少 这是在Swiss Roll数据集上使用多管学习技术的示例。
下面总结了scikit-learn中可用的多种学习实现
2.2.2. Isomap#
最早的多维学习方法之一是Isomap算法,即等距映射的缩写。 Isomap可以被视为多维缩放(SCS)或核心PCA的扩展。Isomap寻求一种低维嵌入,以保持所有点之间的测地距离。 可以对对象执行Isomap Isomap .
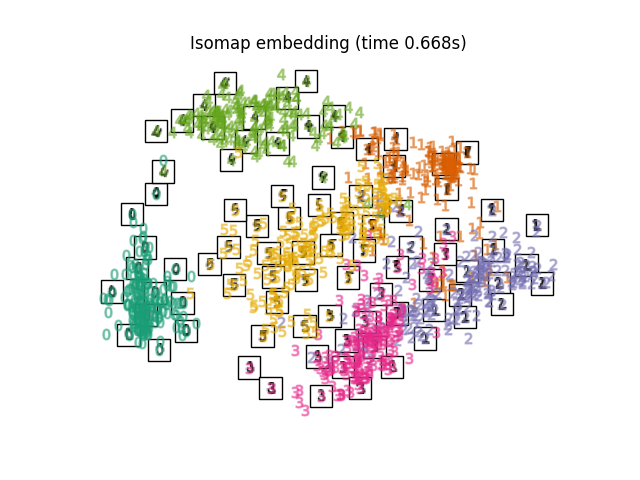
复杂性#
Isomap算法包括三个阶段:
Nearest neighbor search. Isomap使用
BallTree用于高效的邻居搜索。费用大约是 \(O[D \log(k) N \log(N)]\) ,对于 \(k\) 的最近邻居 \(N\) 点 \(D\) 尺寸.Shortest-path graph search. 已知的最有效的算法是 Dijkstra's Algorithm ,大约 \(O[N^2(k + \log(N))]\) ,或者 Floyd-Warshall algorithm ,这是 \(O[N^3]\) . 用户可以使用
path_method关键词Isomap. 如果未指定,代码将尝试为输入数据选择最佳算法。Partial eigenvalue decomposition. 嵌入被编码在与 \(d\) 最大特征值 \(N \times N\) isomap内核。 对于密集求解器,成本大约为 \(O[d N^2]\) . 通常可以使用
ARPACK解决者。 特征解算器可以由用户使用eigen_solver关键词Isomap. 如果未指定,代码将尝试为输入数据选择最佳算法。
Isomap的总体复杂性是 \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
"A global geometric framework for nonlinear dimensionality reduction" Tenenbaum,JB;德席尔瓦,V.; &兰福德,JC 科学290(5500)
2.2.3. 局部线性嵌入#
局部线性嵌入(LLE)寻求数据的低维投影,以保留局部邻近区域内的距离。 它可以被认为是一系列局部主成分分析,对其进行全球比较以找到最佳非线性嵌入。
Locally linear embedding can be performed with function
locally_linear_embedding or its object-oriented counterpart
LocallyLinearEmbedding.
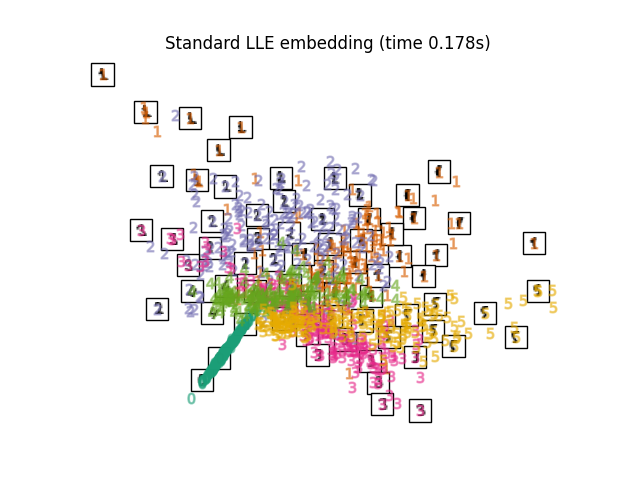
复杂性#
标准LLE算法包括三个阶段:
Nearest Neighbors Search . 请参阅上面Isomap下的讨论。
Weight Matrix Construction . \(O[D N k^3]\) . LLE权重矩阵的构建涉及一个 \(k \times k\) 线性方程,每个 \(N\) 当地社区。
Partial Eigenvalue Decomposition .请参阅上面Isomap下的讨论。
标准LLE的总体复杂性是 \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
"Nonlinear dimensionality reduction by locally linear embedding" Roweis,S. & Saul,L. 科学290:2323(2000)
2.2.4. 改进的局部线性嵌入#
LLE的一个众所周知的问题是正则化问题。 当邻域的数目大于输入维数时,定义每个局部邻域的矩阵是秩亏的。 为了解决这个问题,标准LLE应用任意正规化参数 \(r\) ,它是相对于局部权重矩阵的轨迹选择的。 尽管可以正式表明,作为 \(r \to 0\) ,解决方案收敛到所需的嵌入,则不能保证找到最佳解决方案 \(r > 0\) . 这个问题体现在扭曲了管汇的基本几何形状的嵌入中。
One method to address the regularization problem is to use multiple weight
vectors in each neighborhood. This is the essence of modified locally
linear embedding (MLLE). MLLE can be performed with function
locally_linear_embedding or its object-oriented counterpart
LocallyLinearEmbedding, with the keyword method = 'modified'.
It requires n_neighbors > n_components.
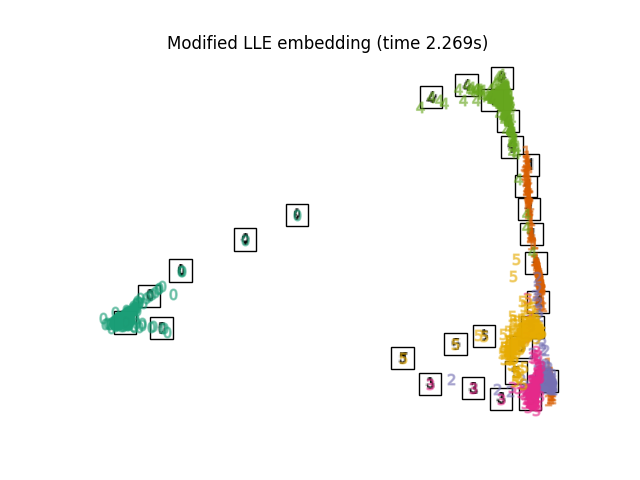
复杂性#
MLLE算法包括三个阶段:
Nearest Neighbors Search . 与标准LLE相同
Weight Matrix Construction .约 \(O[D N k^3] + O[N (k-D) k^2]\) . 第一项完全相当于标准LLE的项。 第二项与从多个权重构建权重矩阵有关。 在实践中,与阶段1和3的成本相比,构建MLLE权重矩阵的增加成本相对较小。
Partial Eigenvalue Decomposition .与标准LLE相同
MLLE的总体复杂性是 \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
2.2.5. Hessian本征映射#
Hessian Eigenmapping (also known as Hessian-based LLE: HLLE) is another method
of solving the regularization problem of LLE. It revolves around a
hessian-based quadratic form at each neighborhood which is used to recover
the locally linear structure. Though other implementations note its poor
scaling with data size, sklearn implements some algorithmic
improvements which make its cost comparable to that of other LLE variants
for small output dimension. HLLE can be performed with function
locally_linear_embedding or its object-oriented counterpart
LocallyLinearEmbedding, with the keyword method = 'hessian'.
It requires n_neighbors > n_components * (n_components + 3) / 2.
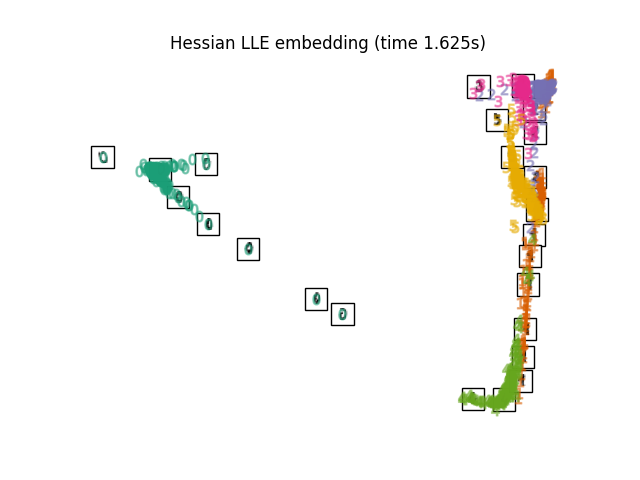
复杂性#
HLLE算法包括三个阶段:
Nearest Neighbors Search . 与标准LLE相同
Weight Matrix Construction .约 \(O[D N k^3] + O[N d^6]\) . 第一项反映了与标准LLE类似的成本。 第二项来自局部黑森估计量的QR分解。
Partial Eigenvalue Decomposition .与标准LLE相同。
标准HLLE的总体复杂性是 \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
"Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data" 多诺霍,D. & Grimes,C.美国国家科学院。100:5591(2003)
2.2.6. 光谱嵌入#
Spectral Embedding is an approach to calculating a non-linear embedding.
Scikit-learn implements Laplacian Eigenmaps, which finds a low dimensional
representation of the data using a spectral decomposition of the graph
Laplacian. The graph generated can be considered as a discrete approximation of
the low dimensional manifold in the high dimensional space. Minimization of a
cost function based on the graph ensures that points close to each other on
the manifold are mapped close to each other in the low dimensional space,
preserving local distances. Spectral embedding can be performed with the
function spectral_embedding or its object-oriented counterpart
SpectralEmbedding.
复杂性#
谱嵌入(拉普拉斯特征映射)算法包括三个阶段:
Weighted Graph Construction .使用亲和力(邻近)矩阵表示将原始输入数据转换为图形表示。
Graph Laplacian Construction .非正规化图拉普拉斯构造为 \(L = D - A\) 对于并标准化为 \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\) .
Partial Eigenvalue Decomposition .特征值分解是在拉普拉斯图上完成的。
谱嵌入的总体复杂性是 \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
"Laplacian Eigenmaps for Dimensionality Reduction and Data Representation" M.贝尔金,P. Niyogi,神经计算,2003年6月; 15(6):1373-1396
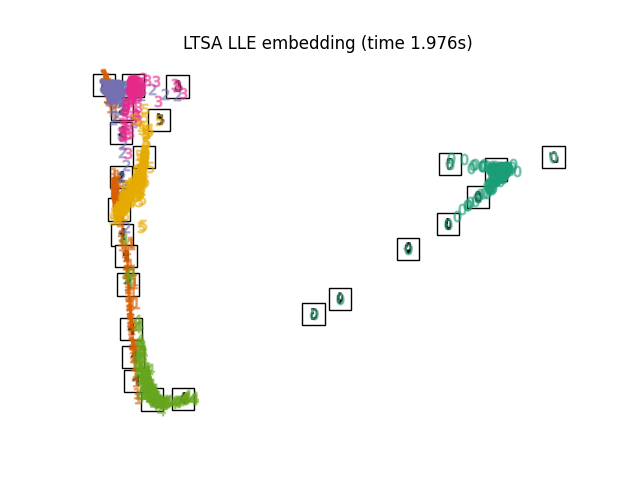
2.2.7. Local Tangent Space Alignment#
Though not technically a variant of LLE, Local tangent space alignment (LTSA)
is algorithmically similar enough to LLE that it can be put in this category.
Rather than focusing on preserving neighborhood distances as in LLE, LTSA
seeks to characterize the local geometry at each neighborhood via its
tangent space, and performs a global optimization to align these local
tangent spaces to learn the embedding. LTSA can be performed with function
locally_linear_embedding or its object-oriented counterpart
LocallyLinearEmbedding, with the keyword method = 'ltsa'.
复杂性#
LTSA算法包括三个阶段:
Nearest Neighbors Search . 与标准LLE相同
Weight Matrix Construction .约 \(O[D N k^3] + O[k^2 d]\) . 第一项反映了与标准LLE类似的成本。
Partial Eigenvalue Decomposition .与标准LLE相同
标准LTSA的总体复杂性是 \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\) .
\(N\) :训练数据点数量
\(D\) :输入维度
\(k\) :最近邻居的数量
\(d\) :输出维度
引用
"Principal manifolds and nonlinear dimensionality reduction via tangent space alignment" 张,Z。&查,H.上海大学学刊8:406(2004)
2.2.8. 多维缩放(SCS)#
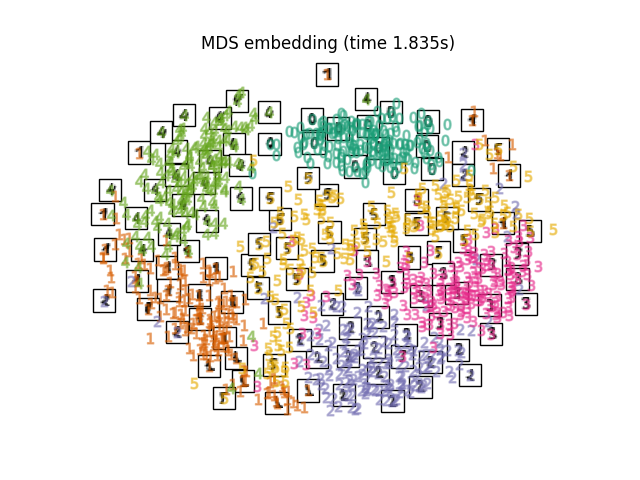
Multidimensional scaling (MDS )寻求数据的低维表示,其中距离很好地尊重原始多维空间中的距离。
总的来说, MDS 是一种用于分析不同数据的技术。它试图将差异建模为欧几里得空间中的距离。这些数据可以是物体之间的相似度评级、分子的相互作用频率或国家之间的贸易指数。
有两种类型的DDS算法:度量算法和非度量算法。在scikit-learn中,班级 MDS 实现两者。在度量BDS中,嵌入空间中的距离被设置为尽可能接近相异度数据。在非度量版本中,该算法将尝试保持距离的顺序,从而寻求嵌入空间中的距离与输入差异之间的单调关系。
Let \(\delta_{ij}\) be the dissimilarity matrix between the \(n\) input points (possibly arising as some pairwise distances \(d_{ij}(X)\) between the coordinates \(X\) of the input points). Disparities \(\hat{d}_{ij} = f(\delta_{ij})\) are some transformation of the dissimilarities. The MDS objective, called the raw stress, is then defined by \(\sum_{i < j} (\hat{d}_{ij} - d_{ij}(Z))^2\), where \(d_{ij}(Z)\) are the pairwise distances between the coordinates \(Z\) of the embedded points.
非指标型点石成金#
Non metric MDS focuses on the ordination of the data. If
\(\delta_{ij} > \delta_{kl}\), then the embedding
seeks to enforce \(d_{ij}(Z) > d_{kl}(Z)\). A simple algorithm
to enforce proper ordination is to use an
isotonic regression of \(d_{ij}(Z)\) on \(\delta_{ij}\), yielding
disparities \(\hat{d}_{ij}\) that are a monotonic transformation
of dissimilarities \(\delta_{ij}\) and hence having the same ordering.
This is done repeatedly after every step of the optimization algorithm.
In order to avoid the trivial solution where all embedding points are
overlapping, the disparities \(\hat{d}_{ij}\) are normalized.
请注意,由于我们只关心相对排序,因此我们的目标应该对简单的翻译和缩放保持不变,但度量BDS中使用的压力对缩放敏感。为了解决这个问题,非指标性SCS返回标准化压力,也称为Stress-1,定义为
如果出现以下情况,则返回标准化压力-1 normalized_stress=True .

引用
"More on Multidimensional Scaling and Unfolding in R: smacof Version 2" Mair P,Groenen P.,de Leeuw J.统计软件杂志(2022)
"Modern Multidimensional Scaling - Theory and Applications" 博格岛; Groenen P. Springer统计学系列(1997)
"Nonmetric multidimensional scaling: a numerical method" Kruskal,J. Psychmetrika,29(1964)
"Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis" Kruskal,J. Psychmetrika,29,(1964)
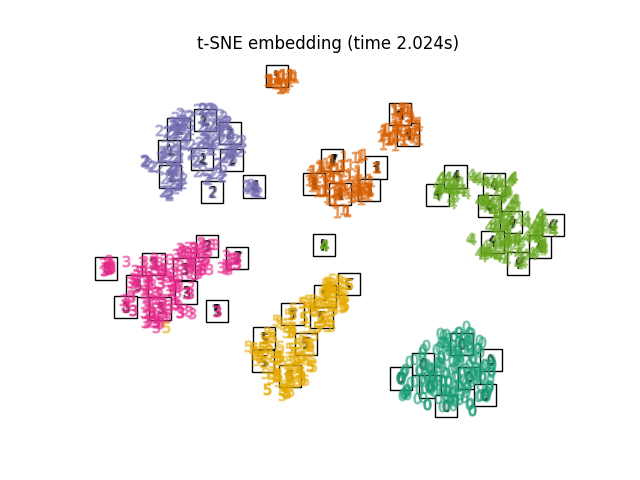
2.2.9. t-分布随机邻居嵌入(t-SNE)#
t-SNE (TSNE )将数据点的亲和力转换为概率。原始空间中的亲和力由高斯联合概率表示,嵌入空间中的亲和力由Student t分布表示。这使得t-SNE对局部结构特别敏感,并且与现有技术相比具有一些其他优势:
在一张地图上揭示多种比例的结构
揭示位于多个不同的集合或集群中的数据
减少将点集中在中心的倾向
虽然Isomap、LLE和变体最适合展开单个连续低维多边形,但t-SNE将专注于数据的局部结构,并倾向于提取聚集的局部样本组,如S曲线示例中突出显示的。这种基于局部结构对样本进行分组的能力可能有利于在视觉上理清同时包含多个流管的数据集,就像数字数据集的情况一样。
原始空间和嵌入空间中联合概率的Kullback-Leibler(KL)偏差将通过梯度下降最小化。请注意,KL分歧不是凸的,即具有不同初始化的多次重新启动将最终达到KL分歧的局部最小值。因此,有时尝试不同的种子并选择KL分歧最低的嵌入是有用的。
使用t-SNE的缺点大致有:
t-SNE的计算成本很高,并且可能需要几个小时来处理数百万个样本的数据集,而PCA将在几秒钟或几分钟内完成
Barnes-Hut t-SNE方法仅限于二维或三维嵌入。
该算法是随机的,使用不同种子的多次重新启动可以产生不同的嵌入。然而,选择错误最小的嵌入是完全合法的。
全局结构没有被明确保留。通过使用PCA初始化点(使用
init='pca').
优化t-SNE#
t-SNE的主要目的是实现多维数据的可视化。因此,当数据嵌入二维或三维时,效果最好。
优化KL分歧有时可能有点棘手。有五个参数可以控制t-SNE的优化,从而可能控制最终嵌入的质量:
困惑
早期夸张因素
学习率
最大迭代次数
角度(不用于确切方法)
The perplexity is defined as \(k=2^{(S)}\) where \(S\) is the Shannon entropy of the conditional probability distribution. The perplexity of a \(k\)-sided die is \(k\), so that \(k\) is effectively the number of nearest neighbors t-SNE considers when generating the conditional probabilities. Larger perplexities lead to more nearest neighbors and less sensitive to small structure. Conversely a lower perplexity considers a smaller number of neighbors, and thus ignores more global information in favour of the local neighborhood. As dataset sizes get larger more points will be required to get a reasonable sample of the local neighborhood, and hence larger perplexities may be required. Similarly noisier datasets will require larger perplexity values to encompass enough local neighbors to see beyond the background noise.
最大迭代次数通常足够高,不需要任何调优。优化包括两个阶段:早期夸张阶段和最终优化。在早期夸张期间,原始空间中的联合概率将通过与给定因子相乘而人为地增加。更大的因子导致数据中自然聚类之间的差距更大。如果该因素太高,KL背离可能会在此阶段增加。通常不需要调整。一个关键参数是学习率。如果太低,梯度下降将陷入不良的局部最小值。如果太高,则优化过程中KL偏差会增加。Belkina等人(2019)提出的一种启发式方法是将学习率设置为样本量除以早期夸大因子。我们将这个启发式实施为 learning_rate='auto' 论点更多技巧请参阅Laurens van der Maaten的常见问题解答(请参阅参考文献)。最后一个参数(角度)是性能和准确性之间的权衡。更大的角度意味着我们可以通过一个点来逼近更大的区域,从而导致速度更快,但结果不太准确。
"How to Use t-SNE Effectively" 提供了对各种参数影响的良好讨论,以及探索不同参数影响的交互式图。
巴内斯小屋t-SNE#
这里实现的Barnes-Hut t-SNE通常比其他多管齐学习算法慢得多。优化相当困难,梯度的计算 \(O[d N log(N)]\) ,在哪里 \(d\) 是输出维数, \(N\) 是样本数量。Barnes-Hut方法改进了t-SNE复杂性为的确切方法 \(O[d N^2]\) ,但还有其他几个显着的区别:
Barnes-Hut实现仅在目标维度为3或更小时有效。构建可视化时,2D情况是典型的。
Barnes-Hut仅适用于密集输入数据。稀疏数据矩阵只能用精确方法嵌入,或者可以通过密集的低秩投影来近似,例如使用
PCABarnes-Hut是精确方法的近似。逼近用角度参数化,因此当方法=“exact”时,角度参数未使用
Barnes-Hut的可扩展性明显更强。Barnes-Hut可用于嵌入数十万个数据点,而确切的方法可以在变得计算上棘手之前处理数千个样本
出于可视化目的(这是t-SNE的主要用例),强烈建议使用Barnes-Hut方法。精确的t-SNE方法对于检查可能在更高维空间中嵌入的理论性质很有用,但由于计算限制而局限于小数据集。
另请注意,数字标签与t-SNE找到的自然分组大致匹配,而PCA模型的线性2D投影产生了标签区域很大程度上重叠的表示。这是一个强有力的线索,表明这些数据可以通过专注于局部结构的非线性方法(例如具有高斯函数核的支持者)很好地分离。然而,未能在2D中用t-SNE可视化良好分离的均匀标记组并不一定意味着数据无法通过监督模型正确分类。情况可能是2维不够高,无法准确地表示数据的内部结构。
引用
"Visualizing High-Dimensional Data Using t-SNE" van der Maaten,LJP;辛顿,G.机器学习研究杂志(2008)
"Accelerating t-SNE using Tree-Based Algorithms" van der Maaten,LJP;《机器学习研究杂志》15(Oct):3221-3245,2014。
"Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets" 贝尔基纳,A.C.,西科莱拉,首席执行官,阿诺,R.,哈尔珀特,R.,Spidlen,J.,斯奈德-卡皮翁,J.E.,自然通讯10,5415(2019)。
2.2.10. 实际使用技巧#
确保所有要素使用相同的比例。由于多管学习方法基于最近邻搜索,否则算法可能会表现不佳。 看到 StandardScaler 用于扩展异类数据的便捷方法。
每个例程计算出的重建误差可用于选择最佳输出维度。 用于 \(d\) - 嵌入在 \(D\) - 维度参数空间,重建误差将随着
n_components增加直到n_components == d.注意,噪声数据可以“短路”流形,本质上充当流形的部分之间的桥梁,否则这些部分将被很好地分离。 噪声和/或不完整数据上的流形学习是一个活跃的研究领域。
某些输入配置可能导致奇异权重矩阵,例如当数据集中的两个以上点相同时,或者当数据被分成不相交的组时。 在这种情况下,
solver='arpack'将无法找到空空间。 解决这个问题的最简单方法是使用solver='dense'它将在奇异矩阵上工作,尽管根据输入点的数量,它可能非常慢。 或者,人们可以尝试理解奇异性的来源:如果它是由于不相交的集合,那么增加n_neighbors可能有帮助。 如果是由于数据集中的点相同,则删除这些点可能会有所帮助。
参见
完全随机树嵌入 也可以用于推导特征空间的非线性表示,但它不执行维度约简。