7.6. 随机投影#

的 sklearn.random_projection 模块实现了一种简单且计算高效的方法，通过牺牲受控的准确度（作为额外方差）来减少数据的维度，以获得更快的处理时间和更小的模型大小。该模块实现两种类型的非结构化随机矩阵： Gaussian random matrix 和 sparse random matrix .

控制随机投影矩阵的维度和分布，以保留数据集任何两个样本之间的成对距离。因此，随机投影是基于距离的方法的合适逼近技术。

引用

桑乔伊·达斯古普塔。2000. Experiments with random projection. Craig Boutilier和Moisés Goldsz（编辑）在第十六届人工智能不确定性会议论文集（UAI ' 00）中。摩根·考夫曼出版公司，美国加利福尼亚州旧金山，143-151。
艾拉·宾厄姆和海基·曼尼拉。2001. Random projection in dimensionality reduction: applications to image and text data. 第七届ACN SIGKDD知识发现和数据挖掘国际会议（KDD ' 01）会议记录。美国纽约州纽约州ACC，245-250。

7.6.1. 约翰逊-林登施特劳斯引理#

随机投影效率背后的主要理论结果是 Johnson-Lindenstrauss lemma (quoting Wikipedia) :

在数学中，约翰逊-林登施特劳斯引理是关于点从多维到低维欧几里得空间的低失真嵌入的结果。该引理指出，多维空间中的一小群点可以嵌入到低维得多的空间中，以使点之间的距离几乎保持不变。用于嵌入的地图至少是Lipschitz，甚至可以被视为一个正交投影。

仅知道样本数量， johnson_lindenstrauss_min_dim 保守估计随机子空间的最小大小，以保证随机投影引入的有界失真：：

>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
np.int64(663)
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([    663,   11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894,  9868, 11841])

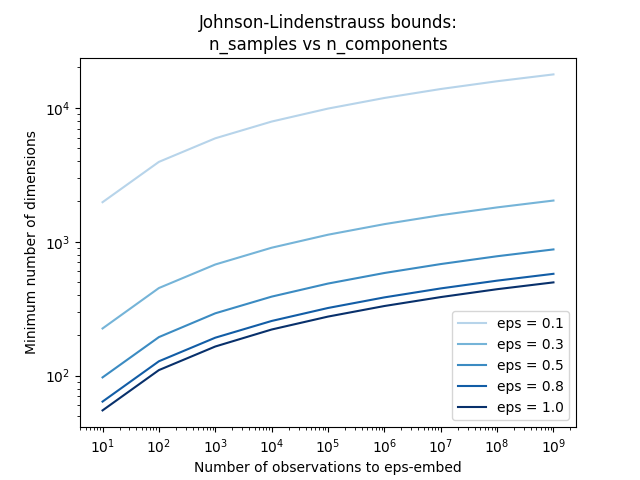
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_001.png

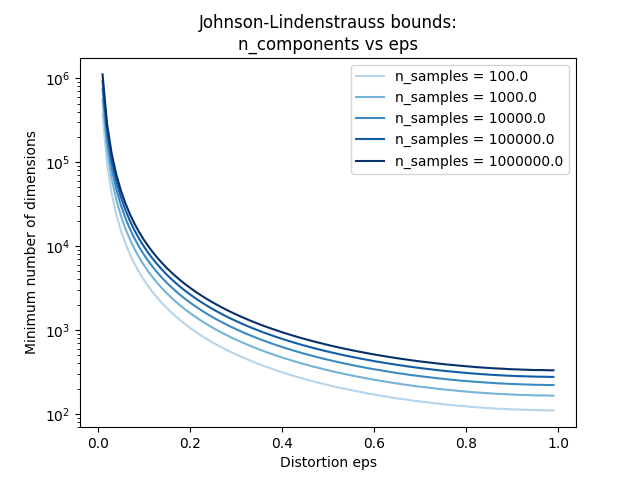
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_002.png

示例

看到随机投影嵌入的Johnson-Lindenstrauss界对约翰逊-林登施特劳斯引理进行了理论解释，并使用稀疏随机矩阵进行了经验验证。

引用

桑乔伊·达斯古普塔和阿努帕姆·古普塔，1999年。 An elementary proof of the Johnson-Lindenstrauss Lemma.

7.6.2. 高斯随机投影#

的 GaussianRandomProjection 通过将原始输入空间投影到随机生成的矩阵上来降低维度，其中分量从以下分布中提取 \(N(0, \frac{1}{n_{components}})\) .

以下是一个小摘录，说明了如何使用高斯随机投影Transformer：：

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

7.6.3. 稀疏随机投影#

的 SparseRandomProjection 通过使用稀疏随机矩阵投影原始输入空间来降低维度。

稀疏随机矩阵是稠密高斯随机投影矩阵的替代方案，可以保证类似的嵌入质量，同时具有更高的内存效率，并允许更快地计算投影数据。

如果我们定义 s = 1 / density ，随机矩阵的元素是从

\[\begin{split}\left\{ \begin{array}{c c l} -\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ 0 &\text{with probability} & 1 - 1 / s \\ +\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ \end{array} \right.\end{split}\]

哪里 \(n_{\text{components}}\) 是投影子空间的大小。默认情况下，非零元素的密度设置为Li Ping等人建议的最小密度： \(1 / \sqrt{n_{\text{features}}}\) .

以下是一个小摘录，说明了如何使用稀疏随机投影Transformer：：

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

引用

D.无眼龙2003. Database-friendly random projections: Johnson-Lindenstrauss with binary coins .计算机与系统科学杂志66（2003）671-687。
李萍、特雷弗·J·哈斯蒂和肯尼思·W教堂2006. Very sparse random projections. 第12届ACN SIGKDD知识发现和数据挖掘国际会议（KDD ' 06）会议记录。美国纽约州纽约州ACC，287-296。

7.6.4. 逆变换#

随机投影变形器有 compute_inverse_components 参数.创建随机后，设置为True components_ 矩阵在匹配过程中，Transformer计算该矩阵的伪逆并将其存储为 inverse_components_ .的 inverse_components_ 矩阵有形状 \(n_{features} \times n_{components}\) ，并且无论成分矩阵是稀疏还是稠密，它始终是稠密的矩阵。因此，根据功能和组件的数量，它可能会使用大量内存。

当 inverse_transform 方法被调用，它计算输入的积 X 以及逆分量的转置。如果在匹配期间计算了逆分量，则在每次调用时都会重复使用它们 inverse_transform .否则，每次都会重新计算它们，这可能会很昂贵。结果总是密集的，即使 X 是稀疏的

以下是一个小代码示例，说明了如何使用逆变换功能：：

>>> import numpy as np
>>> from sklearn.random_projection import SparseRandomProjection
>>> X = np.random.rand(100, 10000)
>>> transformer = SparseRandomProjection(
...   compute_inverse_components=True
... )
...
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
>>> X_new_inversed = transformer.inverse_transform(X_new)
>>> X_new_inversed.shape
(100, 10000)
>>> X_new_again = transformer.transform(X_new_inversed)
>>> np.allclose(X_new, X_new_again)
True