1.3. 核岭回归

核岭回归（KRR） [M2012] 结合 岭回归与分类 （线性最小平方 \(L_2\) - 规范正规化） kernel trick .因此，它学习由各自的内核和数据引发的空间中的线性函数。对于非线性核，这对应于原始空间中的非线性函数。

The form of the model learned by KernelRidge is identical to support vector regression (SVR). However, different loss functions are used: KRR uses squared error loss while support vector regression uses \(\epsilon\)-insensitive loss, both combined with \(L_2\) regularization. In contrast to SVR, fitting KernelRidge can be done in closed-form and is typically faster for medium-sized datasets. On the other hand, the learned model is non-sparse and thus slower than SVR, which learns a sparse model for \(\epsilon > 0\), at prediction-time.

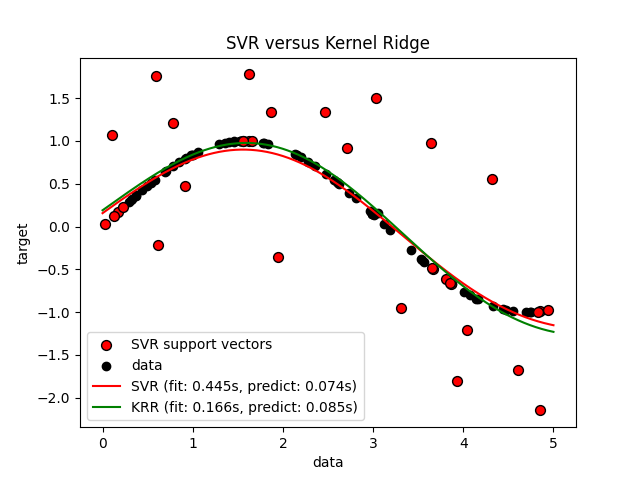
下图比较 KernelRidge 和 SVR 在人工数据集上，该数据集由一个sin目标函数和每五个数据点添加的强噪音组成。学习的模型 KernelRidge 和 SVR 绘制了图，其中使用网格搜索优化了RBS核的复杂性/正规化和带宽。学到的功能非常相似;但是，合适 KernelRidge 大约比贴合快七倍 SVR (both使用网格搜索）。然而，100，000个目标值的预测速度快了三倍多 SVR 因为它仅使用100个训练数据点中的大约1/3作为支持载体学习了稀疏模型。

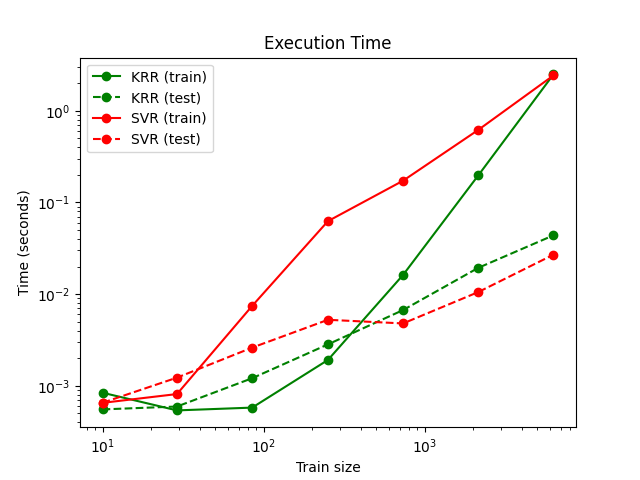
下一个图比较了适合和预测 KernelRidge 和 SVR 针对不同大小的训练集。拟合 KernelRidge 快于 SVR 对于中等规模的训练集（少于1000个样本）;但是，对于较大的训练集 SVR 规模更好。关于预测时间， SVR 快于 KernelRidge 由于学习到的稀疏解决方案，适用于所有大小的训练集。请注意，稀疏度以及预测时间取决于参数 \(\epsilon\) 和 \(C\) 的 SVR ; \(\epsilon = 0\) 将对应于密集模型。

示例

• 核岭回归与SVR的比较

引用

[M2012]

“机器学习：概率角度”墨菲，K。P. -第14.4.3章，pp。492-493，麻省理工学院出版社，2012年