1.10. 决策树#
Decision Trees (DTs) 是一种非参数监督学习方法,用于 classification 和 regression .目标是创建一个模型,通过学习从数据特征推断出的简单决策规则来预测目标变量的值。树可以被视为分段常数逼近。
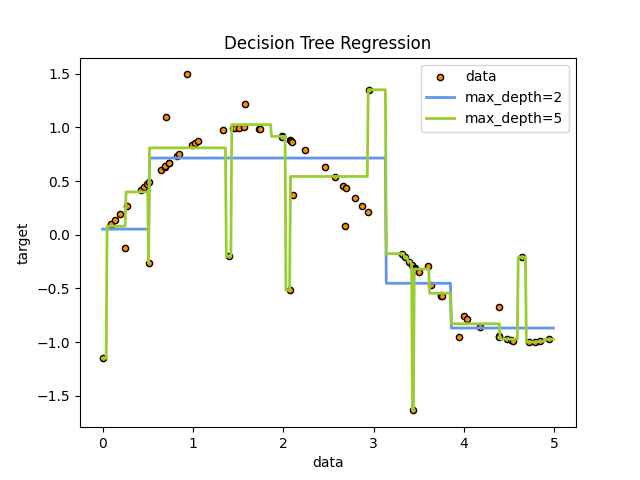
例如,在下面的示例中,决策树从数据中学习,以使用一组if-then-else决策规则来逼近一条曲线。树越深,决策规则越复杂,模型越适合。
决策树的一些优点是:
易于理解和解释。树木可以被可视化。
需要很少的数据准备。其他技术通常需要数据规范化,需要创建虚拟变量并删除空白值。一些树和算法组合支持 missing values .
使用树的成本(即,预测数据)用于训练树的数据点数量是对的。
能够处理数字和分类数据。然而,scikit-learn实现目前不支持类别变量。其他技术通常专门用于分析只有一种类型变量的数据集。看到 algorithms for more information.
能够处理多输出问题。
使用白盒模型。如果给定的情况在模型中是可观察到的,那么对该条件的解释很容易通过布尔逻辑来解释。相比之下,在黑匣子模型中(例如,在人工神经网络中),结果可能更难以解释。
可以使用统计测试来验证模型。这使得可以考虑模型的可靠性。
即使生成数据的真实模型在某种程度上违反了其假设,也能表现良好。
决策树的缺点包括:
决策树学习者可能会创建过于复杂的树,而无法很好地概括数据。这就是所谓的过度贴合。为了避免这个问题,需要修剪、设置叶节点所需的最小样本数量或设置树的最大深度等机制。
决策树可能不稳定,因为数据中的微小变化可能会导致生成完全不同的树。通过在集成中使用决策树来缓解这个问题。
决策树的预测既不是平滑的也不是连续的,而是分段恒定的逼近,如上图所示。因此,他们不善于推断。
已知学习最优决策树的问题在最优性的几个方面甚至对于简单的概念来说都是NP完全的。因此,实际的决策树学习算法基于启发式算法,例如贪婪算法,其中在每个节点处做出局部最优决策。此类算法无法保证返回全局最优决策树。 这可以通过在集成学习器中训练多棵树来缓解,其中特征和样本通过替换随机采样。
有些概念很难学习,因为决策树不容易表达它们,例如异或、宇称或多路转换器问题。
如果某些类占主导地位,决策树学习者就会创建有偏见的树。因此,建议在与决策树匹配之前平衡数据集。
1.10.1. 分类#
DecisionTreeClassifier 是能够对数据集执行多类分类的类。
与其他分类器一样, DecisionTreeClassifier 将两个数组作为输入:形状为稀疏或密集的数组X (n_samples, n_features) 保存训练样本和一个由整值、形状组成的数组Y (n_samples,) ,持有训练样本的班级标签::
>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
经过匹配后,该模型可用于预测样本类别::
>>> clf.predict([[2., 2.]])
array([1])
如果存在多个具有相同且最高概率的类别,分类器将预测这些类别中指数最低的类别。
作为输出特定类的替代方案,可以预测每个类的概率,这是叶子中该类的训练样本的比例::
>>> clf.predict_proba([[2., 2.]])
array([[0., 1.]])
DecisionTreeClassifier 能够两种二进制(其中标签是 [-1, 1] )分类和多类(标签在哪里 [0, ..., K-1] )分类。
使用Iris数据集,我们可以构建如下树:
>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)
训练后,您可以用 plot_tree 功能::
>>> tree.plot_tree(clf)
[...]
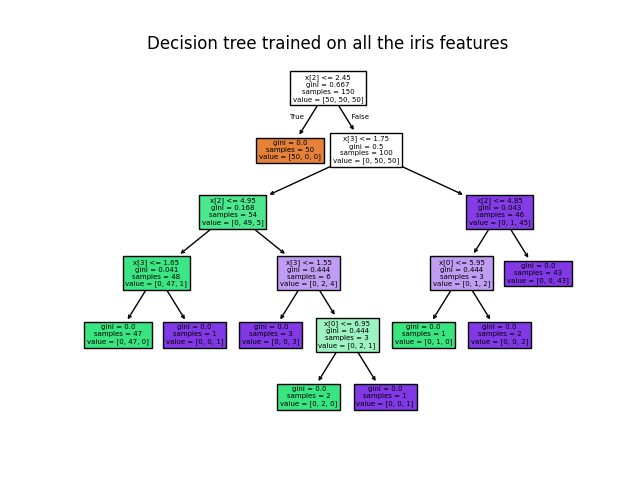
出口树木的替代方法#
我们还可以将树输出到 Graphviz 使用的格式 export_graphviz 出口商。如果使用 conda 包管理器、graphviz二进制文件和Python包可以安装在一起 conda install python-graphviz .
或者,可以从graphviz项目主页下载graphviz的二进制文件,并从pypi安装Python包装器 pip install graphviz .
以下是在整个虹膜数据集上训练的上述树的graphviz输出示例;结果保存在输出文件中 iris.pdf
>>> import graphviz
>>> dot_data = tree.export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
的 export_graphviz exjector还支持各种美学选项,包括按节点的类(或回归值)着色节点,以及根据需要使用显式变量和类名称。Deliveryter笔记本还会自动在线渲染这些图::
>>> dot_data = tree.export_graphviz(clf, out_file=None,
... feature_names=iris.feature_names,
... class_names=iris.target_names,
... filled=True, rounded=True,
... special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
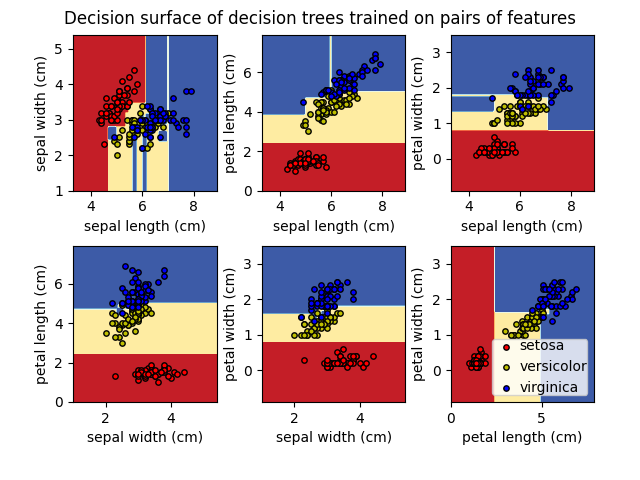
或者,也可以使用该函数以文本格式输出树 export_text .此方法不需要安装外部库,并且更加紧凑:
>>> from sklearn.datasets import load_iris
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2)
>>> decision_tree = decision_tree.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
| |--- class: 0
|--- petal width (cm) > 0.80
| |--- petal width (cm) <= 1.75
| | |--- class: 1
| |--- petal width (cm) > 1.75
| | |--- class: 2
示例
1.10.2. 回归#

决策树还可以应用于回归问题,使用 DecisionTreeRegressor 课
与分类设置中一样,fit方法将采用数组X和y作为参数,只是在这种情况下,y预计具有浮点值而不是整值::
>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
示例
1.10.3. 多输出问题#
多输出问题是一个有多个输出需要预测的监督学习问题,即当Y是2d形状数组时 (n_samples, n_outputs) .
当输出之间没有相关性时,解决此类问题的一个非常简单的方法是构建n个独立的模型,即每个输出一个模型,然后使用这些模型独立预测n个输出中的每一个。然而,由于与同一输入相关的输出值本身可能是相关的,因此通常更好的方法是构建能够同时预测所有n个输出的单个模型。首先,它需要更少的训练时间,因为只构建了一个估计器。其次,所得估计器的概括准确性通常可能会增加。
对于决策树,该策略可以很容易地用于支持多输出问题。这需要进行以下更改:
将n个输出值存储在叶子中,而不是1;
使用拆分标准计算所有n个输出的平均减少。
本模块通过在以下两种环境中实施此策略,为多输出问题提供支持 DecisionTreeClassifier 和 DecisionTreeRegressor .如果决策树适合形状的输出数组Y (n_samples, n_outputs) 那么得到的估计器将:
输出n_输出值
predict;在以下时间输出类概率的n_select数组列表
predict_proba.
中演示了使用多输出树进行回归 决策树回归 .在本例中,输入X是单个实值,输出Y是X的sin和cos。
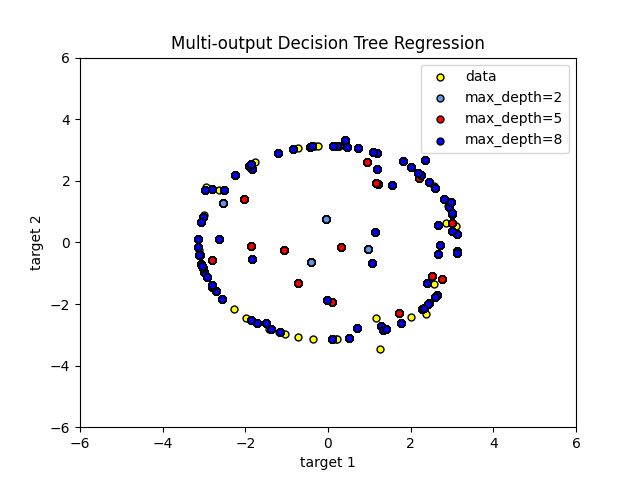
中演示了使用多输出树进行分类 使用多输出估计器完成面 .在本例中,输入X是面部上半部分的像素,输出Y是这些面部下半部分的像素。

示例
引用
M.杜蒙等人, Fast multi-class image annotation with random subwindows and multiple output randomized trees ,2009年国际计算机视觉理论与应用会议
1.10.4. 复杂性#
In general, the run time cost to construct a balanced binary tree is \(O(n_{samples}n_{features}\log(n_{samples}))\) and query time \(O(\log(n_{samples}))\). Although the tree construction algorithm attempts to generate balanced trees, they will not always be balanced. Assuming that the subtrees remain approximately balanced, the cost at each node consists of searching through \(O(n_{features})\) to find the feature that offers the largest reduction in the impurity criterion, e.g. log loss (which is equivalent to an information gain). This has a cost of \(O(n_{features}n_{samples}\log(n_{samples}))\) at each node, leading to a total cost over the entire trees (by summing the cost at each node) of \(O(n_{features}n_{samples}^{2}\log(n_{samples}))\).
1.10.5. 实际使用技巧#
决策树往往会过度适应具有大量特征的数据。获得正确的样本与特征数量的比例非常重要,因为在多维空间中样本很少的树很可能会过适应。
了解决策树结构 将有助于获得更多关于决策树如何进行预测的见解,这对于理解数据中的重要特征非常重要。
在训练时使用
export功能 使用max_depth=3作为初始树深度,以了解树如何适合您的数据,然后增加深度。请记住,树每增加一层,填充树所需的样本数量就增加一倍。 使用
max_depth控制树木的大小以防止过度贴合。使用
min_samples_split或min_samples_leaf通过控制将考虑哪些拆分,确保多个样本告知树中的每个决策。非常小的数字通常意味着树将过度适应,而大量将阻止树学习数据。尝试min_samples_leaf=5作为初始值。如果样本大小变化很大,则可以在这两个参数中使用浮点数作为百分比。而min_samples_split可以创造任意小的叶子,min_samples_leaf保证每个叶节点具有最小大小,避免回归问题中的低方差、过拟合叶节点。 对于类别较少的分类,min_samples_leaf=1往往是最好的选择。注意
min_samples_split直接且独立地考虑样本sample_weight,如果提供的话(例如,具有m个加权样本的节点仍然被视为具有恰好m个样本)。考虑min_weight_fraction_leaf或min_impurity_decrease如果需要在拆分时考虑样本权重。在训练前平衡您的数据集,以防止树偏向占主导地位的类。类别平衡可以通过从每个类别中抽样相等数量的样本来完成,或者最好通过对样本权重的总和进行标准化 (
sample_weight)对于每个类来说都是相同的值。另请注意,基于权重的预修剪标准,例如min_weight_fraction_leaf那么,与不知道样本权重的标准相比,对主导类别的偏见较小,例如min_samples_leaf.如果对样本进行加权,则使用基于权重的预修剪标准(例如
min_weight_fraction_leaf,这确保叶节点至少包含样本权重总和的一小部分。所有决策树都使用
np.float32内部阵列。如果训练数据不采用此格式,则将创建数据集的副本。如果输入矩阵X非常稀疏,建议转换为稀疏
csc_matrix在呼吁健康和稀疏之前csr_matrix在打电话预测之前。当特征在大多数样本中为零值时,稀疏矩阵输入的训练时间可能比密集矩阵快几个数量级。
1.10.6. 树算法:ID 3、C4.5、C5.0和CART#
各种决策树算法都有哪些?它们之间有何不同?哪个是在scikit-learn中实现的?
各种决策树算法#
ID3 (迭代二分法3)由Ross Quinlan于1986年开发。该算法创建一个多路树,为每个节点(即以贪婪的方式)寻找将为分类目标产生最大信息收益的分类特征。树木生长到最大大小,然后通常会应用修剪步骤来提高树木概括为不可见数据的能力。
C4.5是ID 3的后继者,通过动态定义离散属性(基于数字变量),该属性将连续属性值划分为离散的间隔集,消除了特征必须是分类的限制。C4.5将训练过的树(即ID 3算法的输出)转换为if-then规则集。然后评估每条规则的准确性,以确定它们的应用顺序。如果在没有规则的情况下规则的准确性会提高,则通过删除规则的先决条件来完成修剪。
C5.0是Quinlan在专有许可下发布的最新版本。与C4.5相比,它使用的内存更少,构建的规则集更小,同时更准确。
CART(分类和回归树)与C4.5非常相似,但不同之处在于它支持数字目标变量(回归)并且不计算规则集。CART使用在每个节点产生最大信息收益的特征和阈值来构建二元树。
scikit-learn使用CART算法的优化版本;但是,scikit-learn实现目前不支持类别变量。
1.10.7. 数学公式#
给定训练载体 \(x_i \in R^n\) ,i=1,.,l和标签载体 \(y \in R^l\) ,决策树对特征空间进行迭代划分,以便将具有相同标签或相似目标值的样本分组在一起。
Let the data at node \(m\) be represented by \(Q_m\) with \(n_m\) samples. For each candidate split \(\theta = (j, t_m)\) consisting of a feature \(j\) and threshold \(t_m\), partition the data into \(Q_m^{left}(\theta)\) and \(Q_m^{right}(\theta)\) subsets
候选节点拆分的质量 \(m\) 然后使用杂质函数或损失函数计算 \(H()\) ,选择哪个取决于正在解决的任务(分类或回归)
选择最大限度减少杂质的参数
子集的回归 \(Q_m^{left}(\theta^*)\) 和 \(Q_m^{right}(\theta^*)\) 直到达到最大允许深度, \(n_m < \min_{samples}\) 或 \(n_m = 1\) .
1.10.7.1. 分类标准#
如果目标是值为0,1,.,的分类结果K-1,用于节点 \(m\) ,让
是节点中k类观察的比例 \(m\) .如果 \(m\) 是终端节点, predict_proba 此区域的设置为 \(p_{mk}\) .杂质的常见测量方法如下。
吉尼:
对数损失或熵:
香农熵#
信息量准则计算可能类别的香农信息量。它采用到达给定叶子的训练数据点的类频率 \(m\) 作为他们的可能性。使用 Shannon entropy as tree node splitting criterion is equivalent to minimizing the log loss (also称为交叉熵和多项偏差)真实标签之间 \(y_i\) 以及概率预测 \(T_k(x_i)\) 树形模型的 \(T\) 上课 \(k\) .
要了解这一点,首先回想一下树模型的日志丢失 \(T\) 在数据集上计算 \(D\) 定义如下:
哪里 \(D\) 是训练数据集 \(n\) 对 \((x_i, y_i)\) .
在分类树中,叶节点内的预测类别概率是恒定的,即:对于所有 \((x_i, y_i) \in Q_m\) ,其中一个有: \(T_k(x_i) = p_{mk}\) 为每个类 \(k\) .
该属性使得重写成为可能 \(\mathrm{LL}(D, T)\) 作为为每个叶计算的香农熵的和, \(T\) 按到达每片叶子的训练数据点数量加权:
1.10.7.2. 回归标准#
如果目标是连续值,那么对于节点 \(m\) ,确定未来拆分位置的常见标准是均方误差(SSE或L2误差)、Poisson偏差以及平均绝对误差(MAE或L1误差)。均方差和Poisson偏差都将终端节点的预测值设置为学习的平均值 \(\bar{y}_m\) 而MAE将终端节点的预测值设置为中位数 \(median(y)_m\) .
均方误差:
平均Poisson偏差:
设置 criterion="poisson" 如果您的目标是计数或频率(每个单位的计数),这可能是一个不错的选择。无论如何, \(y >= 0\) 是使用这一标准的必要条件。请注意,它的适应速度比SSE标准慢得多。出于性能原因,实际实现会最小化半均值Poisson偏差,即平均Poisson偏差除以2。
平均绝对误差:
请注意,它的适应速度比SSE标准慢得多。
1.10.8. 缺失的价值观支持#
DecisionTreeClassifier , DecisionTreeRegressor 内置支持缺失值,使用 splitter='best' ,其中分裂是以贪婪的方式确定的。 ExtraTreeClassifier ,而且 ExtraTreeRegressor 对缺失值有内置支持 splitter='random' ,其中分裂是随机确定的。有关拆分器在非缺失值上的差异的更多详细信息,请参阅 Forest section .
存在缺失值时支持的标准是 'gini' , 'entropy' ,或者 'log_loss' ,用于分类或 'squared_error' , 'friedman_mse' ,或者 'poisson' 用于回归。
首先我们将描述如何 DecisionTreeClassifier , DecisionTreeRegressor 处理数据中的缺失值。
对于非缺失数据上的每个潜在阈值,拆分器将评估将所有缺失值转移到左节点或右节点的拆分。
决定如下:
默认情况下,预测时,具有缺失值的样本将使用训练期间发现的拆分中使用的类进行分类:
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([0, 1, 6, np.nan]).reshape(-1, 1) >>> y = [0, 0, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> tree.predict(X) array([0, 0, 1, 1])
如果两个节点的标准评估相同,则通过前往正确的节点来打破预测时缺失值的领带。拆分器还检查拆分,其中所有缺失的值都流向一个子级,非缺失的值都流向另一个子级::
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([np.nan, -1, np.nan, 1]).reshape(-1, 1) >>> y = [0, 0, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> X_test = np.array([np.nan]).reshape(-1, 1) >>> tree.predict(X_test) array([1])
如果在给定特征的训练期间没有看到缺失值,则在预测期间,缺失值将被映射到具有最多样本的孩子::
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([0, 1, 2, 3]).reshape(-1, 1) >>> y = [0, 1, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> X_test = np.array([np.nan]).reshape(-1, 1) >>> tree.predict(X_test) array([1])
ExtraTreeClassifier ,而且 ExtraTreeRegressor 处理缺失值的方式略有不同。在分割节点时,会随机选择一个阈值来分割非缺失值,然后根据随机选择的阈值将非缺失值发送到左子节点和右子节点,而缺失值也会随机发送到左子节点或右子节点。对于在每次拆分时考虑的每个特征重复此操作。选择其中最好的一种。
在预测过程中,丢失值的处理与决策树的处理相同:
默认情况下,预测时,具有缺失值的样本将使用训练期间发现的分裂中使用的类别进行分类。
如果在给定特征的训练期间没有看到缺失值,则在预测期间,缺失值将被映射到具有最多样本的孩子。
1.10.9. 最小成本复杂性修剪#
最小成本复杂性修剪是一种用于修剪树以避免过度匹配的算法,在第3章中描述 [BRE]. 该算法由以下参数化: \(\alpha\ge0\) 称为复杂性参数。复杂性参数用于定义成本复杂性衡量, \(R_\alpha(T)\) 一棵给定的树 \(T\) :
哪里 \(|\widetilde{T}|\) 是中的终端节点数量 \(T\) 和 \(R(T)\) 传统上定义为终端节点的总误分类率。或者,scikit-learn使用末端节点的总样本加权杂质 \(R(T)\) .如上所示,节点的杂质取决于标准。最小成本复杂性修剪找到的子树 \(T\) 最小化 \(R_\alpha(T)\) .
The cost complexity measure of a single node is
\(R_\alpha(t)=R(t)+\alpha\). The branch, \(T_t\), is defined to be a
tree where node \(t\) is its root. In general, the impurity of a node
is greater than the sum of impurities of its terminal nodes,
\(R(T_t)<R(t)\). However, the cost complexity measure of a node,
\(t\), and its branch, \(T_t\), can be equal depending on
\(\alpha\). We define the effective \(\alpha\) of a node to be the
value where they are equal, \(R_\alpha(T_t)=R_\alpha(t)\) or
\(\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}\). A non-terminal node
with the smallest value of \(\alpha_{eff}\) is the weakest link and will
be pruned. This process stops when the pruned tree's minimal
\(\alpha_{eff}\) is greater than the ccp_alpha parameter.
示例
引用
L.布莱曼,J·弗里德曼,R.奥尔申和C.史东.分类和回归树。沃兹沃思,贝尔蒙特,加利福尼亚州,1984年。
J.R.昆兰。C4. 5:机器学习程序。摩根·考夫曼,1993年。
T.哈斯蒂河蒂布什拉尼和J·弗里德曼。统计学习要素,施普林格,2009年。
