2.3. 聚类#

Clustering 可以使用模块执行未标记数据 sklearn.cluster .

每个集群算法有两个变体：一个类，它实现 fit 学习火车数据上的集群的方法，以及一个函数，在给定火车数据时，该函数返回与不同集群相对应的整组标签。对于班级，训练数据上的标签可以在 labels_ 属性

2.3.1. 集群方法概述#

../_images/sphx_glr_plot_cluster_comparison_001.png — scikit-learn中聚类算法的比较#

方法名称	参数	扩展性	用例	几何形状（使用公制）
K-Means	聚类数	非常大 `n_samples` 、中等 `n_clusters` 与 MiniBatch code	通用，均匀的簇大小，扁平的几何形状，不太多的簇，感应	点之间的距离
Affinity propagation	衰减、样本偏好	无法使用n_samples进行扩展	集群多、集群大小不均匀、几何形状不平坦、感性	图距离（例如最近邻图）
Mean-shift	带宽	不可扩展 `n_samples`	集群多、集群大小不均匀、几何形状不平坦、感性	点之间的距离
Spectral clustering	聚类数	介质 `n_samples` ，小的 `n_clusters`	很少的集群，甚至集群大小，非平坦的几何形状，可转换的	图距离（例如最近邻图）
Ward hierarchical clustering	集群数量或距离阈值	大 `n_samples` 和 `n_clusters`	许多集群，可能是连接性限制，可转换的	点之间的距离
Agglomerative clustering	聚类数或距离阈值、链接类型、距离	大 `n_samples` 和 `n_clusters`	许多聚类，可能是连接性约束，非欧几里德距离，	任何成对距离
DBSCAN	邻域大小	非常大 `n_samples` 、中等 `n_clusters`	非平坦几何形状、不均匀的集群大小、离群值去除、转换	最近点之间的距离
HDBSCAN	最小聚类成员，最小点邻居	大 `n_samples` 、中等 `n_clusters`	非平坦几何结构、不均匀的集群大小、离群点去除、转换、分层、可变的集群密度	最近点之间的距离
OPTICS	最小聚类成员数	非常大 `n_samples` ，大 `n_clusters`	非平坦几何形状、不均匀的集群大小、可变的集群密度、离群值去除、转换	点之间的距离
Gaussian mixtures	许多	不可扩展	扁平几何形状，适合密度估计，感性	马哈拉诺比斯与中心的距离
BIRCH	分支因子、阈值、可选的全局集群。	大 `n_clusters` 和 `n_samples`	大型数据集、离群值删除、数据简化、归纳	点之间的欧几里得距离
Bisecting K-Means	聚类数	非常大 `n_samples` 、中等 `n_clusters`	通用、均匀的集群大小、平坦的几何形状、没有空集群、归纳、分层	点之间的距离

当集群具有特定形状（即非平坦多管）并且标准欧几里得距离不是正确的度量时，非平坦几何集群很有用。这种情况出现在上图的顶部两行。

中描述了用于聚类的高斯混合模型， another chapter of the documentation 致力于混合模型。KMeans可以被视为高斯混合模型的特例，每个分量的协方差相等。

Transductive 集群方法（与 inductive 集群方法）并不是为了应用于新的、不可见的数据而设计的。

示例

归纳集群：用于处理新数据的归纳集群模型的示例。

2.3.2. K-means#

的 KMeans 算法通过尝试将样本分成n个方差相等的组来聚类数据，最小化称为 inertia 或群内平方和（见下文）。此算法需要指定集群的数量。它可以很好地扩展到大量样本，并已用于许多不同领域的广泛应用领域。

k-means算法划分一组 \(N\) 样品 \(X\) 成 \(K\) 不相交的聚类 \(C\) ，每个都用平均值来描述 \(\mu_j\) 集群中样本的数量。这些平均值通常被称为集群“重心”;请注意，一般来说，它们不是来自 \(X\) ，尽管他们生活在同一个空间。

K-means算法旨在选择最小化 inertia ，或者 within-cluster sum-of-squares criterion :

\[\sum_{i=0}^{n}\min_{\mu_j \in C}(||x_i - \mu_j||^2)\]

惯性可以被认为是衡量集群内部一致性程度的指标。它存在各种缺点：

惯性假设集群是凸的且各向同性的，但事实并非总是如此。它对细长的集群或形状不规则的多管齐反应较差。
惯性不是一个标准化指标：我们只知道越小的值越好，零是最佳的。但在非常高维度的空间中，欧几里得距离往往会变得膨胀（这是所谓的“维度诅咒”的一个例子）。运行降维算法，例如主成分分析（PCA）在k均值集群之前可以缓解这个问题并加速计算。

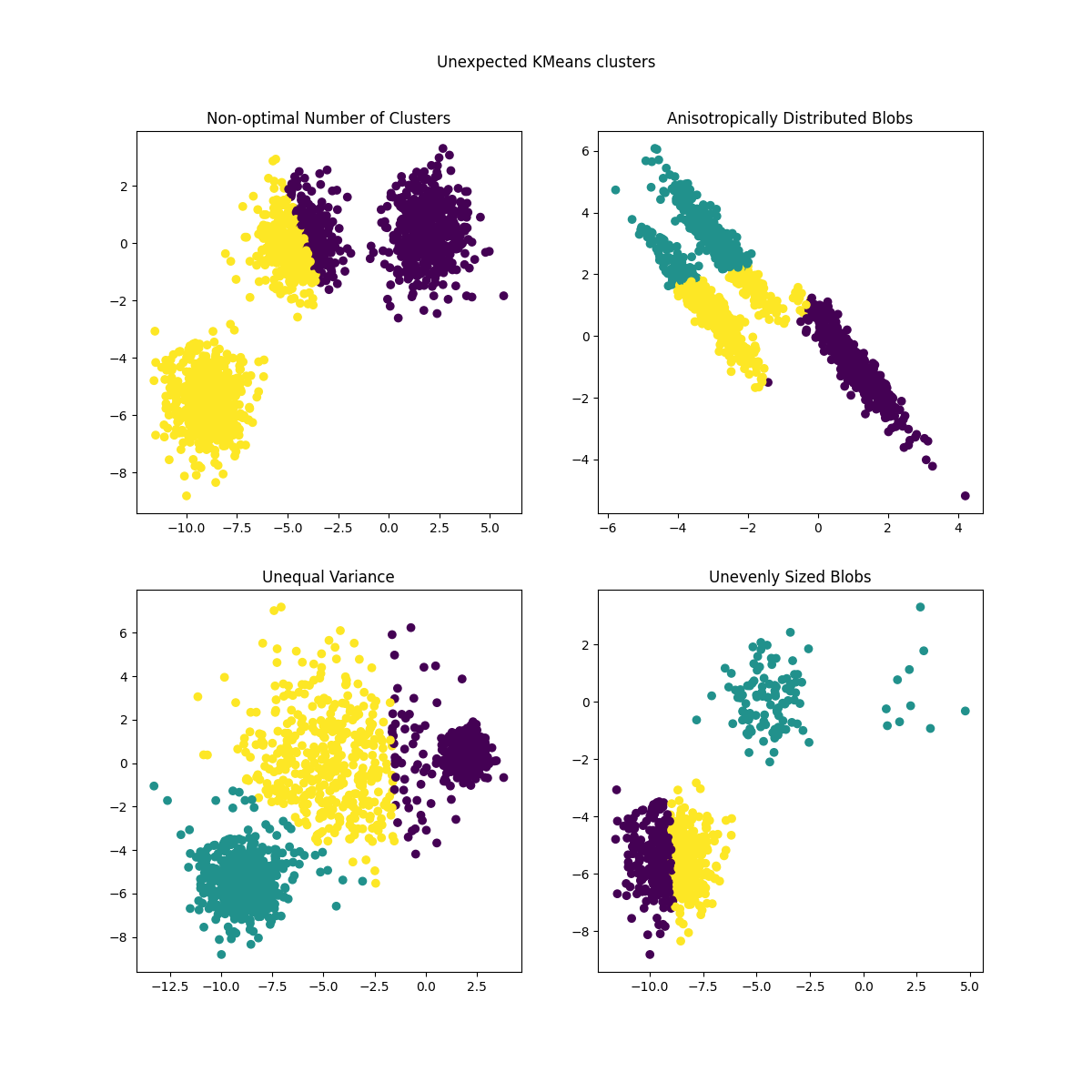
../_images/sphx_glr_plot_kmeans_assumptions_002.png

有关上述问题以及如何解决这些问题的更详细描述，请参阅示例 k均值假设的证明和在KMeans聚类中使用轮廓分析选择聚类数 .

K均值通常被称为劳埃德算法。基本上，该算法有三个步骤。第一步选择初始重心，最基本的方法是选择 \(k\) 数据集中的样本 \(X\) .初始化后，K-means包括在其他两个步骤之间循环。第一步将每个样本分配到其最近的重心。第二步通过取分配给每个先前重心的所有样本的平均值来创建新的重心。计算旧的和新的重心之间的差，算法重复这最后两个步骤，直到该值小于阈值。换句话说，它重复直到质心不显著移动。

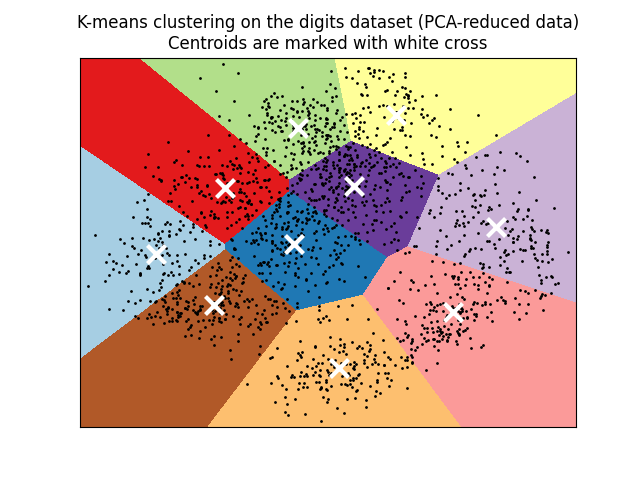
../_images/sphx_glr_plot_kmeans_digits_001.png

K-means相当于具有小的、完全相等的对角协方差矩阵的期望最大化算法。

该算法也可以通过以下概念来理解 Voronoi diagrams .首先，使用当前重心计算点的Voronoi图。沃罗诺伊图中的每个段都成为一个单独的集群。其次，将重心更新为每个分段的平均值。然后算法重复此操作，直到满足停止标准。通常，当迭代之间目标函数的相对减少小于给定容差值时，算法就会停止。在此实现中情况并非如此：当重心移动小于容差时，迭代就会停止。

如果有足够的时间，K均值将始终收敛，但这可能是局部最小值。这高度依赖于重心的初始化。因此，计算通常要进行多次，并对重心进行不同的初始化。帮助解决此问题的一种方法是k-means++初始化方案，该方案已在scikit-learn中实现（使用 init='k-means++' 参数）。这会使重心（通常）彼此远离，从而可能比随机初始化更好的结果，如参考文献中所示。有关比较不同初始化方案的详细示例，请参阅手写数字数据上的K-Means集群演示和 k均值初始化影响的实证评估 .

K-means++也可以独立调用来为其他集群算法选择种子，请参阅 sklearn.cluster.kmeans_plusplus 了解详细信息和示例使用。

该算法支持样本权重，可以通过参数给出 sample_weight .这允许在计算集群中心和惯性值时为某些样本分配更多权重。例如，为样本指定权重2相当于将该样本的副本添加到数据集 \(X\) .

示例

基于k-means的文本聚类：使用文档集群 KMeans 和 MiniBatchKMeans 基于稀疏数据
K-Means++初始化的示例：使用K-means++为其他集群算法选择种子。

2.3.2.1. 低级并行#

KMeans 通过Cython从基于BEP的并行性中受益。小块数据（256个样本）是并行处理的，此外还可以减少内存占用。有关如何控制线程数的更多详细信息，请参阅我们的并行性 notes.

示例

k均值假设的证明：演示k-means何时直观地执行以及何时不执行
手写数字数据上的K-Means集群演示：聚集手写数字

2.3.2.2. 小批量K均值#

的 MiniBatchKMeans 是 KMeans 该算法使用小批量来减少计算时间，同时仍试图优化相同的目标函数。小批量是输入数据的子集，在每次训练迭代中随机采样。这些小批量极大地减少了收敛到本地解决方案所需的计算量。与缩短k均值收敛时间的其他算法相比，迷你批量k均值产生的结果通常只比标准算法稍差。

该算法在两个主要步骤之间迭代，类似于vanilla k-means。第一步， \(b\) 从数据集中随机抽取样本，形成迷你批次。然后将这些分配给最近的重心。在第二步中，更新重心。与k均值相反，这是基于每个样本进行的。对于迷你批次中的每个样本，通过获取样本和分配给该重心的所有之前样本的流平均值来更新分配的重心。这具有降低重心随时间变化率的效果。执行这些步骤，直到达到收敛或预定的迭代次数。

MiniBatchKMeans 收敛得比 KMeans ，但结果的质量降低了。实际上，这种质量差异可能相当小，如示例和引用的参考文献所示。

../_images/sphx_glr_plot_mini_batch_kmeans_001.png

示例

K-Means和MiniBatchKMeans集群算法的比较：比较 KMeans 和 MiniBatchKMeans
基于k-means的文本聚类：使用文档集群 KMeans 和 MiniBatchKMeans 基于稀疏数据
在线学习面部部分词典

2.3.3. 仿射传播#

AffinityPropagation 通过在样本对之间发送消息直到收敛来创建集群。然后使用少量样本来描述数据集，这些样本被识别为最能代表其他样本的样本。在对之间发送的消息表示一个样本是否适合成为另一个样本的样本，该样本会根据其他对的值进行更新。这种更新迭代地发生，直到收敛，此时选择最终的样本，从而给出最终的集群。

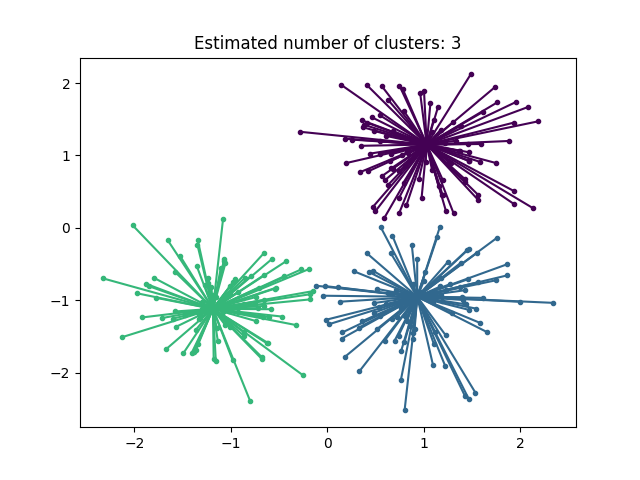
../_images/sphx_glr_plot_affinity_propagation_001.png

Affinity Propagation可能很有趣，因为它根据提供的数据选择集群的数量。为此，两个重要参数是 preference ，它控制使用的样本数量，以及 damping factor 这会抑制责任和可用性消息，以避免更新这些消息时的数字振荡。

亲和力传播的主要缺点是其复杂性。该算法具有数量级的时间复杂度 \(O(N^2 T)\) ，在哪里 \(N\) 是样本数量和 \(T\) 是收敛之前的迭代次数。此外，内存复杂性达到了 \(O(N^2)\) 如果使用密集相似性矩阵，但如果使用稀疏相似性矩阵，则可简化。这使得亲和力传播最适合中小规模的数据集。

示例

亲和力传播分簇算法演示：具有3个类别的合成2D数据集上的亲和力传播
股票市场结构可视化在金融时间序列上进行亲和传播以找到公司组

2.3.4. 均值漂移#

MeanShift 集群旨在发现 blobs 样本密度平稳。这是一种基于重心的算法，其工作原理是将重心候选更新为给定区域内点的平均值。然后在后处理阶段对这些候选项进行过滤，以消除近乎重复的，以形成最终的一组重心。

该算法自动设置聚类的数量，而不是依赖于参数 bandwidth ，它规定了要搜索的区域的大小。此参数可以手动设置，但可以使用提供的 estimate_bandwidth 函数，如果未设置带宽，则调用该函数。

该算法的可扩展性不高，因为它需要在算法执行期间进行多个最近邻搜索。算法保证收敛，但当重心变化很小时，算法将停止迭代。

通过寻找给定样本的最近重心来执行新样本的标记。

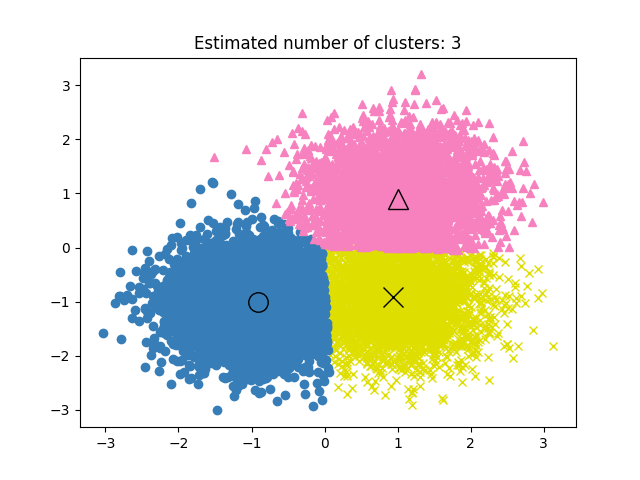
../_images/sphx_glr_plot_mean_shift_001.png

示例

均值漂移集群算法的演示：对具有3个类别的合成2D数据集进行Mean Change集群。

2.3.5. 谱聚类#

SpectralClustering 执行样本之间的亲和力矩阵的低维嵌入，然后进行集群，例如，通过KMeans，计算低维空间中特征量的分量。如果亲和力矩阵是稀疏的并且 amg solver is used for the eigenvalue problem (Note, the amg solver requires that the pyamg 模块已安装。）

当前版本的SpectralFlowering要求提前指定集群数量。它对少数集群效果良好，但不建议对许多集群使用。

对于两个集群，SpectralFlowering解决了 normalized cuts 相似性图上的问题：将图切成两半，以便与每个集群内的边的权重相比，切割的边的权重较小。当处理图像时，这个标准特别有趣，其中图的顶点是像素，并且相似性图的边缘的权重是使用图像的梯度的函数计算的。

noise_IMG segmented_IMG

警告

将距离转化为行为良好的相似性

请注意，如果相似性矩阵的值分布不均匀，例如具有负值或具有距离矩阵而不是相似性，则谱问题将是奇异的，并且该问题无法解决。在这种情况下，建议对矩阵的条目应用转换。例如，在有符号距离矩阵的情况下，通常应用热核：

similarity = np.exp(-beta * distance / distance.std())

请参阅此类应用程序的示例。

示例

用于图像分割的光谱集群：使用光谱集群将对象从嘈杂背景中分割出来。
按地区划分希腊硬币的图片：光谱集群将硬币图像分割为区域。

2.3.5.1. 不同的标签分配策略#

可以使用不同的标签分配策略，对应于 assign_labels 参数 SpectralClustering . "kmeans" 策略可以匹配更细的细节，但可能不稳定。特别是，除非你控制 random_state ，它可能无法逐运行重复，因为它依赖于随机初始化。替代 "discretize" 该策略是100%可重复的，但往往会创建相当均匀和几何形状的包裹。最近添加的 "cluster_qr" 选项是一种确定性替代方案，它倾向于在下面的示例应用程序上创建视觉上最佳的分区。

`assign_labels="kmeans"`	`assign_labels="discretize"`	`assign_labels="cluster_qr"`

2.3.5.2. 谱聚集图#

谱集群还可以用于通过其谱嵌入来分区图。在这种情况下，亲和力矩阵是图的邻近矩阵，SpectralFlowering初始化为 affinity='precomputed'

>>> from sklearn.cluster import SpectralClustering
>>> sc = SpectralClustering(3, affinity='precomputed', n_init=100,
...                         assign_labels='discretize')
>>> sc.fit_predict(adjacency_matrix)

2.3.6. 层次聚类#

分层集群是一个通用的集群算法家族，通过连续合并或分裂嵌套集群来构建嵌套集群。该集群层次结构被表示为树（或树图）。树根是收集所有样本的独特集群，叶子是只有一个样本的集群。看到 Wikipedia page 了解更多详细信息。

的 AgglomerativeClustering 对象使用自下而上的方法执行分层集群：每个观察从其自己的集群开始，然后集群被连续合并在一起。链接标准确定用于合并策略的指标：

Ward 最小化所有集群内的平方差和。这是一种方差最小化的方法，从这个意义上说，类似于k均值目标函数，但采用凝聚分层方法来处理。
Maximum 或 complete linkage 最小化成对集群的观察之间的最大距离。
Average linkage 最小化成对集群的所有观察之间的平均距离。
Single linkage 最小化成对集群的最近观察之间的距离。

AgglomerativeClustering 当与连接性矩阵联合使用时，它还可以扩展到大量样本，但当样本之间不添加连接性约束时，计算成本很高：它在每个步骤中都考虑所有可能的合并。

2.3.6.1. 不同的联动类型：病房联动、完全联动、平均联动和单一联动#

AgglomerativeClustering 支持沃德、单一、平均和完整联动策略。

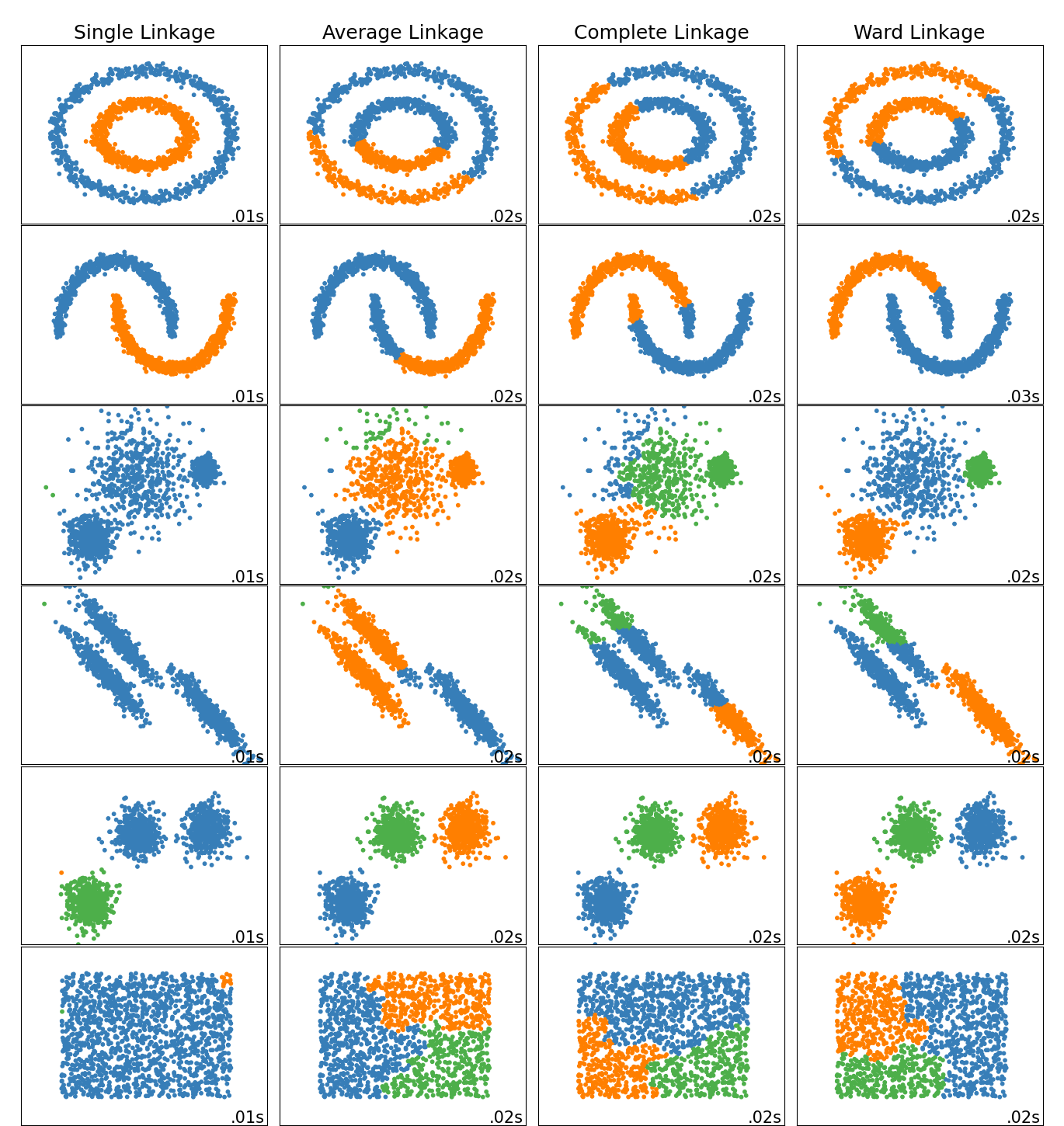
../_images/sphx_glr_plot_linkage_comparison_001.png

集聚集群具有“富得越富”的行为，导致集群规模不均匀。在这方面，单一联动是最糟糕的策略，沃德给出了最常规的尺寸。然而，亲和力（或集群中使用的距离）不能随Ward而变化，因此对于非欧几里得指标，平均联系是一个很好的替代方案。单一链接虽然对有噪数据不鲁棒，但可以非常有效地计算，因此有助于提供更大数据集的分层集群。单一链接也可以在非球状数据上表现良好。

示例

2D数字嵌入上的各种聚集性聚集：在一个真实的数据集中探索不同的联系策略。
- 在玩具数据集上比较不同的分层链接方法：探索玩具数据集中的不同链接策略。

2.3.6.2. 集群层次结构的可视化#

可以将代表集群分层合并的树可视化为树图。目视检查通常对于了解数据结构很有用，尽管在小样本量的情况下尤其如此。

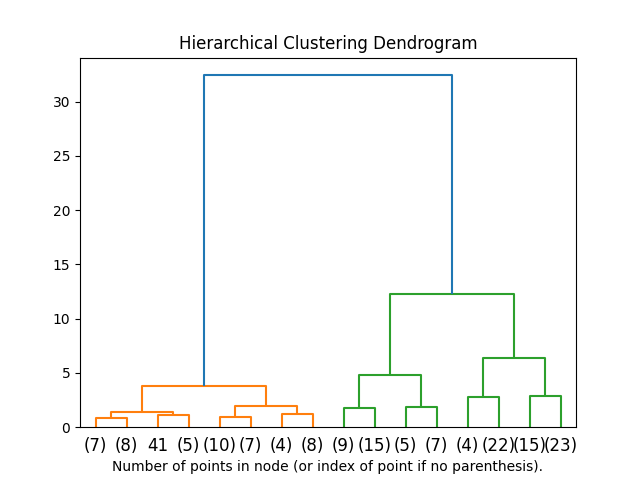
../_images/sphx_glr_plot_agglomerative_dendrogram_001.png

示例

图分层聚集树图

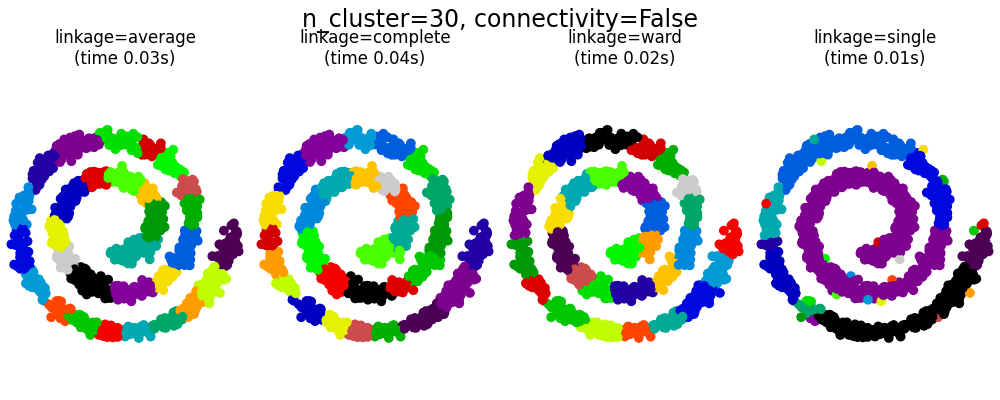
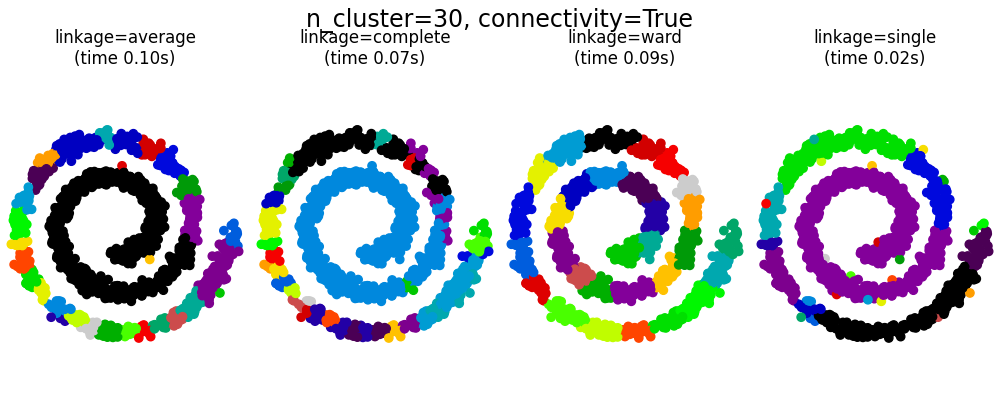
2.3.6.3. 添加连接约束#

的一个有趣的方面 AgglomerativeClustering 可以通过连通性矩阵将连通性约束添加到该算法中（只有相邻的聚类可以合并在一起），该连通性矩阵为每个样本定义了遵循给定数据结构的相邻样本。例如，在下面的swiss-roll示例中，连接性约束禁止合并在swiss roll上不相邻的点，从而避免形成跨该卷的重叠折叠延伸的聚类。

结构化

这些约束对于强加某种局部结构很有用，但它们也使算法更快，尤其是当样本数量较多时。

连接性约束是通过连接性矩阵施加的：一个Scipy稀疏矩阵，仅在行和列的交叉点处具有元素，该矩阵具有应该连接的数据集的索引。该矩阵可以根据先验信息构建：例如，您可能希望仅通过合并具有指向另一个的链接的页面来对网页进行集群。也可以从数据中学习，例如使用 sklearn.neighbors.kneighbors_graph 限制合并到最近的邻居，如在 this example ，或使用 sklearn.feature_extraction.image.grid_to_graph 仅允许合并图像上的邻近像素，如 coin example.

警告

Connectivity constraints with single, average and complete linkage

Connectivity constraints and single, complete or average linkage can enhance the 'rich getting richer' aspect of agglomerative clustering, particularly so if they are built with sklearn.neighbors.kneighbors_graph. In the limit of a small number of clusters, they tend to give a few macroscopically occupied clusters and almost empty ones. (see the discussion in 有结构和不有结构的集聚). Single linkage is the most brittle linkage option with regard to this issue.

../_images/sphx_glr_plot_agglomerative_clustering_001.png

../_images/sphx_glr_plot_agglomerative_clustering_002.png

../_images/sphx_glr_plot_agglomerative_clustering_003.png

../_images/sphx_glr_plot_agglomerative_clustering_004.png

示例

硬币图像上的结构化Ward分层集群演示：Ward集群将硬币图像分割为区域。
分层集群：结构化与非结构化病房：Swiss-roll上的Ward算法示例，结构化方法与非结构化方法的比较。
特征聚集与单变量选择：基于Ward分层集群的特征聚集降维示例。
有结构和不有结构的集聚

2.3.6.4. 改变指标#

Single, average and complete linkage can be used with a variety of distances (or affinities), in particular Euclidean distance (l2), Manhattan distance (or Cityblock, or l1), cosine distance, or any precomputed affinity matrix.

l1 距离通常对于稀疏特征或稀疏噪音有利：即许多特征都是零，就像使用罕见词出现的文本挖掘一样。
cosine 距离很有趣，因为它不受信号的全球缩放影响。

选择度量的准则是使用一个最大化不同类中样本之间的距离，并最小化每个类中的距离的度量。

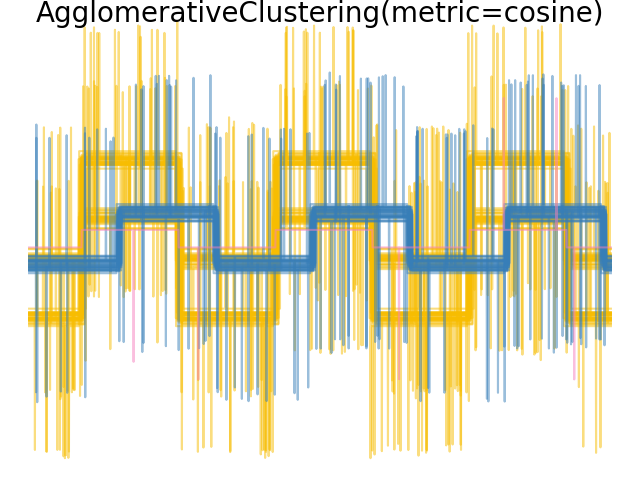
../_images/sphx_glr_plot_agglomerative_clustering_metrics_005.png

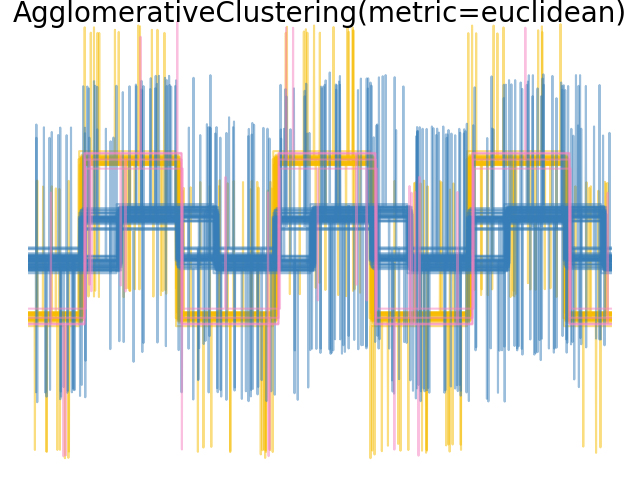
../_images/sphx_glr_plot_agglomerative_clustering_metrics_006.png

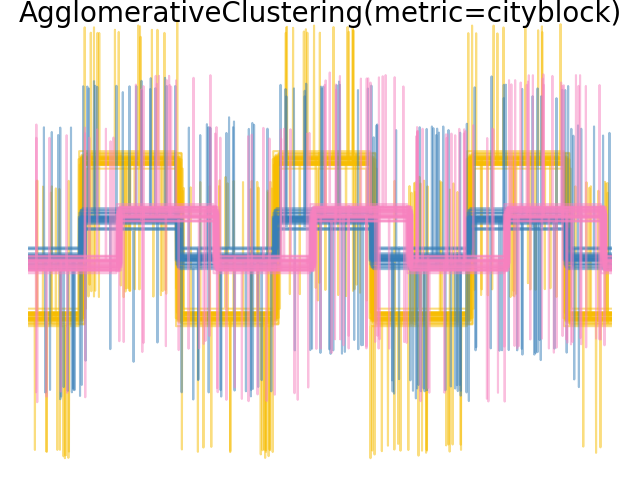
../_images/sphx_glr_plot_agglomerative_clustering_metrics_007.png

示例

具有不同指标的聚集性集群

2.3.6.5. 对分K均值#

的 BisectingKMeans 是的迭代变体 KMeans ，使用分裂的分层集群。不是一次创建所有重心，而是根据之前的集群逐步选择重心：一个集群被重复分成两个新集群，直到达到目标集群数量。

BisectingKMeans 效率高于 KMeans 当聚类的数量很大时，因为它只对每个二分处的数据的子集起作用， KMeans 始终适用于整个数据集。

虽然 BisectingKMeans 无法受益于 "k-means++" 通过设计初始化，它仍然会产生与之相当的结果 KMeans(init="k-means++") 就惯性而言，计算成本更低，并且可能会产生比 KMeans 具有随机初始化。

如果集群的数量与数据点的数量相比较小，则该变体对于聚集集群更有效。

该变体也不产生空簇。

选择要拆分的群集有两种策略：

bisecting_strategy="largest_cluster" 选择积分最多的集群
bisecting_strategy="biggest_inertia" 选择具有最大惯性的聚类（具有最大误差平方和的聚类）

在大多数情况下，通过最大数量的数据点进行拾取会产生与通过惯性进行拾取一样准确的结果，而且速度更快（特别是对于大量的数据点，计算误差可能会很高）。

根据最大数量的数据点进行挑选也可能会产生相似大小的集群， KMeans 已知会产生不同大小的集群。

从示例中可以看出二分K均值和常规K均值之间的差异二分K均值和常规K均值性能比较 .虽然常规的K-Means算法往往会创建不相关的集群，但来自Bitecting K-Means的集群排序良好，并创建了相当明显的层次结构。

2.3.7. DBSCAN#

的 DBSCAN 算法将集群视为被低密度区域分开的高密度区域。由于这种相当通用的观点，DBSCAN发现的集群可以是任何形状，而不是假设集群是凸面形状的k均值。DBSCAN的核心组件是 core samples ，它们是高密度区域的样本。因此，集群是一组核心样本，每个样本彼此靠近（通过某种距离测量），以及一组接近核心样本（但本身不是核心样本）的非核心样本。该算法有两个参数， min_samples 和 eps ，它正式定义了我们所说的意思 dense .更高 min_samples 或更低 eps 表示形成集群所需的更高密度。

更正式地，我们将核心样本定义为数据集中的样本，这样存在 min_samples 距离内的其他样本 eps ，其定义为 neighbors 核心样本的。这告诉我们，核心样本位于载体空间的密集区域。集群是一组核心样本，可以通过以下方式构建：以迭代方式获取核心样本，找到其所有邻居（即核心样本），找到所有 their 作为核心样本的邻居等等。集群还具有一组非核心样本，这些样本是集群中核心样本的邻居，但本身不是核心样本的样本。直觉上，这些样本位于星系团的边缘。

根据定义，任何核心样本都是集群的一部分。任何不是核心样本且至少是 eps 与任何核心样本的距离被算法视为离群值。

尽管参数 min_samples 主要控制算法对噪音的容忍程度（在有噪和大数据集上，可能需要增加此参数），参数 eps 是 crucial to choose appropriately 对于数据集和距离函数，通常不能保留为默认值。它控制点的本地邻近区域。当选择得太小时，大多数数据根本不会被聚集（并标记为 -1 代表“噪音”）。当选择得太大时，它会导致接近的集群合并到一个集群中，最终整个数据集作为单个集群返回。文献中已经讨论了选择该参数的一些启发式方法，例如基于最近邻距离图中的膝盖（如下参考文献中所讨论的）。

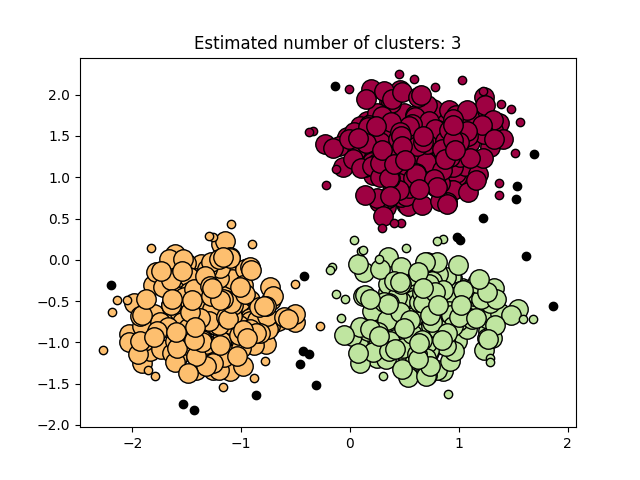
在下图中，颜色表示聚类成员，大圆圈表示算法找到的岩心样本。较小的圆圈是仍然是集群的一部分的非核心样本。此外，离群值由下面的黑点表示。

示例

DBSCAN集群算法演示

A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise 埃斯特，M.，H. P. Kriegel，J. Sander，and X. Xu，在第二届知识发现和数据挖掘国际会议论文集，波特兰，OR，AAAI出版社，pp. 226-231. 1996
DBSCAN revisited, revisited: why and how you should (still) use DBSCAN. 舒伯特，E.，桑德，J.，埃斯特，M.，克里格尔，H. P.，& Xu，X.（2017）。在ACN数据库系统交易（TODS）中，42（3），19。

2.3.8. HDBSCAN#

的 HDBSCAN 算法可以被视为 DBSCAN 和 OPTICS .具体来说， DBSCAN 假设聚集标准（即密度要求）是 globally homogeneous .换句话说， DBSCAN 可能很难成功捕获不同密度的集群。 HDBSCAN 通过构建集群问题的替代表示来证实这一假设并探索所有可能的密度尺度。

备注

该实现改编自HDSCAN的原始实现， scikit-learn-contrib/hdbscan 基于 [LJ2017].

示例

HDSCAN集群算法演示

2.3.8.1. 相互可达性图#

HDSCAN首先定义 \(d_c(x_p)\) ， core distance 样品 \(x_p\) ，作为到其距离 min_samples 最近的邻居，数着自己。例如如果 min_samples=5 和 \(x_*\) 是的第五近邻 \(x_p\) 那么核心距离是：

\[d_c（x_p）=d（x_p，x_*）。\]

Next it defines \(d_m(x_p, x_q)\), the mutual reachability distance of two points \(x_p, x_q\), as:

\[d_m（x_p，x_q）= \max\{d_c（x_p），d_c（x_q），d（x_p，x_q）\}\]

这两个概念使我们能够构建 mutual reachability graph \(G_{ms}\) 定义为固定的选择， min_samples 通过关联每个样本 \(x_p\) 具有图形的一个点，从而具有点之间的边 \(x_p, x_q\) 是相互可达性距离 \(d_m(x_p, x_q)\) 他们之间我们可以构建该图的子集，表示为 \(G_{ms,\varepsilon}\) ，方法是删除值大于 \(\varepsilon\) ：来自原始图表。核心距离小于的任何点 \(\varepsilon\) ：在这个阶段被标记为噪音。然后通过查找此修剪图的连接分量来对剩余点进行聚集。

备注

获取修剪图的连通分量 \(G_{ms,\varepsilon}\) 相当于运行DBSCAN * with min_samples and \(\varepsilon\). DBSCAN* 是中提到的DBSCAN的稍微修改版本 [CM2013].

2.3.8.2. 层次聚类#

HDBSCAN可以被视为一种算法，可以在所有值上执行DBSCAN* 集群 \(\varepsilon\) .如前所述，这相当于为所有值找到相互可达性图的连接分量 \(\varepsilon\) .为了有效地做到这一点，HDSCAN首先从全连接的相互可达性图中提取最小生成树（MST），然后贪婪地切割具有最高权重的边。HDSCAN算法的概要如下：

提取的MST \(G_{ms}\) .
通过为每个点添加“自边”来扩展MST，权重等于基础样本的核心距离。
初始化MST的单个集群和标签。
从MST中移除具有最大重量的边缘（同时移除系杆）。
将集群标签分配给包含现已删除边的端点的连接组件。如果组件至少没有一条边，则会被分配一个“空”标签，将其标记为噪音。
重复4-5，直到不再有连接的组件。

因此，HDBSCAN能够获得DBSCAN* 可实现的所有可能分区， min_samples 以分层的方式。事实上，这允许HDSCAN跨多个密度执行集群，因此不再需要 \(\varepsilon\) 作为超参数给出。相反，它完全依赖于选择 min_samples ，这往往是一个更强大的超参数。

HDBSCAN可以使用额外的超参数进行平滑 min_cluster_size 它指定在分层集群期间，少于 minimum_cluster_size 许多样本被认为是噪音。在实践中，可以设置 minimum_cluster_size = min_samples 以耦合参数并简化超参数空间。

引用

[CM2013]

Campello，R.J.G.B.，Moulavi，D.，Sander，J.（2013）.基于层次密度估计的密度聚类。在：Pei，J.，曾，VS，Cao，L.，元田，H.，徐，G. (eds)知识发现和数据挖掘的进展。PAKDD 2013。计算机科学讲座笔记（），第7819卷。施普林格、柏林、海德堡。 Density-Based Clustering Based on Hierarchical Density Estimates

[LJ2017]

L. McInnes and J. Healy, (2017). Accelerated Hierarchical Density Based Clustering. In: IEEE International Conference on Data Mining Workshops (ICDMW), 2017, pp. 33-42. Accelerated Hierarchical Density Based Clustering

2.3.9. OPTICS#

的 OPTICS 算法与 DBSCAN 算法，并且可以被认为是DBSCAN的概括，它放松了 eps 从一个值到一个值范围的要求。DBSCAN和OPTICS之间的关键区别在于OPTICS算法构建了一个 reachability 图，它为每个样本分配一个 reachability_ 距离，以及集群内的一个点 ordering_ 属性;这两个属性是在模型匹配时分配的，并用于确定集群成员资格。如果OPTICS以默认值运行 inf 设置 max_eps ，则可以在线性时间内重复执行DBSCAN风格的集群提取 eps 使用 cluster_optics_dbscan 法设置 max_eps 较低的值将导致更短的运行时间，并且可以被认为是从每个点寻找其他潜在可达点的最大邻居半径。

的 reachability OPTICS生成的距离允许在单个数据集中进行可变密度的集群提取。如上图所示，结合 reachability 距离和数据集 ordering_ 产生 reachability plot ，其中点密度在Y轴上表示，并且点的排序使得附近的点相邻。以单个值“切割”可达性图会产生类似DBSCAN的结果;“切割”上方的所有点都被归类为噪音，每次从左向右读取时出现中断都意味着一个新的集群。OPTICS的默认集群提取会查看图表中的陡坡以找到集群，用户可以使用参数定义什么算作陡坡 xi .对图本身进行分析还有其他可能性，例如通过可达性图树图生成数据的分层表示，并且可以通过 cluster_hierarchy_ 参数.上面的图已进行了颜色编码，以便平面空间中的聚类颜色与可达性图的线性分段聚类相匹配。请注意，蓝色和红色聚类在可达性图中相邻，可以分层表示为较大父聚类的子聚类。

示例

OPTICS分簇算法演示

2.3.10. BIRCH#

的 Birch 为给定数据构建一棵称为集群特征树（CFT）的树。数据本质上被有损压缩到一组集群特征节点（CF节点）。CF节点具有许多称为聚集特征子集群（CF子集群）的子集群，并且位于非终端CF节点中的这些CF子集群可以将CF节点作为子节点。

CF子集群保存集群所需的信息，从而避免需要将整个输入数据保存在内存中。此信息包括：

子集群中的样本数。
线性和-一个n维载体，保存所有样本的和
平方和-所有样本的L2模平方的和。
Centroids -为了避免重新计算线性总和/ n_samples。
重心的平方规范。

The BIRCH algorithm has two parameters, the threshold and the branching factor. The branching factor limits the number of subclusters in a node and the threshold limits the distance between the entering sample and the existing subclusters.

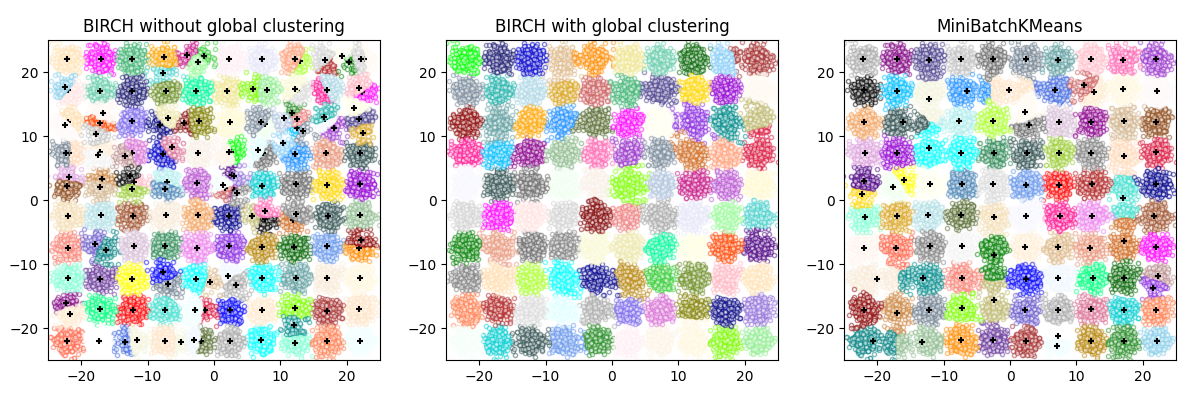
该算法可以被视为一个实例或数据简化方法，因为它将输入数据简化为直接从CFT的叶子中获得的一组子聚类。这种减少的数据可以通过将其馈送到全局聚类器中来进一步处理。该全局聚类器可以通过以下方式设置： n_clusters .如果 n_clusters 设置为无，则直接读取叶子的子集群，否则全局集群步骤将这些子集群标记为全局集群（标签），并将样本映射到最近的子集群的全局标签。

2.3.11. 集群绩效评估#

评估集群算法的性能并不像计算错误数量或监督分类算法的精确度和召回率那么简单。特别是，任何评估指标都不应考虑集群标签的绝对值，而是如果这种集群定义了类似于某些基本事实类集的数据分离或满足某些假设，使得属于同一类的成员比不同类的成员更相似根据一些相似性指标。

2.3.11.1. 兰德指数#

鉴于对基本真相课堂作业的了解 labels_true 以及我们对相同样本的聚集算法分配 labels_pred ， (adjusted or unadjusted) Rand index 是一个函数， similarity 在两个赋值中，忽略排列：

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.rand_score(labels_true, labels_pred)
0.66

兰德指数并不能确保随机标签获得接近0.0的值。调整后的兰德指数 corrects for chance 并将给出这样的基线。

>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

与所有集群指标一样，可以在预测标签中置换0和1，将2重命名为3，并获得相同的分数：：

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.rand_score(labels_true, labels_pred)
0.66
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

此外，两者 rand_score 和 adjusted_rand_score 是 symmetric ：交换论点不会改变分数。因此，它们可以用作 consensus measures

>>> metrics.rand_score(labels_pred, labels_true)
0.66
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24

完美标签评分为1.0：：

>>> labels_pred = labels_true[:]
>>> metrics.rand_score(labels_true, labels_pred)
1.0
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0

一致性较差的标签（例如独立标签）的得分较低，并且对于调整后的兰德指数，得分将为负或接近零。然而，对于未经调整的兰德指数，分数虽然较低，但不一定接近零：：

>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1]
>>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6]
>>> metrics.rand_score(labels_true, labels_pred)
0.39
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.072

优点：

Interpretability ：未调整的兰德指数与两者标签相同的样本对的数量成正比 labels_pred 和 labels_true ，或者两者都不同。
Random (uniform) label assignments have an adjusted Rand index score close to 0.0 对于任何价值 n_clusters 和 n_samples （例如，对于未经调整的兰德指数或V-度量，情况并非如此）。
Bounded range ：较低的值表示不同的标签，类似的集群具有较高的（调整或未调整）兰德指数，1.0是完美匹配分数。得分范围为 [0, 1] 对于未经调整的兰德指数和 [-0.5, 1] 对于调整后的兰德指数。
No assumption is made on the cluster structure ：（调整或未调整）兰德指数可用于比较各种集群算法，并可用于比较假设各向同性斑点形状的k均值等集群算法与可以找到具有“折叠”形状的集群的谱集群算法的结果。

示例

集群绩效评估中的机会调整分析数据集大小对随机分配的聚类度量值的影响。

2.3.11.2. 基于互信息的分数#

鉴于对基本真相课堂作业的了解 labels_true 以及我们对相同样本的聚集算法分配 labels_pred ， Mutual Information 是一个函数， agreement 两个赋值，忽略排列。该度量有两种不同的标准化版本， Normalized Mutual Information (NMI) 和 Adjusted Mutual Information (AMI) . NMI经常在文献中使用，而AMI是最近提出的， normalized against chance

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

可以在预测标签中排列0和1，将2重命名为3并获得相同的分数：：

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

所有的， mutual_info_score , adjusted_mutual_info_score 和 normalized_mutual_info_score 是对称的：交换参数不会改变分数。因此它们可以用作 consensus measure

>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504

完美标签评分为1.0：：

>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0

>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0

这对于 mutual_info_score ，因此更难判断：：

>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69

不良（例如独立标签）的评分为非阳性：：

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526

示例

集群绩效评估中的机会调整分析数据集大小对随机分配的聚类度量值的影响。此示例还包括调整后兰德指数。

数学公式#

假设两个标签分配（相同的N个对象）， \(U\) 和 \(V\) .它们的熵是分区集的不确定性量，定义如下：

\[H(U) = - \sum_{i=1}^{|U|}P(i)\log(P(i))\]

哪里 \(P(i) = |U_i| / N\) 是从 \(U\) 落入类 \(U_i\) .同样对于 \(V\) :

\[H(V) = - \sum_{j=1}^{|V|}P'(j)\log(P'(j))\]

与 \(P'(j) = |V_j| / N\) .之间的互信息（MI） \(U\) 和 \(V\) 计算公式为：

\[\text{MI}(U, V) = \sum_{i=1}^{|U|}\sum_{j=1}^{|V|}P(i, j)\log\left(\frac{P(i,j)}{P(i)P'(j)}\right)\]

哪里 \(P(i, j) = |U_i \cap V_j| / N\) 是随机选择的对象属于这两类的概率 \(U_i\) 和 \(V_j\) .

它也可以用集合基数公式表示：

\[\text{MI}(U, V) = \sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \frac{|U_i \cap V_j|}{N}\log\left(\frac{N|U_i \cap V_j|}{|U_i||V_j|}\right)\]

归一化互信息被定义为：

\[\text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))}\]

互信息以及规范化变体的这个值不会根据偶然性进行调整，并且往往会随着不同标签（集群）数量的增加而增加，无论标签分配之间“互信息”的实际量如何。

The expected value for the mutual information can be calculated using the following equation [VEB2009]. In this equation, \(a_i = |U_i|\) (the number of elements in \(U_i\)) and \(b_j = |V_j|\) (the number of elements in \(V_j\)).

\[E[\text{MI}(U,V)]=\sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \sum_{n_{ij}=(a_i+b_j-N)^+ }^{\min(a_i, b_j)} \frac{n_{ij}}{N}\log \left( \frac{ N.n_{ij}}{a_i b_j}\right) \frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})! (N-a_i-b_j+n_{ij})!}\]

使用预期值，然后可以使用与调整后的兰德指数类似的形式来计算调整后的互信息：

\[\text{AMI} = \frac{\text{MI} - E[\text{MI}]}{\text{mean}(H(U), H(V)) - E[\text{MI}]}\]

对于规范化互信息和调整后互信息，规范化值通常为一些 generalized 每个聚类的熵的平均值。存在着各种各样的一般化手段，但没有明确的规则来规定哪一种手段优于另一种手段。这个决定主要是一个领域一个领域的基础上，例如，在社区检测，算术平均值是最常见的。每种标准化方法都提供了“定性相似的行为” [YAT2016]. 在我们的实现中，这由 average_method 参数.

Vinh等人（2010）通过平均法命名了NMI和AMI的变体 [VEB2010]. 它们的“平方”和“总和”平均值是几何和算术平均值;我们使用这些更广泛的常用名称。

引用

Strehl、Alexander和Joydeep Ghosh（2002）。“集群集成-用于组合多个分区的知识重用框架”。机器学习研究杂志3：583-617。 doi:10.1162/153244303321897735 .
Wikipedia entry for the (normalized) Mutual Information <https://en.wikipedia.org/wiki/Mutual_Information> _
Wikipedia entry for the Adjusted Mutual Information <https://en.wikipedia.org/wiki/Adjusted_Mutual_Information> _

[VEB2009]

Vinh、Epps和Bailey，（2009）。“集群比较的信息论测量”。第26届国际机器学习年度会议录- ICML ' 09。 doi:10.1145/1553374.1553511 . ISBN 9781605585161。

[VEB2010]

Vinh、Epps和Bailey，（2010）。“交叉比较的信息论测量：变体、性质、规范化和机会修正”。JMLR <https://jmlr.csail.mit.edu/papers/volume11/vinh10a/vinh10a.pdf>

[YAT2016]

Yang、Algesheimer和Tessone，（2016）。“人工网络上社区检测算法的比较分析”。科学报告6：30750。 doi:10.1038/srep30750 .

2.3.11.3. 齐性、完整性和V-测量#

考虑到样本的基本真值类分配的知识，可以使用条件熵分析定义一些直观的指标。

特别是Rosenberg和Hirschberg（2007）为任何集群分配定义了以下两个理想目标：

homogeneity ：每个集群仅包含单个类的成员。
completeness ：给定类别的所有成员都被分配到同一集群。

我们可以把这些概念作为分数 homogeneity_score 和 completeness_score .两者的下限为0.0，上限为1.0（越高越好）：：

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66

>>> metrics.completeness_score(labels_true, labels_pred)
0.42

它们的和声平均值称为 V-measure 计算方法是 v_measure_score

>>> metrics.v_measure_score(labels_true, labels_pred)
0.516

该函数的公式如下：

\[v = \frac{(1 + \beta) \times \text{homogeneity} \times \text{completeness}}{(\beta \times \text{homogeneity} + \text{completeness})}\]

beta 默认值为1.0，但对于Beta版使用小于1的值：：

>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.547

更多的权重将归因于同质性，并使用大于1的值：：

>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48

将更重视完整性。

V-测量实际上相当于上面讨论的互信息（NMI），聚合函数是算术平均值 [B2011].

齐性、完整性和V-测量可以使用以下方法同时计算 homogeneity_completeness_v_measure 如下：：

>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.67, 0.42, 0.52)

下面的集群分配稍微好一点，因为它是同质的但不完整的：：

>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68, 0.81)

备注

v_measure_score 是 symmetric ：它可以用于评估 agreement 同一数据集上的两个独立分配。

并非如此 completeness_score 和 homogeneity_score ：两者都受到关系的约束：：

homogeneity_score(a, b) == completeness_score(b, a)

示例

集群绩效评估中的机会调整分析数据集大小对随机分配的聚类度量值的影响。

引用

V-Measure: A conditional entropy-based external cluster evaluation measure 安德鲁·罗森伯格和朱莉娅·赫希伯格，2007年

[B2011]

Identification and Characterization of Events in Social Media <http://www.cs.columbia.edu/~hila/hila-thesis-distributed.pdf> _，Hila Becker，博士论文。

2.3.11.4. 福克斯-马洛斯得分#

最初的Fowlkes-Malows指数（LDI）旨在衡量两个集群结果之间的相似性，这本质上是一种无监督比较。Fowlkes-Malows指数的监督适应（如在中实现的 sklearn.metrics.fowlkes_mallows_score ）可以在已知样本的基础真值类分配时使用。FMI定义为成对查准率和查全率的几何平均值：

\[\text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}}\]

在上面的公式中：

TP ( True Positive ）：在真实标签和预测标签中聚集在一起的点对的数量。
FP ( False Positive ）：在预测标签中聚集在一起但不在真实标签中聚集在一起的点对的数量。
FN ( False Negative ）：在真实标签中聚集在一起但不在预测标签中聚集在一起的点对的数量。

分数范围为0到1。高值表示两个聚类之间具有良好的相似性。

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

可以在预测标签中排列0和1，将2重命名为3并获得相同的分数：：

>>> labels_pred = [1, 1, 0, 0, 3, 3]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

完美标签评分为1.0：：

>>> labels_pred = labels_true[:]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
1.0

不良（例如独立标签）得分为零：：

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0

2.3.11.5. Silhouette Coefficient#

如果基础事实标签未知，则必须使用模型本身执行评估。剪影系数 (sklearn.metrics.silhouette_score ）是此类评估的一个例子，其中较高的轮廓系数分数与具有更好定义的集群的模型相关。轮廓系数是为每个样本定义的，由两个分数组成：

a ：样本与同一类中所有其他点之间的平均距离。
b ：样本与中所有其他点之间的平均距离 next nearest cluster .

剪影系数 s 对于单个样本，则给出为：

\[s = \fRAC{b - a}{max（a，b）}\]

一组样本的轮廓系数以每个样本的轮廓系数的平均值给出。

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

在正常使用中，轮廓系数应用于集群分析的结果。

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55

示例

在KMeans聚类中使用轮廓分析选择聚类数在这个例子中，轮廓分析用于选择n_clusters的最佳值。

2.3.11.6. 卡林斯基-哈拉巴斯指数#

如果地面真相标签未知，则使用Calinski-Harabasz指数 (sklearn.metrics.calinski_harabasz_score ）--也称为方差比标准--可用于评估模型，其中较高的Calinski-Harabasz分数与具有更好定义的集群的模型相关。

指数是所有集群的集群间分散度和集群内分散度之和的比率（其中分散度定义为距离平方的和）：

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

在正常使用中，Calinski-Harabasz指数应用于集群分析的结果：

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.59

2.3.11.7. 戴维斯-布尔丁指数#

如果不知道基本真相标签，Davies-Bouldin指数 (sklearn.metrics.davies_bouldin_score ）可用于评估模型，其中较低的Davies-Bouldin指数与集群之间分离更好的模型相关。

该指数表示集群之间的平均“相似性”，其中相似性是将集群之间的距离与集群本身的大小进行比较的测量。

零是可能的最低分数。接近零的值表示更好的分区。

在正常使用中，Davies-Bouldin指数应用于如下集群分析的结果：

>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> from sklearn.cluster import KMeans
>>> from sklearn.metrics import davies_bouldin_score
>>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans.labels_
>>> davies_bouldin_score(X, labels)
0.666

2.3.11.8. 应急矩阵#

权宜矩阵 (sklearn.metrics.cluster.contingency_matrix ）报告每个真/预测聚类对的交集基数。列联矩阵为所有聚类度量提供了足够的统计数据，其中样本是独立和相同分布的，并且不需要考虑一些未被聚类的实例。

这是一个例子：：

>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
       [0, 1, 2]])

输出数组的第一行指示有三个样本的真实集群是“a”。其中，两个位于预测的集群0中，一个位于1中，没有一个位于2中。第二行指示有三个样本的真实集群是“b”。其中，没有一个在预测的集群0中，一个在1中，两个在2中。

A confusion matrix 分类是一个方形列联矩阵，其中行和列的顺序对应于类列表。

2.3.11.9. 配对混淆矩阵#

配对混淆矩阵 (sklearn.metrics.cluster.pair_confusion_matrix ）是2x 2相似性矩阵

\[\begin{split}C = \left[\begin{matrix} C_{00} & C_{01} \\ C_{10} & C_{11} \end{matrix}\right]\end{split}\]

通过考虑所有样本对并计数在真实和预测的集群下分配到相同或不同集群的对来计算两个集群之间。

它有以下条目：

\(C_{00}\) ：具有两个聚类的对的数量，其中样本没有聚类在一起

\(C_{10}\) ：具有将样本聚集在一起但另一个聚集不具有样本聚集在一起的真实标签聚集对的数量

\(C_{01}\) ：具有真实标签集群的对数量，该真实标签集群没有将样本集群在一起，但另一个集群具有将样本集群在一起

\(C_{11}\) ：两个集群将样本聚集在一起的对数

将聚集在一起的一对样本视为正对，那么在二进制分类中，真阴性的计数是 \(C_{00}\) ，假阴性是 \(C_{10}\) ，真正的积极因素是 \(C_{11}\) 假阳性是 \(C_{01}\) .

完美匹配的标签在对角线上具有所有非零条目，无论实际标签值如何：：

>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
       [0, 4]])

>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
       [0, 4]])

将所有类成员分配到相同集群的标签是完整的，但可能不总是纯的，因此会受到惩罚，并且有一些非对角线非零条目：：

>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
       [0, 2]])

矩阵不对称：：

>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
       [2, 2]])

如果类成员完全分散在不同的集群中，则分配是完全不完整的，因此矩阵的对角线条目全部为零：：

>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0,  0],
       [12,  0]])