Ctrl+K

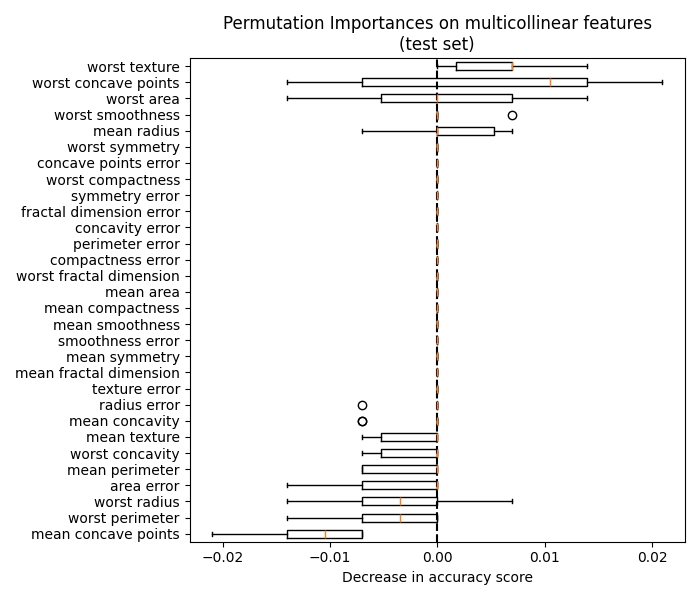
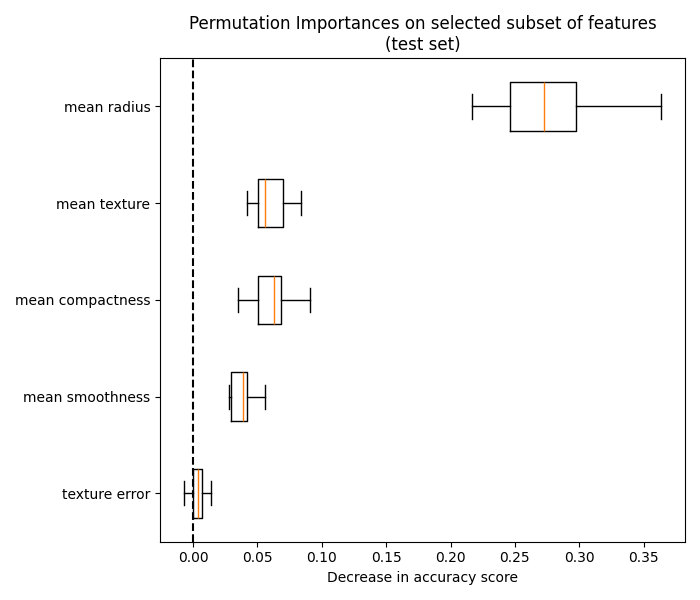
5.2. 排列特征重要性#

排列特征重要性是一种模型检查技术，衡量每个特征对 fitted 模型在给定表格数据集上的统计性能。该技术对于非线性或不透明特别有用 estimators ，并涉及随机洗牌单个特征的值并观察由此产生的模型分数退化 [1]. 通过打破特征和目标之间的关系，我们可以确定模型对这种特定特征的依赖程度。

在下图中，我们观察了置换特征对特征与目标之间相关性的影响，从而对模型统计性能的影响。

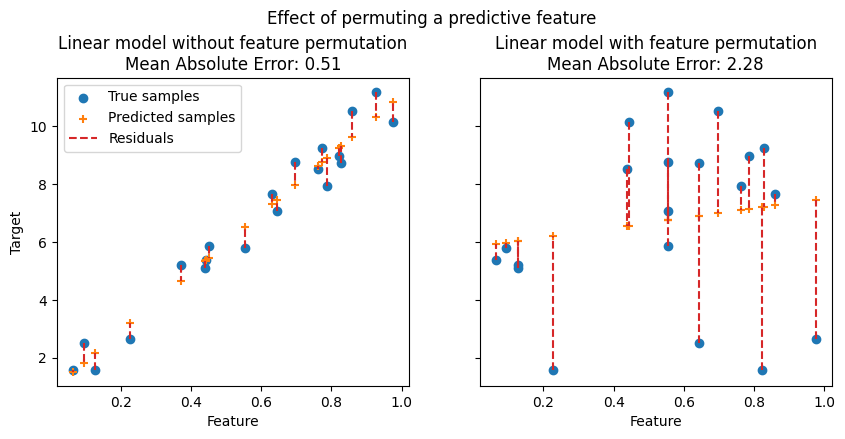
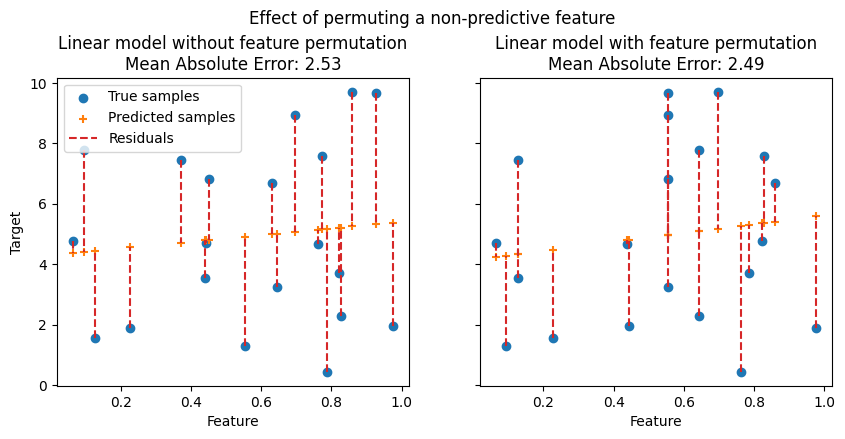
../_images/permuted_predictive_feature.png ../_images/permuted_non_predictive_feature.png

在上图中，我们观察到排列预测特征会破坏特征与目标之间的相关性，从而模型的统计性能下降。在底部的图中，我们观察到置换非预测性特征不会显着降低模型的统计性能。

排列特征重要性的一个关键优点是它是模型不可知的，即它可以应用于任何适合的估计器。此外，可以通过特征的不同排列多次计算它，进一步提供特定训练模型的估计特征重要性方差的测量。

下图显示了一个的排列特征重要性 RandomForestClassifier 在泰坦尼克号数据集的增强版本上训练，该数据集包含 random_cat 和 random_num 特征，即与目标变量不以任何方式相关的类别和数字特征：

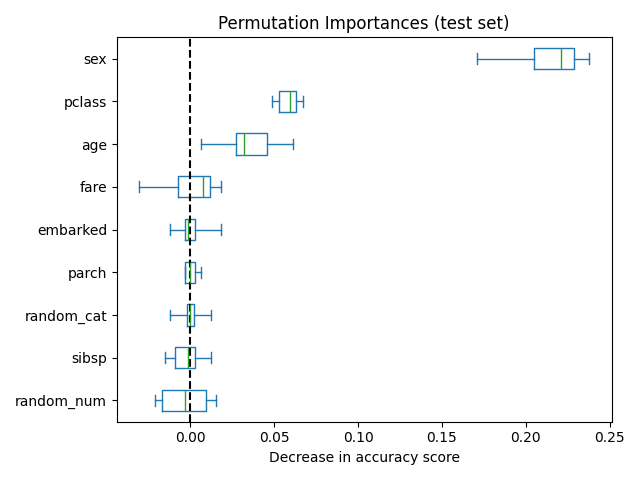
../_images/sphx_glr_plot_permutation_importance_002.png

警告

被认为的功能 low importance for a bad model (low交叉验证分数）可能是 very important for a good model .因此，在计算重要性之前，使用保留集（或更好地使用交叉验证）评估模型的预测能力始终很重要。排列重要性并不反映特征本身的内在预测价值， how important this feature is for a particular model .

的 permutation_importance 函数计算的特征重要性 estimators 对于给定的数据集。的 n_repeats 参数设置特征随机混洗的次数，并返回特征重要性的样本。

让我们考虑以下经过训练的回归模型：：

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import Ridge
>>> diabetes = load_diabetes()
>>> X_train, X_val, y_train, y_val = train_test_split(
...     diabetes.data, diabetes.target, random_state=0)
...
>>> model = Ridge(alpha=1e-2).fit(X_train, y_train)
>>> model.score(X_val, y_val)
0.356...

通过 \(R^2\) 分数，明显大于机会水平。这使得使用 permutation_importance 用于探测哪些特征最具预测性的功能：：

>>> from sklearn.inspection import permutation_importance
>>> r = permutation_importance(model, X_val, y_val,
...                            n_repeats=30,
...                            random_state=0)
...
>>> for i in r.importances_mean.argsort()[::-1]:
...     if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
...         print(f"{diabetes.feature_names[i]:<8}"
...               f"{r.importances_mean[i]:.3f}"
...               f" +/- {r.importances_std[i]:.3f}")
...
s5      0.204 +/- 0.050
bmi     0.176 +/- 0.048
bp      0.088 +/- 0.033
sex     0.056 +/- 0.023

请注意，顶级特征的重要性值代表参考分数0.356的很大一部分。

排列重要性可以在训练集或已发布的测试或验证集上计算。使用保留集可以突出显示哪些特征对所检查模型的概括能力贡献最大。对训练集中很重要但对保留集中不重要的特征可能会导致模型过度适应。

排列特征的重要性取决于用 scoring 论点此参数接受多个评分器，这比顺序调用计算效率更高 permutation_importance 多次使用不同的评分器，因为它重复使用模型预测。

使用多个评分器的置换特征重要性示例#

在下面的示例中，我们使用了一系列指标，但可能有更多的输入格式，如中所述 使用多指标评估 .

>>> scoring = ['r2', 'neg_mean_absolute_percentage_error', 'neg_mean_squared_error']
>>> r_multi = permutation_importance(
...     model, X_val, y_val, n_repeats=30, random_state=0, scoring=scoring)
...
>>> for metric in r_multi:
...     print(f"{metric}")
...     r = r_multi[metric]
...     for i in r.importances_mean.argsort()[::-1]:
...         if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
...             print(f"    {diabetes.feature_names[i]:<8}"
...                   f"{r.importances_mean[i]:.3f}"
...                   f" +/- {r.importances_std[i]:.3f}")
...
r2
    s5      0.204 +/- 0.050
    bmi     0.176 +/- 0.048
    bp      0.088 +/- 0.033
    sex     0.056 +/- 0.023
neg_mean_absolute_percentage_error
    s5      0.081 +/- 0.020
    bmi     0.064 +/- 0.015
    bp      0.029 +/- 0.010
neg_mean_squared_error
    s5      1013.866 +/- 246.445
    bmi     872.726 +/- 240.298
    bp      438.663 +/- 163.022
    sex     277.376 +/- 115.123

即使重要性值的规模非常不同，对于不同的指标，功能的排名也大致相同。然而，这并不能保证，不同的指标可能会导致明显不同的特征重要性，特别是对于针对不平衡分类问题训练的模型，对于 the choice of the classification metric can be critical .

5.2.1. 排列重要性算法概述#

  • 输入：适合的预测模型 \(m\) 、表格数据集（训练或验证） \(D\) .

  • 计算参考分数 \(s\) 模型 \(m\) 数据 \(D\) (for例如分类器的准确性或 \(R^2\) 对于回归者）。

  • 针对每个特征 \(j\) （列 \(D\) ):

    • 对于每次重复 \(k\) 在 \({1, ..., K}\) :

      • 随机洗牌列 \(j\) 数据集 \(D\) 生成名为 \(\tilde{D}_{k,j}\) .

      • 计算得分 \(s_{k,j}\) 模型 \(m\) 关于损坏的数据 \(\tilde{D}_{k,j}\) .

    • 计算重要性 \(i_j\) 用于特征 \(f_j\) 定义为：

      \[i_j = s - \frac{1}{K} \sum_{k=1}^{K} s_{k，j}\]

5.2.2. 与树木中基于杂质的重要性的关系#

基于树的模型提供了另一种测量方法 feature importances based on the mean decrease in impurity （计量吸入器）。通过决策树的分裂标准（基尼系数、对数损失或均方误差）量化杂质。然而，当模型过度适应时，这种方法可以对不可见数据进行预测的特征给予高度重要性。另一方面，基于排列的特征重要性可以避免这个问题，因为它可以根据不可见的数据计算。

此外，基于杂质的特征对树木的重要性是 strongly biased 和 favor high cardinality features （通常是数字特征）而不是低基数特征，例如具有少量可能类别的二元特征或类别变量。

基于置换的特征重要性不表现出这样的偏差。此外，置换特征重要性可以用模型预测的任何性能度量来计算，并且可以用于分析任何模型类（不仅仅是基于树的模型）。

以下示例强调了基于杂质的特征重要性与基于排列的特征重要性相比的局限性： 排列重要性与随机森林特征重要性（Millennium） .

5.2.3. 强相关特征上的误导性价值观#

当两个特征相关并且其中一个特征被排列时，模型仍然可以通过其相关特征访问后者。这导致这两个功能的报告重要性值较低，尽管它们可能 actually 很重要。

下图显示了一个的排列特征重要性 RandomForestClassifier 使用 威斯康星州乳腺癌（诊断）数据集 ，其中包含强相关的特征。天真的解释会表明所有功能都不重要：

../_images/sphx_glr_plot_permutation_importance_multicollinear_002.png

处理该问题的一种方法是对相关的特征进行集群，并且每个集群只保留一个特征。

../_images/sphx_glr_plot_permutation_importance_multicollinear_004.png

有关此类策略的更多详细信息，请参阅示例 具有多重共线或相关特征的排列重要性 .

示例

引用

On this page