2.5. 将信号分解为分量（矩阵分解问题）

2.5.1. 主成分分析（PCA）

2.5.1.1. 精确的PCA和概率解释

PCA用于将多变量数据集分解为一组连续的正交分量，这些正交分量解释了方差的最大量。在scikit-learn中， PCA 被实现为 transformer 学习的对象 \(n\) 其组件 fit 方法，并且可以用于新数据以将其投影到这些组件上。

在应用奇异值分解之前，PCA以每个特征的输入数据为中心，但不会缩放每个特征的输入数据。可选参数 whiten=True 使得可以将数据投影到奇异空间，同时将每个分量缩放到单位方差。如果下游模型对信号的各向同性做出强烈假设，这通常是有用的：例如，具有RBS核和K均值集群算法的支持载体机就是这种情况。

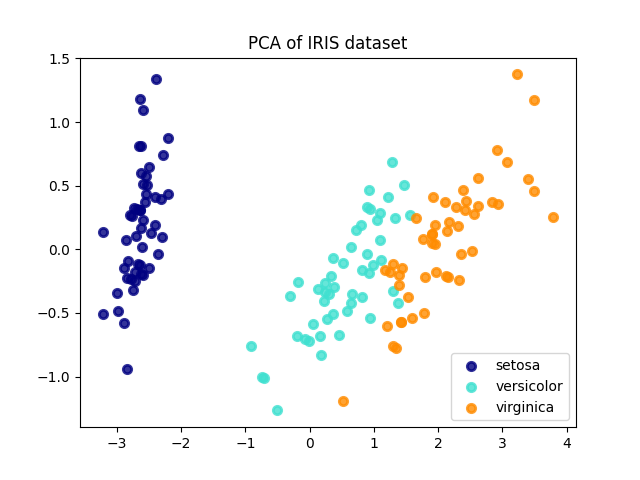
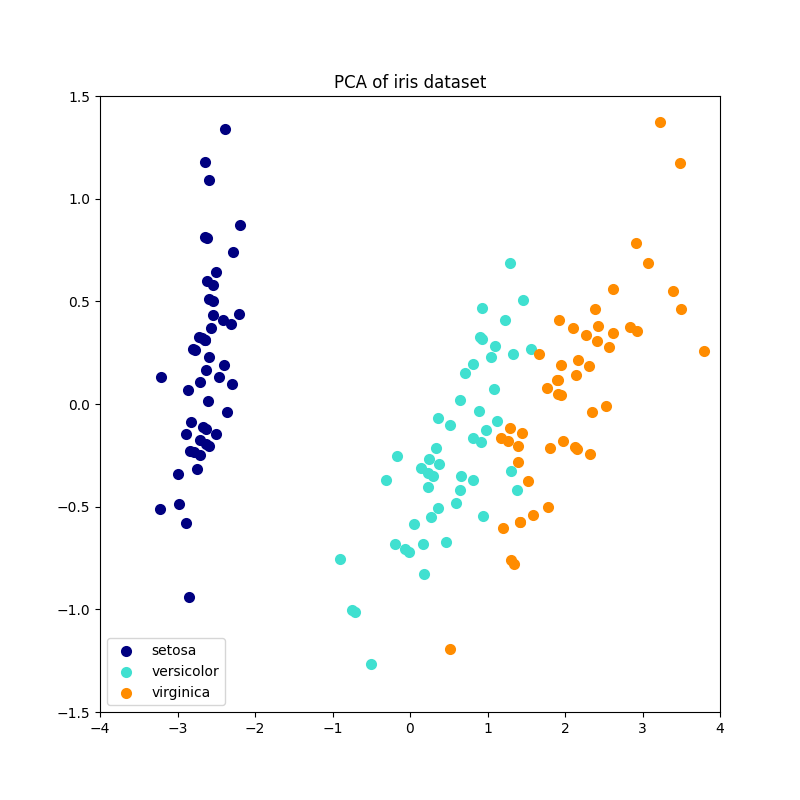
以下是虹膜数据集的示例，该数据集由4个特征组成，投影在解释大多数方差的2个维度上：

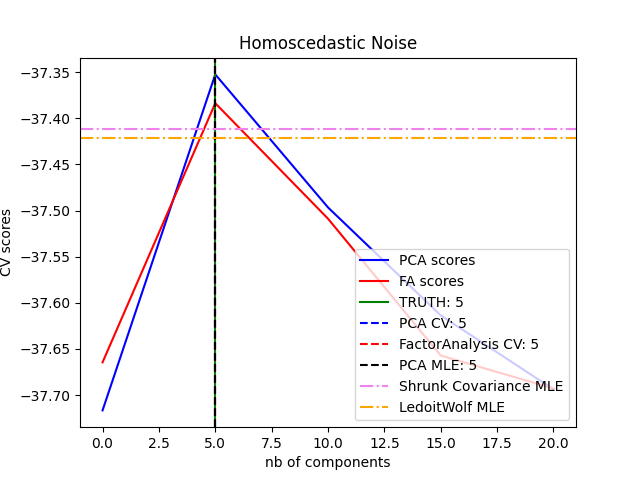
的 PCA 对象还提供了PCA的概率解释，可以根据其解释的方差量给出数据的可能性。因此，它实现了 score 可用于交叉验证的方法：

示例

• Iris数据集的主成分分析（PCA）

• Iris数据集LDA和PCA 2D投影的比较

• 使用概率PCA和因子分析（FA）进行模型选择

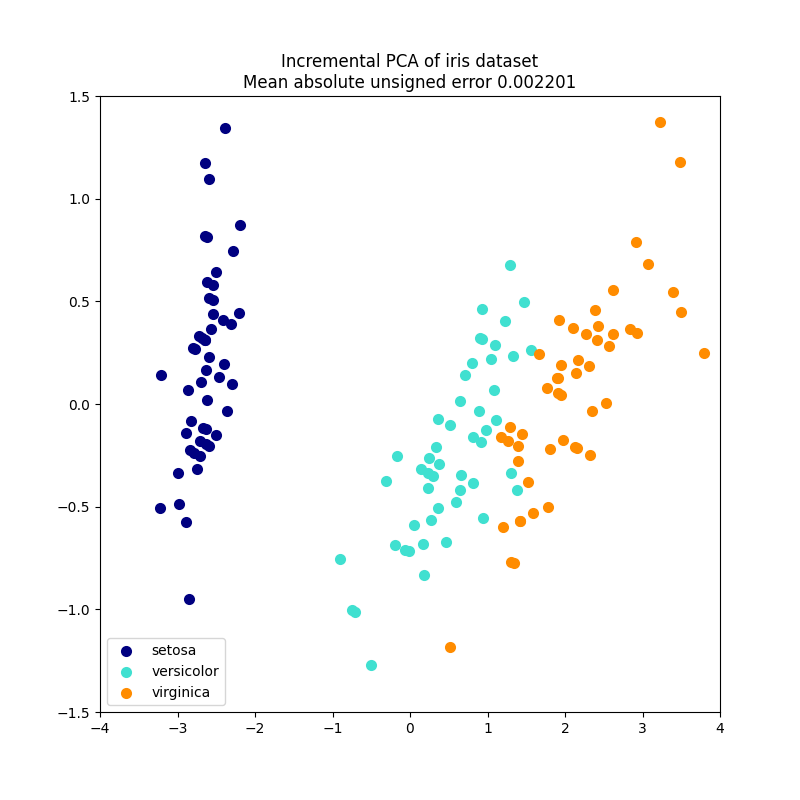
2.5.1.2. 增量PCA

的 PCA 对象非常有用，但对于大型数据集有一定的局限性。最大的限制是 PCA 仅支持批处理，这意味着所有要处理的数据必须容纳在主存储器中。的 IncrementalPCA 对象使用不同形式的处理，并允许几乎完全匹配的结果的部分计算 PCA 同时以小批方式处理数据。 IncrementalPCA 可以通过以下方式实施核心外主成分分析：

• 使用其 partial_fit 对从本地硬盘驱动器或网络数据库顺序提取的数据块的方法。

• 使用在内存映射文件上调用其fit方法 numpy.memmap .

IncrementalPCA only stores estimates of component and noise variances, in order to update explained_variance_ratio_ incrementally. This is why memory usage depends on the number of samples per batch, rather than the number of samples to be processed in the dataset.

如在 PCA , IncrementalPCA 在应用奇异值分解之前，中心但不会缩放每个要素的输入数据。

示例

• 增量PCA

2.5.1.3. 使用随机瓣膜分解的PCA

通过删除与较低奇异值相关的分量的奇异载体，将数据投影到保留大部分方差的较低维空间通常很有趣。

例如，如果我们使用64x64像素的灰度图像进行人脸识别，则数据的维数为4096，并且在如此宽的数据上训练RBF支持向量机是缓慢的。此外，我们知道数据的内在维度远低于4096，因为所有人脸的照片看起来都有点相似。样本位于维数低得多的流形上（例如大约200）。PCA算法可用于线性变换数据，同时降低维度并同时保留大部分解释的方差。

类 PCA 与可选参数一起使用 svd_solver='randomized' 在这种情况下非常有用：由于我们将丢弃大多数奇异向量，因此将计算限制为奇异向量的近似估计会更有效，我们将保持实际执行变换。

例如，以下显示了Olivetti数据集的16个样本肖像（以0.0为中心）。右手边是重塑为肖像的前16个奇异载体。由于我们只需要具有大小的数据集的前16个奇异载体 \(n_{samples} = 400\) 和 \(n_{features} = 64 \times 64 = 4096\) ，计算时间小于1秒：

orig_IMG pca_IMG

If we note \(n_{\max} = \max(n_{\mathrm{samples}}, n_{\mathrm{features}})\) and \(n_{\min} = \min(n_{\mathrm{samples}}, n_{\mathrm{features}})\), the time complexity of the randomized PCA is \(O(n_{\max}^2 \cdot n_{\mathrm{components}})\) instead of \(O(n_{\max}^2 \cdot n_{\min})\) for the exact method implemented in PCA.

The memory footprint of randomized PCA is also proportional to \(2 \cdot n_{\max} \cdot n_{\mathrm{components}}\) instead of \(n_{\max} \cdot n_{\min}\) for the exact method.

注：实施 inverse_transform 在 PCA 与 svd_solver='randomized' 不是的精确逆变换 transform 即使 whiten=False （默认）。

示例

• 使用特征脸和SVM的人脸识别示例

• Faces数据集分解

引用

• 算法4.3中 "Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions" Halko等人，2009

• "An implementation of a randomized algorithm for principal component analysis" A. Szlam等人2014

2.5.1.4. 稀疏主成分分析（SparsePCA和MiniBatchSparsePCA）

SparsePCA 是PCA的一种变体，其目标是提取最佳重建数据的稀疏分量集。

Mini-batch sparse PCA (MiniBatchSparsePCA) is a variant of SparsePCA that is faster but less accurate. The increased speed is reached by iterating over small chunks of the set of features, for a given number of iterations.

主成分分析 (PCA ）的缺点是，通过该方法提取的成分具有排他性密集的表达，即当它们表示为原始变量的线性组合时，它们具有非零系数。这可能会使解释变得困难。在许多情况下，真正的底层组件可以更自然地想象为稀疏载体;例如，在面部识别中，组件可能会自然地映射到面部的部分。

稀疏的主成分会产生一种更简约、可解释的表示，清楚地强调哪些原始特征会导致样本之间的差异。

下面的示例说明了使用稀疏PCA从Olivetti面部数据集中提取的16个分量。 可以看出，正规化项如何引入许多零。此外，数据的自然结构导致非零系数垂直相邻。该模型并没有在数学上强制执行这一点：每个分量都是一个载体 \(h \in \mathbf{R}^{4096}\) ，并且除了在作为64 x64像素图像的人性化可视化期间之外，不存在垂直相邻的概念。下面所示的分量出现局部的事实是数据的固有结构的影响，这使得这种局部模式最小化重建误差。存在考虑到邻接和不同类型结构的稀疏诱导规范;请参见 [Jen09] 以审查此类方法。有关如何使用Sparse PCA的更多详细信息，请参阅下面的示例部分。

请注意，稀疏PCA问题有许多不同的公式。这里实现的是基于 [Mrl09] .所解决的优化问题是PCA问题（字典学习）， \(\ell_1\) 对组件的处罚：

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||V||_{1,1} \\ \text{subject to } & ||U_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{components}\end{split}\]

\(||.||_{\text{Fro}}\) 代表弗罗贝尼乌斯规范， \(||.||_{1,1}\) 代表逐项矩阵范数，其是矩阵中所有项的绝对值之和。稀疏诱导 \(||.||_{1,1}\) 当可用的训练样本很少时，矩阵规范还可以防止学习组件受到干扰。惩罚程度（以及稀疏性）可以通过超参数调整 alpha .较小的值会导致温和的正规化因式分解，而较大的值会将许多系数缩小为零。

备注

虽然本着在线算法的精神，班级 MiniBatchSparsePCA 不实现 partial_fit 因为该算法沿着特征方向在线，而不是样本方向在线。

示例

• Faces数据集分解

引用

[Mrl09]

"Online Dictionary Learning for Sparse Coding" J. Mairal，F. Bach，J. Ponce，G. Sapiro，2009年

[Jen09]

"Structured Sparse Principal Component Analysis" R.杰纳顿，G.奥博津斯基，F.巴赫，2009年

2.5.2. 核心主成分分析（kPCA）

2.5.2.1. 精确的核心PCA

KernelPCA 是PCA的扩展，通过使用内核实现非线性维度缩减（请参阅 成对指标、亲和力和核心 ) [Scholkopf1997]. 它有许多应用，包括去噪，压缩和结构化预测（内核依赖估计）。 KernelPCA 同时支持 transform 和 inverse_transform .

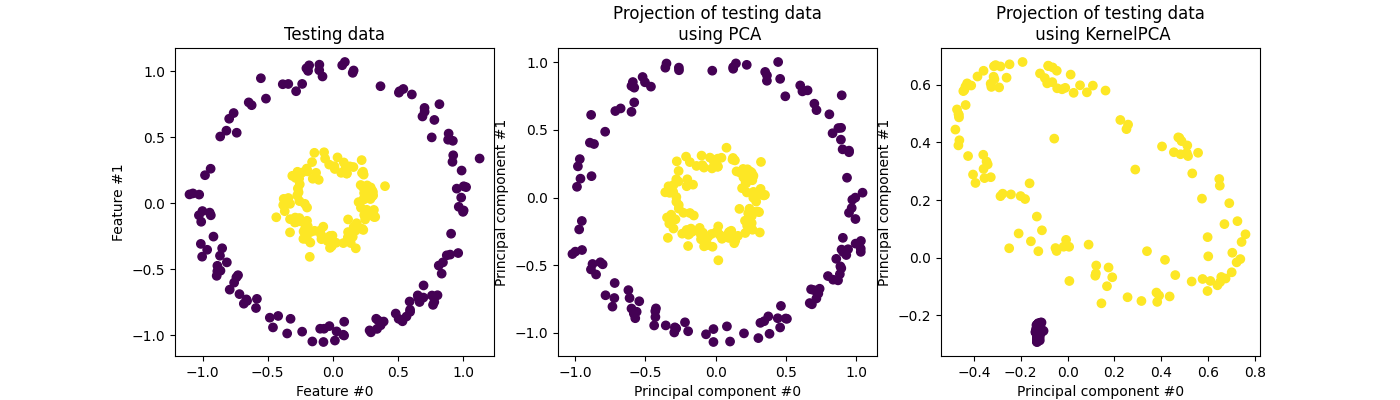
备注

KernelPCA.inverse_transform 依赖于核岭来学习将样本从PCA基础映射到原始特征空间的函数 [Bakir2003]. 因此，通过 KernelPCA.inverse_transform 是一个近似值。有关更多详细信息，请参阅下面链接的示例。

示例

• 核PCA

• 基于核主成分分析的图像去噪

引用

[Scholkopf1997]

肖尔科普夫、伯恩哈德、亚历山大·斯莫拉和克劳斯-罗伯特·穆勒。 "Kernel principal component analysis." 人工神经网络国际会议。施普林格，柏林，海德堡，1997年。

[Bakir2003]

Bakır，Gökhan H.，杰森·韦斯顿和伯恩哈德·肖尔科普夫。 "Learning to find pre-images." 神经信息处理系统的进展16（2003）：449-456。

2.5.2.2. 核PCA求解器的选择

而在 PCA 组件的数量由特征的数量限定， KernelPCA 成分的数量受到样本数量的限制。许多现实世界的数据集都有大量样本！在这些情况下，发现 all 具有完整kPCA的组件浪费了计算时间，因为数据主要由前几个组件描述（例如 n_components<=100 ).换句话说，在核心PCA匹配过程中进行特征分解的中心Gram矩阵的有效排序远小于其大小。在这种情况下，逼近特征解算器可以以非常低的精度损失提供加速。

特征解算器

可选参数 eigen_solver='randomized' 可用于 significantly 当请求的数量减少时，减少计算时间 n_components 与样本数量相比较小。它依靠随机分解方法在更短的时间内找到近似解。

The time complexity of the randomized KernelPCA is \(O(n_{\mathrm{samples}}^2 \cdot n_{\mathrm{components}})\) instead of \(O(n_{\mathrm{samples}}^3)\) for the exact method implemented with eigen_solver='dense'.

The memory footprint of randomized KernelPCA is also proportional to \(2 \cdot n_{\mathrm{samples}} \cdot n_{\mathrm{components}}\) instead of \(n_{\mathrm{samples}}^2\) for the exact method.

注：该技术与中相同 使用随机瓣膜分解的PCA .

除了上述两个求解器之外， eigen_solver='arpack' 可以用作获得近似分解的替代方法。在实践中，这种方法只在要查找的组件数量非常少时提供合理的执行时间。当所需的组件数小于10（严格）且样本数大于200（严格）时，默认情况下启用该选项。看到 KernelPCA 有关详细信息

引用

• dense 解算器： scipy.linalg.eigh documentation

• randomized 解算器：

  • 算法4.3中 "Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions" Halko等人（2009）

  • "An implementation of a randomized algorithm for principal component analysis" A. Szlam等人（2014）

• arpack 解算器： scipy.sparse.linalg.eigsh documentation R. B. Lehoucq，D. C.索伦森和C.杨，（1998）

2.5.3. 截短奇异值分解和潜在语义分析

TruncatedSVD 实现奇异值分解（MVD）的变体，仅计算 \(k\) 最大奇异值，其中 \(k\) 是用户指定的参数。

TruncatedSVD 非常类似于 PCA ，但不同之处在于矩阵 \(X\) 不需要集中。当列方向（每个特征）意味着 \(X\) 从特征值中减去，所得矩阵上的截断的奇异值相当于PCA。

关于截断的DID和潜在语义分析（LSA）

当截断的MVD应用于术语文档矩阵时（如由返回的 CountVectorizer 或 TfidfVectorizer ），这种转变被称为 latent semantic analysis (LSA)因为它将这些矩阵转换为低维的“语义”空间。特别是，LSA被认为可以对抗同义词和多义词的影响（这两者大致意味着每个单词有多个含义），这会导致术语-文档矩阵过于稀疏，并且在余弦相似性等度量下表现出较差的相似性。

备注

LSA也称为潜在语义索引、LSI，尽管严格来说，这是指其在持久索引中用于信息检索目的。

在数学上，应用于训练样本的截断的奇异值 \(X\) 产生低等级逼近 \(X\) :

\[X \近似X_k = U_k \Sigma_k V_k^\top\]

这次手术后， \(U_k \Sigma_k\) 是经过改造的训练集， \(k\) 功能（称为 n_components 在API中）。

还要转换测试集 \(X\) ，我们将其乘以 \(V_k\) :

\[X' = X V_k\]

备注

在自然语言处理（NLP）和信息检索（IR）文献中，大多数LSA的处理都交换矩阵的轴 \(X\) 以便它具有形状 (n_features, n_samples) .我们以不同的方式呈现LSA，更好地匹配scikit-learn API，但发现的奇异值是相同的。

而 TruncatedSVD Transformer适用于任何特征矩阵，建议在tf-idf矩阵上使用它，而不是LSA/文档处理设置中的原始频率计数。特别是，应打开次线性缩放和反向文档频率 (sublinear_tf=True, use_idf=True ）使特征值更接近高斯分布，从而补偿LSA对文本数据的错误假设。

示例

• 基于k-means的文本聚类

引用

• Christopher D. Manning，Prabhakar Raghavan and Hinrich Schütze（2008）， Introduction to Information Retrieval ，剑桥大学出版社，第18章： Matrix decompositions & latent semantic indexing

2.5.4. 字典学习

2.5.4.1. 使用预先计算的字典进行稀疏编码

的 SparseCoder 对象是一个估计器，可用于将信号转换为来自固定的、预先计算的字典（例如离散子波基）的原子的稀疏线性组合。因此，该对象不实现 fit 法这种转换相当于一个稀疏编码问题：将数据的表示形式视为尽可能少的字典原子的线性组合。字典学习的所有变体都实现以下转换方法，可通过 transform_method 初始化参数：

• 正交匹配追踪 (垂直匹配追求（OMP） )

• 最小角回归 (最小角回归 )

• 最小角回归计算套索

• 使用坐标下降的套索 (Lasso )

• 阈值化

格式保存非常快，但不会产生准确的重建。文献中已证明它们对于分类任务很有用。对于图像重建任务，垂直匹配追踪会产生最准确、最无偏差的重建。

字典学习对象通过 split_code 参数，分离稀疏编码结果中正值和负值的可能性。当字典学习用于提取将用于监督学习的特征时，这很有用，因为它允许学习算法为特定原子的负负载分配不同的权重，从到相应的正负载。

单个样本的拆分代码具有长度 2 * n_components 并使用以下规则构建：首先，常规长度代码 n_components 是计算的。然后第一 n_components 的条目 split_code 都填充有常规代码载体的正部分。拆分代码的后半部分填充了代码载体的负部分，只有正号。因此，split_code是非负的。

示例

• 使用预先计算的字典进行稀疏编码

2.5.4.2. 通用词典学习

字典学习 (DictionaryLearning ）是一个矩阵分解问题，相当于找到一个（通常是过完备的）字典，该字典将在稀疏编码拟合数据时表现良好。

哺乳动物初级视觉皮质的工作方式是将数据表示为来自过完整词典的原子稀疏组合。因此，应用于图像补丁的字典学习已被证明可以在图像完成、修复和去噪等图像处理任务以及监督识别任务中提供良好的结果。

字典学习是通过交替更新稀疏代码来解决的优化问题，作为多个Lasso问题的解决方案，考虑字典固定，然后更新字典以最佳地适应稀疏代码。

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||U||_{1,1} \\ \text{subject to } & ||V_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{\mathrm{atoms}}\end{split}\]

\(||.||_{\text{Fro}}\) 代表弗罗贝尼乌斯规范， \(||.||_{1,1}\) 代表逐项矩阵范数，其是矩阵中所有项的绝对值之和。使用这样的过程来适应字典后，转换只是一个稀疏编码步骤，与所有字典学习对象共享相同的实现（请参阅 使用预先计算的字典进行稀疏编码 ).

还可以将字典和/或代码约束为正，以匹配数据中可能存在的约束。以下是应用了不同积极性约束的面部。红色表示负值，蓝色表示正值，白色表示零。

下图显示了从浣熊脸的部分图像中提取的4x4像素图像块学习的字典的外观。

示例

• 使用字典学习的图像去噪

引用

• "Online dictionary learning for sparse coding" J. Mairal，F. Bach，J. Ponce，G. Sapiro，2009年

2.5.4.3. 小批量词典学习

MiniBatchDictionaryLearning 实现了更快、但不太准确的字典学习算法版本，该算法更适合大型数据集。

默认情况下， MiniBatchDictionaryLearning 将数据分为小批，并通过循环小批指定迭代次数来以在线方式进行优化。但是，目前它没有实现停止条件。

估计器还实现了 partial_fit ，它通过在迷你批处理上仅迭代一次来更新字典。当数据从一开始就不容易获得时，或者当数据不适合存储器时，这可以用于在线学习。

Clustering for dictionary learning

请注意，当使用字典学习来提取表示（例如对于稀疏编码）时，集群可以是学习字典的良好代理。比如 MiniBatchKMeans 估计器计算效率高，并通过 partial_fit 法

示例： 在线学习面部部分词典

2.5.5. 因子分析

在无监督学习中，我们只有一个数据集 \(X = \{x_1, x_2, \dots, x_n \}\) .如何用数学方式描述这个数据集？一个非常简单 continuous latent variable 模型 \(X\) 是

\[x_i = W h_i + \mo + \\]

The vector \(h_i\) is called "latent" because it is unobserved. \(\epsilon\) is considered a noise term distributed according to a Gaussian with mean 0 and covariance \(\Psi\) (i.e. \(\epsilon \sim \mathcal{N}(0, \Psi)\)), \(\mu\) is some arbitrary offset vector. Such a model is called "generative" as it describes how \(x_i\) is generated from \(h_i\). If we use all the \(x_i\)'s as columns to form a matrix \(\mathbf{X}\) and all the \(h_i\)'s as columns of a matrix \(\mathbf{H}\) then we can write (with suitably defined \(\mathbf{M}\) and \(\mathbf{E}\)):

\[\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}\]

换句话说我们 decomposed 矩阵 \(\mathbf{X}\) .

如果 \(h_i\) 给定时，上述方程自动暗示以下概率解释：

\[p（x_i| h_i）= \mathCal{N}（Wh_i + \mo，\Psi）\]

对于一个完整的概率模型，我们还需要潜在变量的先验分布 \(h\) .最简单的假设（基于高斯分布的良好属性）是 \(h \sim \mathcal{N}(0, \mathbf{I})\) . 这产生高斯作为的边际分布 \(x\) :

\[p（x）= \mathcal{N}（\mu，WW^T + \Psi）\]

现在，在没有任何进一步假设的情况下，拥有潜在变量的想法 \(h\) 将是多余的-- \(x\) 可以完全用平均值和协方差建模。我们需要对这两个参数之一施加一些更具体的结构。关于误差协方差的结构的一个简单的附加假设 \(\Psi\) :

• \(\Psi = \sigma^2 \mathbf{I}\) ：这个假设导致了 PCA .

• \(\Psi = \mathrm{diag}(\psi_1, \psi_2, \dots, \psi_n)\): This model is called FactorAnalysis, a classical statistical model. The matrix W is sometimes called the "factor loading matrix".

这两个模型本质上都是用低阶协方差矩阵估计高斯。由于这两个模型都是概率模型，因此它们可以集成到更复杂的模型中，例如因子分析器混合物。人们会得到非常不同的模型（例如 FastICA ）如果假设潜在变量的非高斯先验。

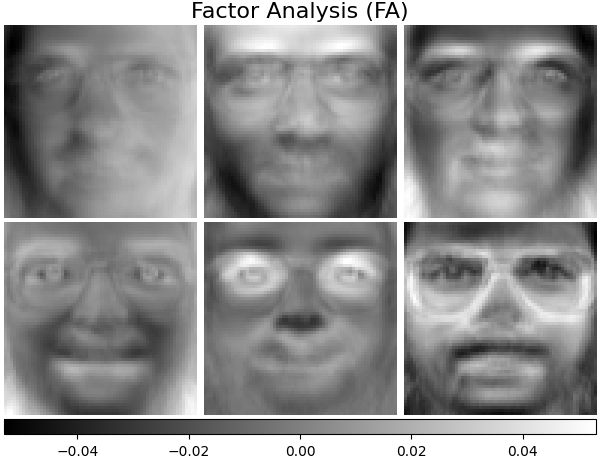
因子分析 can 产生类似的组件（其负载矩阵的列）， PCA .然而，人们无法对这些组件做出任何一般性声明（例如，它们是否是垂直的）：

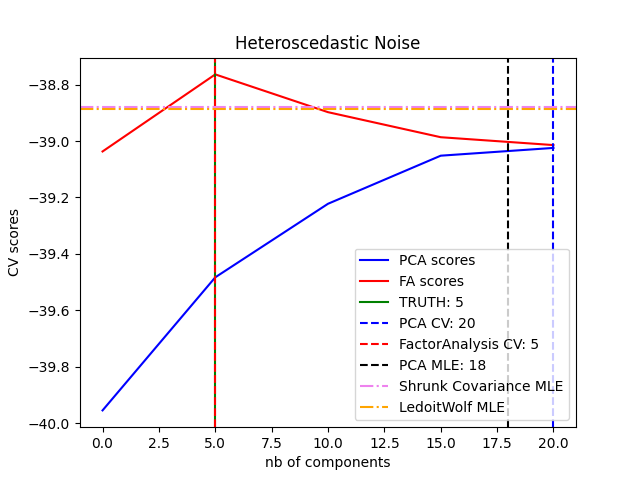
因子分析的主要优势 PCA 它可以独立地对输入空间每个方向的方差进行建模（异方差噪音）：

这允许在存在异方差噪音的情况下比概率PCA更好的模型选择：

因子分析之后通常会对因子进行旋转（参数 rotation ），通常是为了提高可解释性。例如，Varimax旋转使平方负载的方差之和最大化，即它往往会产生更稀疏的因素，每个因素只受少数特征（“简单结构”）的影响。例如，下面的第一个例子。

示例

• 因子分析（旋转）以可视化模式

• 使用概率PCA和因子分析（FA）进行模型选择

2.5.6. 独立成分分析（ICA）

独立分量分析将多元信号分离为最大独立的附加子分量。它是在scikit-learn中使用 Fast ICA 算法通常，ICA不用于降低维度，而是用于分离叠加信号。由于ICA模型不包括噪音项，因此为了使模型正确，必须应用白化。这可以在内部使用 whiten 参数或手动使用PCA变体之一。

它通常用于分离混合信号（称为 blind source separation ），如下面的例子所示：

ICA还可以用作另一种非线性分解，它可以找到具有一定稀疏性的组件：

示例

• 使用FastICA的盲源分离

• 2D点云上的FastICA

• Faces数据集分解

2.5.7. 非负矩阵分解（NMF或NNMF）

2.5.7.1. 具有弗罗贝尼乌斯规范的NMF

NMF [1] 是一种分解的替代方法，它假设数据和组件是非负的。 NMF 可以插入而不是 PCA 或其变体，在数据矩阵不包含负值的情况下。它发现样本的分解 \(X\) 为两个矩阵 \(W\) 和 \(H\) 通过优化距离来实现非负元素 \(d\) 之间 \(X\) 以及矩阵产品 \(WH\) .最广泛使用的距离函数是平方弗罗贝尼乌斯规范，它是欧几里得规范对矩阵的明显扩展：

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

Unlike PCA, the representation of a vector is obtained in an additive fashion, by superimposing the components, without subtracting. Such additive models are efficient for representing images and text.

已观察到 [Hoyer, 2004] [2] 当仔细限制时， NMF 可以生成基于零件的数据集表示，从而产生可解释的模型。下面的示例显示了由 NMF 根据Olivetti人脸数据集中的图像，与PCA特征脸进行比较。

的 init 属性决定应用的初始化方法，这对方法的性能有很大影响。 NMF 非负双奇异值分解方法Nonnegative Double Singular Value Decomposition NNDSVD [4] 基于两个奇异值分解过程，一个逼近数据矩阵，另一个利用单位阶矩阵的代数性质逼近所得部分奇异值分解因子的正部分。基本的NNDSDVD算法更适合稀疏因子分解。在密集情况下，推荐使用其变体NNDSVDa（其中所有零设置为等于数据所有元素的平均值）和NNDSVDar（其中零设置为小于数据平均值除以100的随机扰动）。

请注意，相乘更新（“ku”）解算器无法更新初始化中存在的零，因此当与引入大量零的基本NNSVD算法联合使用时，会导致更差的结果;在这种情况下，应该首选NNSVDa或NNSVDar。

NMF 还可以通过设置，用正确缩放的随机非负矩阵初始化 init="random" .整种子或 RandomState 也可以被传递到 random_state 以控制重现性。

In NMF, L1 and L2 priors can be added to the loss function in order to regularize the model. The L2 prior uses the Frobenius norm, while the L1 prior uses an elementwise L1 norm. As in ElasticNet, we control the combination of L1 and L2 with the l1_ratio (\(\rho\)) parameter, and the intensity of the regularization with the alpha_W and alpha_H (\(\alpha_W\) and \(\alpha_H\)) parameters. The priors are scaled by the number of samples (\(n\_samples\)) for H and the number of features (\(n\_features\)) for W to keep their impact balanced with respect to one another and to the data fit term as independent as possible of the size of the training set. Then the priors terms are:

\[(\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

而正规化目标函数是：

\[d_{\mathrm{Fro}}(X, WH) + (\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

2.5.7.2. 具有Beta偏差的NMF

如前所述，最广泛使用的距离函数是平方弗罗贝尼乌斯规范，它是欧几里得规范对矩阵的明显扩展：

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{Fro}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

其他距离函数可以在NMF中使用，例如（广义）Kullback-Leibler（KL）分歧，也称为I分歧：

\[d_{KL}（X，Y）= \sum_{i，j}（X_{aj} \log（\fRAC{X_{aj}}{Y_{aj}}）- X_{aj} + Y_{aj}）\]

或者，Itakura-Saito（IS）分歧：

\[d_{IS}(X, Y) = \sum_{i,j} (\frac{X_{ij}}{Y_{ij}} - \log(\frac{X_{ij}}{Y_{ij}}) - 1)\]

这三个距离是β发散族的特殊情况， \(\beta = 2, 1, 0\) 分别 [6]. Beta分歧的定义如下：

\[d_{\beta}(X, Y) = \sum_{i,j} \frac{1}{\beta(\beta - 1)}(X_{ij}^\beta + (\beta-1)Y_{ij}^\beta - \beta X_{ij} Y_{ij}^{\beta - 1})\]

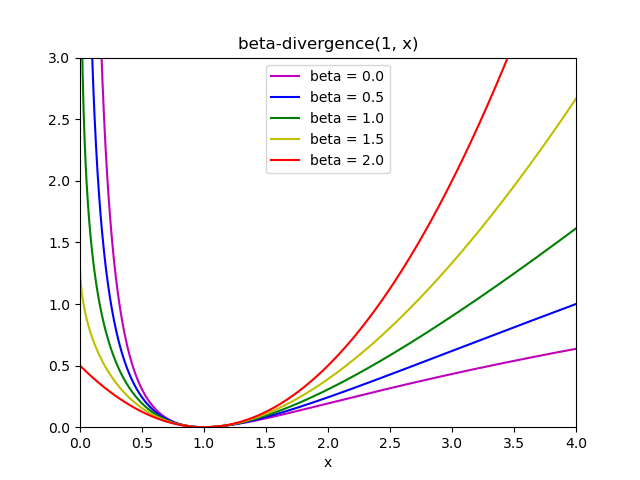
请注意，如果出现以下情况，则此定义无效 \(\beta \in (0; 1)\) ，但它可以不断扩展到 \(d_{KL}\) 和 \(d_{IS}\) 分别

NMF实施的求解器

NMF implements two solvers, using Coordinate Descent ('cd') [5], and Multiplicative Update ('mu') [6]. The 'mu' solver can optimize every beta-divergence, including of course the Frobenius norm (\(\beta=2\)), the (generalized) Kullback-Leibler divergence (\(\beta=1\)) and the Itakura-Saito divergence (\(\beta=0\)). Note that for \(\beta \in (1; 2)\), the 'mu' solver is significantly faster than for other values of \(\beta\). Note also that with a negative (or 0, i.e. 'itakura-saito') \(\beta\), the input matrix cannot contain zero values.

“cd”求解器只能优化Frobenius范数。由于NMF的潜在非凸性，即使在优化相同的距离函数时，不同的求解器也可能收敛到不同的最小值。

NMF最好与 fit_transform 方法，该方法返回矩阵W。矩阵H被存储到 components_ 属性;方法 transform 将基于这些存储的分量分解新矩阵X_new：：

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)

示例

• Faces数据集分解

• 非负矩阵分解和潜在Dirichlet分配的主题提取

2.5.7.3. 小批量非负矩阵分解

MiniBatchNMF [7] 实现更快但不太准确的非负矩阵分解版本（即 NMF ），更适合大型数据集。

默认情况下， MiniBatchNMF 将数据分为小批量，并通过循环小批量进行指定迭代次数，以在线方式优化NMF模型。的 batch_size 参数控制批的大小。

为了加速迷你批算法，还可以扩展过去的批，使它们的重要性低于新批。这是通过引入由 forget_factor 参数.

估计器还实现了 partial_fit ，它更新 H 通过在迷你批处理上仅迭代一次。当数据从一开始就不容易获得或数据不适合存储器时，这可以用于在线学习。

引用

[1]

"Learning the parts of objects by non-negative matrix factorization" D. Lee，S.承，1999年

[2]

"Non-negative Matrix Factorization with Sparseness Constraints" P. Hoyer，2004

[4]

"SVD based initialization: A head start for nonnegative matrix factorization" C.贝迪斯，E.加洛普洛斯，2008

[5]

"Fast local algorithms for large scale nonnegative matrix and tensor factorizations." A.西西斯基，A.潘，2009年

[6] (1,2)

"Algorithms for nonnegative matrix factorization with the beta-divergence" C. Fevotte，J. Idier，2011年

[7]

"Online algorithms for nonnegative matrix factorization with the Itakura-Saito divergence" A. Lefevre，F.巴赫，C.费沃特，2011年

2.5.8. 潜在狄利克雷分配（LDA）

潜在Dirichlet Allocation是一种针对文本库等离散数据集集合的生成概率模型。它也是一个主题模型，用于从文档集合中发现抽象主题。

LDA的图形模型是一个三级生成模型：

关于上面图形模型中呈现的符号的注释，可以在Hoffman等人（2013）中找到：

• 该文集是一个集合 \(D\) 证件

• 文档是一系列 \(N\) 话

• 有 \(K\) 文集中的主题。

• 这些方框代表重复采样。

在图形模型中，每个节点都是一个随机变量，并且在生成过程中发挥作用。带阴影的节点指示观察变量，未带阴影的节点指示隐藏（潜在）变量。在这种情况下，文集中的单词是我们观察到的唯一数据。潜变量决定了文集中主题的随机混合以及文档中单词的分布。LDA的目标是使用观察到的单词来推断隐藏的主题结构。

有关建模文本库的详细信息

在对文本库建模时，该模型假设如下的生成过程用于包含 \(D\) 文件和 \(K\) 主题，与 \(K\) 对应于 n_components 在API中：

1. For each topic \(k \in K\), draw \(\beta_k \sim \mathrm{Dirichlet}(\eta)\). This provides a distribution over the words, i.e. the probability of a word appearing in topic \(k\). \(\eta\) corresponds to topic_word_prior.

2. For each document \(d \in D\), draw the topic proportions \(\theta_d \sim \mathrm{Dirichlet}(\alpha)\). \(\alpha\) corresponds to doc_topic_prior.

3. 为每个单词 \(i\) 号文件所 \(d\) :

   1. 绘制主题作业 \(z_{di} \sim \mathrm{Multinomial} (\theta_d)\)

   2. 画出观察到的单词 \(w_{ij} \sim \mathrm{Multinomial} (\beta_{z_{di}})\)

对于参数估计，后验分布为：

\[p(z, \theta, \beta |w, \alpha, \eta) = \frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}\]

Since the posterior is intractable, variational Bayesian method uses a simpler distribution \(q(z,\theta,\beta | \lambda, \phi, \gamma)\) to approximate it, and those variational parameters \(\lambda\), \(\phi\), \(\gamma\) are optimized to maximize the Evidence Lower Bound (ELBO):

\[\log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=} E_{q}[\log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[\log\:q(z, \theta, \beta)]\]

Maximizing ELBO is equivalent to minimizing the Kullback-Leibler(KL) divergence between \(q(z,\theta,\beta)\) and the true posterior \(p(z, \theta, \beta |w, \alpha, \eta)\).

LatentDirichletAllocation 实现在线变分Bayes算法，并支持在线和批量更新方法。批处理方法在每次完整通过数据后更新变分变量，而在线方法则从迷你批处理数据点更新变分变量。

备注

尽管在线方法保证收敛到局部最佳点，但最佳点的质量和收敛速度可能取决于小批量大小和与学习率设置相关的属性。

当 LatentDirichletAllocation 应用于“文档-术语”矩阵，该矩阵将被分解为“主题-术语”矩阵和“文档-主题”矩阵。而“主题-术语”矩阵存储为 components_ 在该模型中，“文档-主题”矩阵可以从 transform 法

LatentDirichletAllocation 还实现 partial_fit 法当可以顺序提取数据时使用此功能。

示例

• 非负矩阵分解和潜在Dirichlet分配的主题提取

引用

• "Latent Dirichlet Allocation" D.布莱，A. Ng，M.约旦，2003年

• "Online Learning for Latent Dirichlet Allocation” M.霍夫曼，D.布莱，F.巴赫，2010

• "Stochastic Variational Inference" M.霍夫曼，D.布莱，C. Wang，J. Paisley，2013

• "The varimax criterion for analytic rotation in factor analysis" H. F.凯撒，1958年

另见 降维 使用邻域成分分析进行降维。