核PCA

此示例显示了主成分分析之间的差异 (PCA ）及其核心版本 (KernelPCA ).

一方面，我们表明 KernelPCA 能够找到线性分离它们的数据投影，而情况并非如此 PCA .

最后，我们表明，将这个投影倒置是一种逼近 KernelPCA ，虽然它与 PCA .

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

投影数据： PCA vs. KernelPCA

在本节中，我们展示了在使用主成分分析（PCA）投影数据时使用内核的优势。我们创建一个由两个嵌套圆圈组成的数据集。

from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(n_samples=1_000, factor=0.3, noise=0.05, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)

让我们首先快速查看生成的数据集。

import matplotlib.pyplot as plt

_, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(8, 4))

train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
train_ax.set_ylabel("Feature #1")
train_ax.set_xlabel("Feature #0")
train_ax.set_title("Training data")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
_ = test_ax.set_title("Testing data")

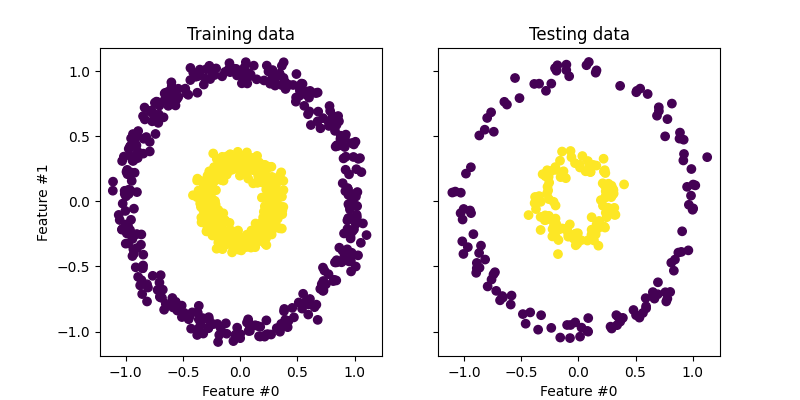
每个类别的样本不能线性分离：没有直线可以将内集的样本与外集的样本分开。

现在，我们将使用带有和不带有内核的PCA来了解使用这样的内核的效果。这里使用的核是辐射基函数（RBS）核。

from sklearn.decomposition import PCA, KernelPCA

pca = PCA(n_components=2)
kernel_pca = KernelPCA(
    n_components=None, kernel="rbf", gamma=10, fit_inverse_transform=True, alpha=0.1
)

X_test_pca = pca.fit(X_train).transform(X_test)
X_test_kernel_pca = kernel_pca.fit(X_train).transform(X_test)

fig, (orig_data_ax, pca_proj_ax, kernel_pca_proj_ax) = plt.subplots(
    ncols=3, figsize=(14, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Testing data")

pca_proj_ax.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c=y_test)
pca_proj_ax.set_ylabel("Principal component #1")
pca_proj_ax.set_xlabel("Principal component #0")
pca_proj_ax.set_title("Projection of testing data\n using PCA")

kernel_pca_proj_ax.scatter(X_test_kernel_pca[:, 0], X_test_kernel_pca[:, 1], c=y_test)
kernel_pca_proj_ax.set_ylabel("Principal component #1")
kernel_pca_proj_ax.set_xlabel("Principal component #0")
_ = kernel_pca_proj_ax.set_title("Projection of testing data\n using KernelPCA")

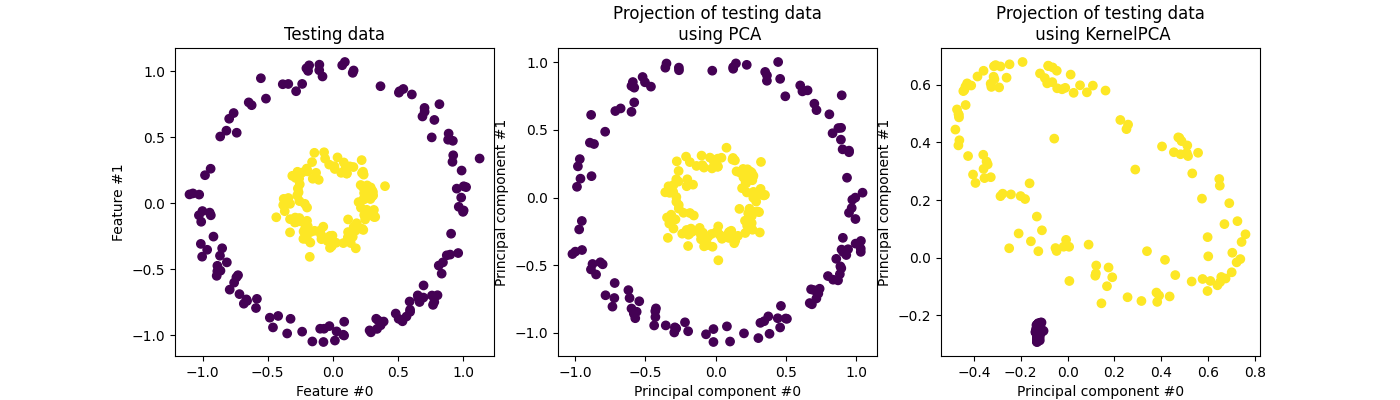
我们记得PCA线性转换数据。直观地说，这意味着坐标系将以每个组件为中心，根据其方差重新缩放，并最终旋转。从此转换中获得的数据是各向同性的，现在可以投影到其 principal components .

因此，查看使用PCA进行的投影（即中间的图），我们看到缩放没有变化;实际上，数据是两个以零为中心的同心圆，原始数据已经是各向同性的。但是，我们可以看到数据已经旋转。作为结论，我们看到，如果定义一个线性分类器来区分两个类的样本，这样的投影将没有帮助。

使用内核允许进行非线性投影。在这里，通过使用RBS核，我们预计投影将展开数据集，同时大致保持原始空间中彼此靠近的数据点对的相对距离。

我们在右图中观察到这种行为：给定类别的样本比来自相反类别的样本彼此更接近，从而解开了两个样本集。现在，我们可以使用线性分类器将样本从两个类别中分离出来。

投影到原始要素空间

使用时需要牢记的一个特殊性 KernelPCA 与重建（即原始特征空间中的反投影）有关。与 PCA ，重建将是准确的，如果 n_components 与原始功能的数量相同。本例中的情况就是如此。

我们可以调查在反投影时是否获得原始数据集 KernelPCA .

X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kernel_pca = kernel_pca.inverse_transform(kernel_pca.transform(X_test))

fig, (orig_data_ax, pca_back_proj_ax, kernel_pca_back_proj_ax) = plt.subplots(
    ncols=3, sharex=True, sharey=True, figsize=(13, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Original test data")

pca_back_proj_ax.scatter(X_reconstructed_pca[:, 0], X_reconstructed_pca[:, 1], c=y_test)
pca_back_proj_ax.set_xlabel("Feature #0")
pca_back_proj_ax.set_title("Reconstruction via PCA")

kernel_pca_back_proj_ax.scatter(
    X_reconstructed_kernel_pca[:, 0], X_reconstructed_kernel_pca[:, 1], c=y_test
)
kernel_pca_back_proj_ax.set_xlabel("Feature #0")
_ = kernel_pca_back_proj_ax.set_title("Reconstruction via KernelPCA")

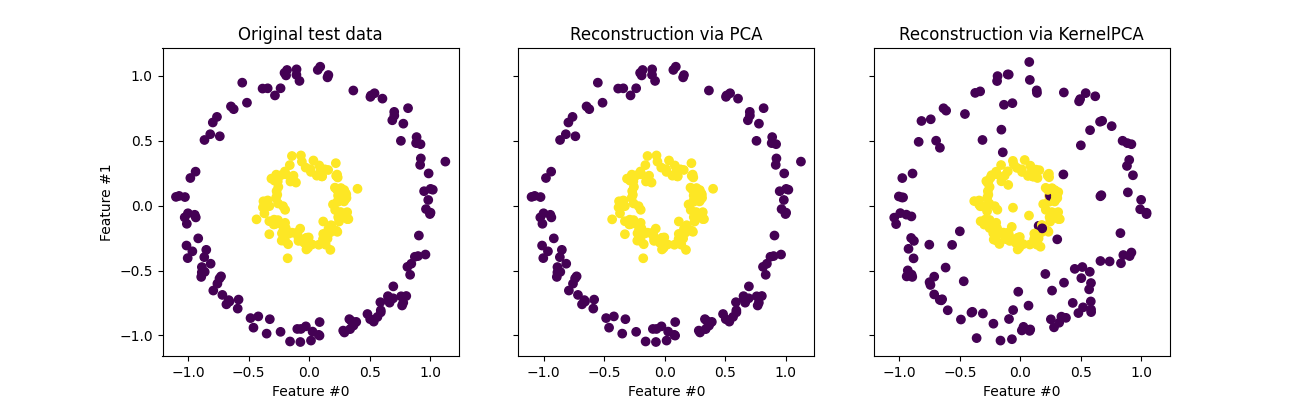
虽然我们看到了完美的重建， PCA 我们观察到不同的结果 KernelPCA .

事实上， inverse_transform 不能依赖于分析反投影，从而依赖于精确的重建。而是 KernelRidge 经过内部训练以学习从核心化PCA基础到原始特征空间的映射。因此，该方法具有一种在原始特征空间中反投影时引入小差异的逼近。

为了改善重建， inverse_transform ，可以调 alpha 在 KernelPCA ，控制映射训练期间对训练数据的依赖的正规化项。

相关实例

基于核主成分分析的图像去噪

Image denoising using kernel PCA

特征缩放的重要性

Importance of Feature Scaling

增量PCA

Incremental PCA

Faces数据集分解

Faces dataset decompositions