备注
Go to the end 下载完整的示例代码。或者通过浏览器中的MysterLite或Binder运行此示例
与时间相关的特征工程#
该笔记本电脑引入了不同的策略,以利用时间相关功能来执行高度依赖于业务周期(天、周、月)和年度季节周期的自行车共享需求回归任务。
在此过程中,我们介绍了如何使用 sklearn.preprocessing.SplineTransformer 阶级及其 extrapolation="periodic" 选项.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
自行车共享需求数据集的数据探索#
我们首先从OpenML存储库中加载数据。
from sklearn.datasets import fetch_openml
bike_sharing = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
df = bike_sharing.frame
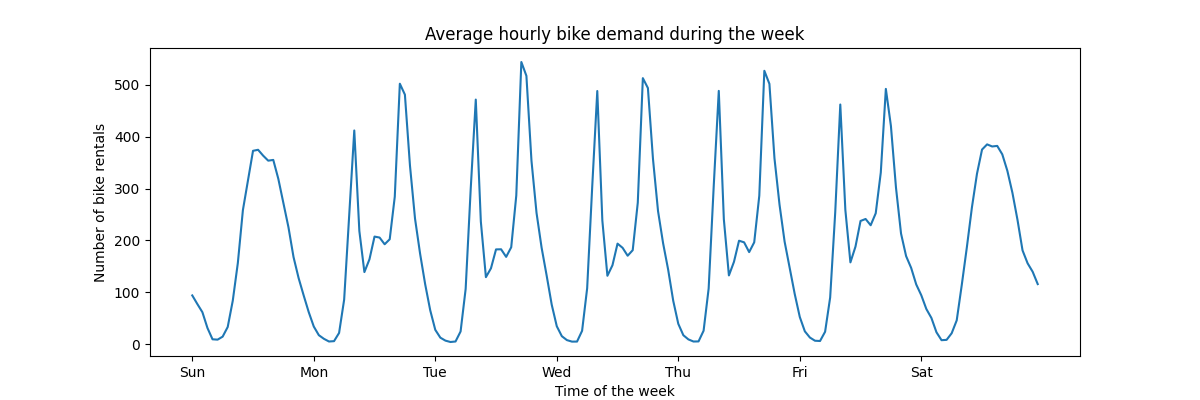
为了快速了解数据的周期模式,让我们看看一周内每小时的平均需求。
请注意,一周从周末的星期日开始。我们可以清楚地区分工作日早上和晚上的通勤模式和周末的自行车休闲使用,以及一天中间更分散的高峰需求:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="Average hourly bike demand during the week",
xticks=[i * 24 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week",
ylabel="Number of bike rentals",
)
预测问题的目标是按小时计算的自行车租赁的绝对数量:
df["count"].max()
np.int64(977)
让我们重新调整目标变量(每小时自行车租赁数量)来预测相对需求,以便平均绝对误差更容易解释为最大需求的一小部分。
备注
本笔记本中使用的模型的匹配方法都最小化了估计条件平均值的均方误差。然而,绝对误差将估计条件中位数。
然而,当在讨论中报告测试集的性能指标时,我们选择关注平均绝对误差而不是(根)均方误差,因为它更直观地解释。然而,请注意,在这项研究中,一个指标的最佳模型也是另一个指标的最佳模型。
y = df["count"] / df["count"].max()
fig, ax = plt.subplots(figsize=(12, 4))
y.hist(bins=30, ax=ax)
_ = ax.set(
xlabel="Fraction of rented fleet demand",
ylabel="Number of hours",
)
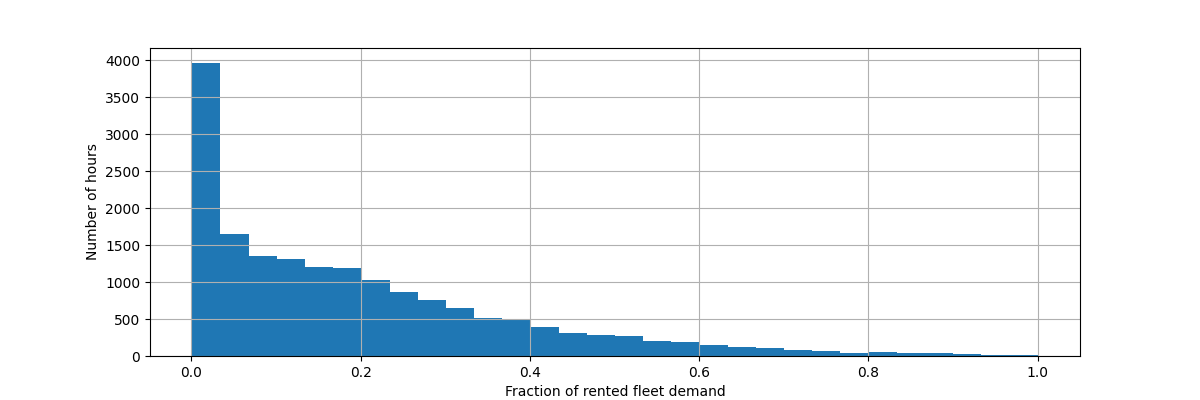
输入特征数据帧是描述天气条件的变量的时间注释每小时日志。它包括数字和类别变量。请注意,时间信息已经扩展为几个补充列。
X = df.drop("count", axis="columns")
X
| season | year | month | hour | holiday | weekday | workingday | weather | temp | feel_temp | humidity | windspeed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | spring | 0 | 1 | 0 | False | 6 | False | clear | 9.84 | 14.395 | 0.81 | 0.0000 |
| 1 | spring | 0 | 1 | 1 | False | 6 | False | clear | 9.02 | 13.635 | 0.80 | 0.0000 |
| 2 | spring | 0 | 1 | 2 | False | 6 | False | clear | 9.02 | 13.635 | 0.80 | 0.0000 |
| 3 | spring | 0 | 1 | 3 | False | 6 | False | clear | 9.84 | 14.395 | 0.75 | 0.0000 |
| 4 | spring | 0 | 1 | 4 | False | 6 | False | clear | 9.84 | 14.395 | 0.75 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | spring | 1 | 12 | 19 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | spring | 1 | 12 | 20 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | spring | 1 | 12 | 21 | False | 1 | True | clear | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | spring | 1 | 12 | 22 | False | 1 | True | clear | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | spring | 1 | 12 | 23 | False | 1 | True | clear | 10.66 | 13.635 | 0.65 | 8.9981 |
17379 rows × 12 columns
备注
如果时间信息仅以日期或日期时间列的形式存在,则我们可以使用pandas将其扩展为一天中的小时、一周中的天、一月中的一天、一年中的月份:https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#time-date-components
我们现在反思分类变量的分布,首先 "weather" :
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1419
heavy_rain 3
Name: count, dtype: int64
由于只有3个 "heavy_rain" 事件,我们不能使用此类别来训练具有交叉验证的机器学习模型。相反,我们通过将它们折叠到 "rain" 类别.
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1422
Name: count, dtype: int64
果然那 "season" 变量平衡良好:
X["season"].value_counts()
season
fall 4496
summer 4409
spring 4242
winter 4232
Name: count, dtype: int64
基于时间的交叉验证#
由于数据集是按时间顺序的事件日志(每小时需求),因此我们将使用时间敏感的交叉验证拆分器来尽可能真实地评估我们的需求预测模型。我们在列车和分裂的测试侧之间使用2天的间隔。我们还限制训练集大小,以使CV折叠的性能更加稳定。
1000个测试数据点应该足以量化模型的性能。这代表不到一个半月的连续测试数据:
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=5,
gap=48,
max_train_size=10000,
test_size=1000,
)
让我们手动检查各种拆分以检查 TimeSeriesSplit 正如我们预期的那样工作,从第一次拆分开始:
all_splits = list(ts_cv.split(X, y))
train_0, test_0 = all_splits[0]
X.iloc[test_0]
| season | year | month | hour | holiday | weekday | workingday | weather | temp | feel_temp | humidity | windspeed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12379 | summer | 1 | 6 | 0 | False | 2 | True | clear | 22.14 | 25.760 | 0.68 | 27.9993 |
| 12380 | summer | 1 | 6 | 1 | False | 2 | True | misty | 21.32 | 25.000 | 0.77 | 22.0028 |
| 12381 | summer | 1 | 6 | 2 | False | 2 | True | rain | 21.32 | 25.000 | 0.72 | 19.9995 |
| 12382 | summer | 1 | 6 | 3 | False | 2 | True | rain | 20.50 | 24.240 | 0.82 | 12.9980 |
| 12383 | summer | 1 | 6 | 4 | False | 2 | True | rain | 20.50 | 24.240 | 0.82 | 12.9980 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 13374 | fall | 1 | 7 | 11 | False | 1 | True | clear | 34.44 | 40.150 | 0.53 | 15.0013 |
| 13375 | fall | 1 | 7 | 12 | False | 1 | True | clear | 34.44 | 39.395 | 0.49 | 8.9981 |
| 13376 | fall | 1 | 7 | 13 | False | 1 | True | clear | 34.44 | 39.395 | 0.49 | 19.0012 |
| 13377 | fall | 1 | 7 | 14 | False | 1 | True | clear | 36.08 | 40.910 | 0.42 | 7.0015 |
| 13378 | fall | 1 | 7 | 15 | False | 1 | True | clear | 35.26 | 40.150 | 0.47 | 16.9979 |
1000 rows × 12 columns
X.iloc[train_0]
| season | year | month | hour | holiday | weekday | workingday | weather | temp | feel_temp | humidity | windspeed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2331 | summer | 0 | 4 | 1 | False | 2 | True | misty | 25.42 | 31.060 | 0.50 | 6.0032 |
| 2332 | summer | 0 | 4 | 2 | False | 2 | True | misty | 24.60 | 31.060 | 0.53 | 8.9981 |
| 2333 | summer | 0 | 4 | 3 | False | 2 | True | misty | 23.78 | 27.275 | 0.56 | 8.9981 |
| 2334 | summer | 0 | 4 | 4 | False | 2 | True | misty | 22.96 | 26.515 | 0.64 | 8.9981 |
| 2335 | summer | 0 | 4 | 5 | False | 2 | True | misty | 22.14 | 25.760 | 0.68 | 8.9981 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 12326 | summer | 1 | 6 | 19 | False | 6 | False | clear | 26.24 | 31.060 | 0.36 | 11.0014 |
| 12327 | summer | 1 | 6 | 20 | False | 6 | False | clear | 25.42 | 31.060 | 0.35 | 19.0012 |
| 12328 | summer | 1 | 6 | 21 | False | 6 | False | clear | 24.60 | 31.060 | 0.40 | 7.0015 |
| 12329 | summer | 1 | 6 | 22 | False | 6 | False | clear | 23.78 | 27.275 | 0.46 | 8.9981 |
| 12330 | summer | 1 | 6 | 23 | False | 6 | False | clear | 22.96 | 26.515 | 0.52 | 7.0015 |
10000 rows × 12 columns
我们现在检查最后的分裂:
train_4, test_4 = all_splits[4]
X.iloc[test_4]
| season | year | month | hour | holiday | weekday | workingday | weather | temp | feel_temp | humidity | windspeed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16379 | winter | 1 | 11 | 5 | False | 2 | True | misty | 13.94 | 16.665 | 0.66 | 8.9981 |
| 16380 | winter | 1 | 11 | 6 | False | 2 | True | misty | 13.94 | 16.665 | 0.71 | 11.0014 |
| 16381 | winter | 1 | 11 | 7 | False | 2 | True | clear | 13.12 | 16.665 | 0.76 | 6.0032 |
| 16382 | winter | 1 | 11 | 8 | False | 2 | True | clear | 13.94 | 16.665 | 0.71 | 8.9981 |
| 16383 | winter | 1 | 11 | 9 | False | 2 | True | misty | 14.76 | 18.940 | 0.71 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | spring | 1 | 12 | 19 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | spring | 1 | 12 | 20 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | spring | 1 | 12 | 21 | False | 1 | True | clear | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | spring | 1 | 12 | 22 | False | 1 | True | clear | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | spring | 1 | 12 | 23 | False | 1 | True | clear | 10.66 | 13.635 | 0.65 | 8.9981 |
1000 rows × 12 columns
X.iloc[train_4]
| season | year | month | hour | holiday | weekday | workingday | weather | temp | feel_temp | humidity | windspeed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6331 | winter | 0 | 9 | 9 | False | 1 | True | misty | 26.24 | 28.790 | 0.89 | 12.9980 |
| 6332 | winter | 0 | 9 | 10 | False | 1 | True | misty | 26.24 | 28.790 | 0.89 | 12.9980 |
| 6333 | winter | 0 | 9 | 11 | False | 1 | True | clear | 27.88 | 31.820 | 0.79 | 15.0013 |
| 6334 | winter | 0 | 9 | 12 | False | 1 | True | misty | 27.88 | 31.820 | 0.79 | 11.0014 |
| 6335 | winter | 0 | 9 | 13 | False | 1 | True | misty | 28.70 | 33.335 | 0.74 | 11.0014 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 16326 | winter | 1 | 11 | 0 | False | 0 | False | misty | 12.30 | 15.150 | 0.70 | 11.0014 |
| 16327 | winter | 1 | 11 | 1 | False | 0 | False | clear | 12.30 | 14.395 | 0.70 | 12.9980 |
| 16328 | winter | 1 | 11 | 2 | False | 0 | False | clear | 11.48 | 14.395 | 0.81 | 7.0015 |
| 16329 | winter | 1 | 11 | 3 | False | 0 | False | misty | 12.30 | 15.150 | 0.81 | 11.0014 |
| 16330 | winter | 1 | 11 | 4 | False | 0 | False | misty | 12.30 | 14.395 | 0.81 | 12.9980 |
10000 rows × 12 columns
一切都很好。我们现在准备好进行一些预测建模了!
梯度提升#
只要样本数量足够大,具有决策树的梯度增强回归通常足够灵活,可以有效地处理具有分类和数字特征混合的异类表格数据。
在这里,我们使用现代 HistGradientBoostingRegressor 原生支持分类功能。因此,我们只需要设置 categorical_features="from_dtype" 使得具有类别d类型的特征被认为是类别特征。作为参考,我们根据dype从金字塔中提取分类特征。内部树为这些功能使用专用的树拆分规则。
数值变量不需要预处理,为了简单起见,我们只尝试这个模型的默认超参数:
from sklearn.compose import ColumnTransformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import cross_validate
from sklearn.pipeline import make_pipeline
gbrt = HistGradientBoostingRegressor(categorical_features="from_dtype", random_state=42)
categorical_columns = X.columns[X.dtypes == "category"]
print("Categorical features:", categorical_columns.tolist())
Categorical features: ['season', 'holiday', 'workingday', 'weather']
让我们用5个基于时间的交叉验证拆分中的相对需求的平均绝对误差来评估我们的梯度提升模型:
import numpy as np
def evaluate(model, X, y, cv, model_prop=None, model_step=None):
cv_results = cross_validate(
model,
X,
y,
cv=cv,
scoring=["neg_mean_absolute_error", "neg_root_mean_squared_error"],
return_estimator=model_prop is not None,
)
if model_prop is not None:
if model_step is not None:
values = [
getattr(m[model_step], model_prop) for m in cv_results["estimator"]
]
else:
values = [getattr(m, model_prop) for m in cv_results["estimator"]]
print(f"Mean model.{model_prop} = {np.mean(values)}")
mae = -cv_results["test_neg_mean_absolute_error"]
rmse = -cv_results["test_neg_root_mean_squared_error"]
print(
f"Mean Absolute Error: {mae.mean():.3f} +/- {mae.std():.3f}\n"
f"Root Mean Squared Error: {rmse.mean():.3f} +/- {rmse.std():.3f}"
)
evaluate(gbrt, X, y, cv=ts_cv, model_prop="n_iter_")
Mean model.n_iter_ = 100.0
Mean Absolute Error: 0.044 +/- 0.003
Root Mean Squared Error: 0.068 +/- 0.005
我们看到我们设置了 max_iter 大到足以提前停止。
该模型的平均误差约为最大需求的4%至5%。这对于没有任何超参数调整的第一次试验来说非常好!我们只需要明确分类变量即可。请注意,与时间相关的特征按原样传递,即不处理它们。但对于基于树的模型来说,这不是什么大问题,因为它们可以学习有序输入特征和目标之间的非单调关系。
线性回归模型的情况并非如此,正如我们将在下文中看到的那样。
天真的线性回归#
与线性模型一样,类别变量需要进行一热编码。为了保持一致性,我们使用 MinMaxScaler ,尽管在这种情况下,它不会对结果产生太大影响,因为它们已经具有可比的规模:
from sklearn.linear_model import RidgeCV
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
one_hot_encoder = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
alphas = np.logspace(-6, 6, 25)
naive_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(
naive_linear_pipeline, X, y, cv=ts_cv, model_prop="alpha_", model_step="ridgecv"
)
Mean model.alpha_ = 2.7298221281347037
Mean Absolute Error: 0.142 +/- 0.014
Root Mean Squared Error: 0.184 +/- 0.020
看到被选中的人是肯定的 alpha_ 在我们的规定范围内。
性能不佳:平均误差在最大需求的14%左右。这比梯度增强模型的平均误差高出三倍多。我们可以怀疑,周期性时间相关特征的原始编码(只是最小-最大缩放)可能会阻止线性回归模型正确利用时间信息:线性回归不会自动建模输入特征和目标之间的非单调关系。必须在输入中设计非线性项。
例如, "hour" 该功能阻止线性模型认识到,早上从6点增加到8点应该会对自行车租赁数量产生强烈的积极影响,而晚上从18点增加到20点类似幅度的增加应该会对自行车租赁的预测数量产生强烈的负面影响。
时间步骤类别#
由于时间特征是以离散的方式编码的(“小时”特征中有24个唯一值),因此我们可以决定使用一热编码将这些特征视为分类变量,从而忽略小时值的顺序所暗示的任何假设。
对时间特征使用一次性编码为线性模型提供了更大的灵活性,因为我们在每个离散时间级别引入了一个额外的特征。
one_hot_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.099 +/- 0.011
Root Mean Squared Error: 0.131 +/- 0.011
该模型的平均错误率为10%,比使用时间特征的原始(有序)编码要好得多,这证实了我们的直觉,即线性回归模型受益于额外的灵活性,不会以单调的方式处理时间进程。
然而,这引入了大量的新功能。如果一天中的时间用一天开始后的分钟而不是小时来表示,那么一次性编码将引入1440个特征而不是24个特征。这可能会导致一些显着的过度装配。为了避免这种情况,我们可以使用 sklearn.preprocessing.KBinsDiscretizer 而是重新分类细粒度有序或数字变量的级别数量,同时仍然受益于一热编码的非单调表达优势。
最后,我们还观察到,单热编码完全忽略了小时级别的顺序,而这可能是一个有趣的归纳偏差,需要保留到一定程度。在下文中,我们尝试探索局部保留时间特征相对顺序的平滑、非单调编码。
三角特征#
作为第一次尝试,我们可以尝试使用具有匹配周期的sin和cos变换来编码这些周期特征中的每一个。
每个有序时间特征被转换成2个特征,这2个特征以非单调的方式一起编码等效信息,更重要的是,在周期范围的第一个值和最后一个值之间没有任何跳跃。
from sklearn.preprocessing import FunctionTransformer
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
让我们通过对hour=23的一点外推来可视化这种特征扩展对一些合成小时数据的影响:
import pandas as pd
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("Trigonometric encoding for the 'hour' feature")
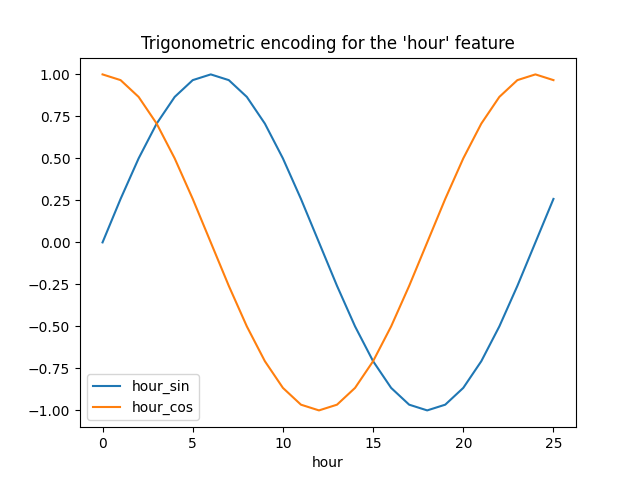
让我们使用将小时编码为颜色的2D散点图,以更好地了解这种表示如何将一天中的24小时映射到2D空间,类似于某种24小时版本的模拟时钟。请注意,由于sin/cos表示的周期性,“第25”小时被映射回第1小时。
fig, ax = plt.subplots(figsize=(7, 5))
sp = ax.scatter(hour_df["hour_sin"], hour_df["hour_cos"], c=hour_df["hour"])
ax.set(
xlabel="sin(hour)",
ylabel="cos(hour)",
)
_ = fig.colorbar(sp)
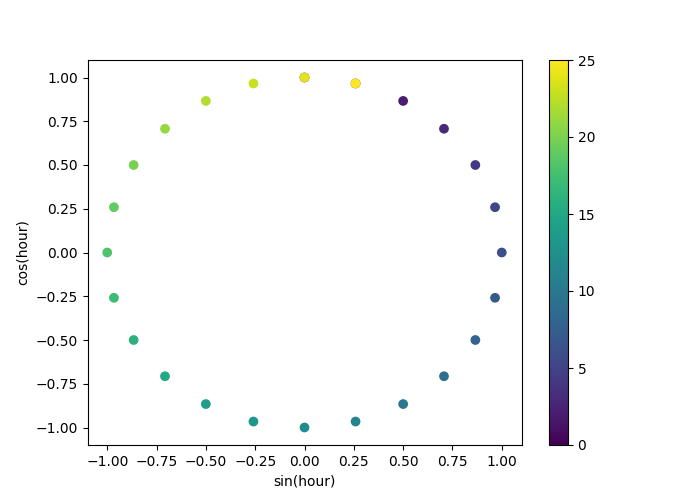
我们现在可以使用以下策略构建特征提取管道:
cyclic_cossin_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("month_sin", sin_transformer(12), ["month"]),
("month_cos", cos_transformer(12), ["month"]),
("weekday_sin", sin_transformer(7), ["weekday"]),
("weekday_cos", cos_transformer(7), ["weekday"]),
("hour_sin", sin_transformer(24), ["hour"]),
("hour_cos", cos_transformer(24), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_cossin_linear_pipeline = make_pipeline(
cyclic_cossin_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_cossin_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.125 +/- 0.014
Root Mean Squared Error: 0.166 +/- 0.020
采用这种简单特征工程的线性回归模型的性能比使用原始有序时间特征好一些,但比使用单一热编码时间特征差一些。我们将在本笔记本的最后进一步分析造成这一令人失望结果的可能原因。
周期样条曲线特征#
我们可以尝试使用具有足够多样条线数量的样条线变换来对周期性时间相关特征进行替代编码,因此与sin/cos变换相比,扩展特征数量更多:
from sklearn.preprocessing import SplineTransformer
def periodic_spline_transformer(period, n_splines=None, degree=3):
if n_splines is None:
n_splines = period
n_knots = n_splines + 1 # periodic and include_bias is True
return SplineTransformer(
degree=degree,
n_knots=n_knots,
knots=np.linspace(0, period, n_knots).reshape(n_knots, 1),
extrapolation="periodic",
include_bias=True,
)
再次,让我们通过小时=23以外的一点外推来想象这种特征扩展对一些合成小时数据的影响:
hour_df = pd.DataFrame(
np.linspace(0, 26, 1000).reshape(-1, 1),
columns=["hour"],
)
splines = periodic_spline_transformer(24, n_splines=12).fit_transform(hour_df)
splines_df = pd.DataFrame(
splines,
columns=[f"spline_{i}" for i in range(splines.shape[1])],
)
pd.concat([hour_df, splines_df], axis="columns").plot(x="hour", cmap=plt.cm.tab20b)
_ = plt.title("Periodic spline-based encoding for the 'hour' feature")
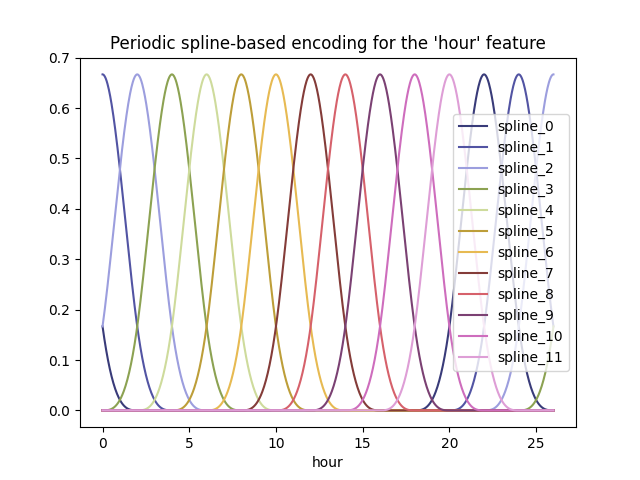
由于使用了 extrapolation="periodic" 参数,我们观察到当外推到午夜之后时,特征编码保持平滑。
我们现在可以使用这种替代周期性特征工程策略构建预测管道。
对于这些有序值,可以使用比离散级别更少的样条线。这使得基于样条曲线的编码比单热编码更有效,同时保留了大部分表现力:
cyclic_spline_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("cyclic_month", periodic_spline_transformer(12, n_splines=6), ["month"]),
("cyclic_weekday", periodic_spline_transformer(7, n_splines=3), ["weekday"]),
("cyclic_hour", periodic_spline_transformer(24, n_splines=12), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_spline_linear_pipeline = make_pipeline(
cyclic_spline_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.097 +/- 0.011
Root Mean Squared Error: 0.132 +/- 0.013
样条曲线特征使线性模型能够成功利用周期性时间相关特征,并将误差从最大需求的~14%降低到~10%,这与我们观察到的一次性编码特征类似。
特征对线性模型预测影响的定性分析#
在这里,我们想要可视化特征工程选择对预测的时间相关形状的影响。
为了做到这一点,我们考虑一个任意的基于时间的分割,以比较一系列数据点上的预测。
naive_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
naive_linear_predictions = naive_linear_pipeline.predict(X.iloc[test_0])
one_hot_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_linear_predictions = one_hot_linear_pipeline.predict(X.iloc[test_0])
cyclic_cossin_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_cossin_linear_predictions = cyclic_cossin_linear_pipeline.predict(X.iloc[test_0])
cyclic_spline_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_linear_predictions = cyclic_spline_linear_pipeline.predict(X.iloc[test_0])
我们通过放大测试集的最后96小时(4天)来可视化这些预测,以获得一些定性见解:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by linear models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(naive_linear_predictions[last_hours], "x-", label="Ordinal time features")
ax.plot(
cyclic_cossin_linear_predictions[last_hours],
"x-",
label="Trigonometric time features",
)
ax.plot(
cyclic_spline_linear_predictions[last_hours],
"x-",
label="Spline-based time features",
)
ax.plot(
one_hot_linear_predictions[last_hours],
"x-",
label="One-hot time features",
)
_ = ax.legend()

从上面的图中我们可以得出以下结论:
的 raw ordinal time-related features 存在问题,因为它们没有捕捉到自然周期性:当小时特征从23回到0时,我们观察到每天结束时,预测会出现大幅跳跃。我们可以期待在每周或每年结束时都会出现类似的文物。
果然那 trigonometric features (sine和cos)在午夜时不存在这些不连续性,但线性回归模型未能利用这些特征来正确地建模日内变化。使用高次次
的 periodic spline-based features 一次解决这两个问题:通过使用12个样条线,它们可以专注于特定的时间,从而为线性模型提供了更多的表达力。此外
extrapolation="periodic"选项强制实现之间的平滑表示hour=23和hour=0.的 one-hot encoded features 其行为类似于基于样条曲线的周期性特征,但更尖锐:例如,它们可以更好地模拟工作日的早晨峰值,因为该峰值持续时间短于一小时。然而,我们将在下文中看到,线性模型的优势不一定是更具表达力的模型的优势。
我们还可以比较每个特征工程管道提取的特征数量:
naive_linear_pipeline[:-1].transform(X).shape
(17379, 19)
one_hot_linear_pipeline[:-1].transform(X).shape
(17379, 59)
cyclic_cossin_linear_pipeline[:-1].transform(X).shape
(17379, 22)
cyclic_spline_linear_pipeline[:-1].transform(X).shape
(17379, 37)
这证实了one-hot编码和样条编码策略为时间表示创建了比替代方案更多的特征,这反过来又为下游线性模型提供了更大的灵活性(自由度),以避免欠拟合。
最后,我们观察到,没有一个线性模型可以近似真实的自行车租赁需求,特别是对于工作日高峰时段可能非常尖锐但周末时段可能要平坦得多的高峰:基于样条线或单热编码的最准确线性模型往往会预测与交通相关的自行车租赁的峰值,甚至在周末,并低估了通勤-工作日期间的相关事件。
这些系统性预测错误揭示了一种欠拟的形式,可以通过特征(例如“工作日”和源自“小时”的特征)之间缺乏交互项来解释。此问题将在下一节中解决。
利用样条和多项特征建模成对相互作用#
线性模型不会自动捕获输入要素之间的交互效应。某些要素是边缘非线性的,这并没有帮助,例如由 SplineTransformer (or一次性编码或分类)。
但是,可以使用 PolynomialFeatures 粗粒度样条编码小时的类,以显式地建模“工作日”/“小时”交互作用,而不会引入太多新变量:
from sklearn.pipeline import FeatureUnion
from sklearn.preprocessing import PolynomialFeatures
hour_workday_interaction = make_pipeline(
ColumnTransformer(
[
("cyclic_hour", periodic_spline_transformer(24, n_splines=8), ["hour"]),
("workingday", FunctionTransformer(lambda x: x == "True"), ["workingday"]),
]
),
PolynomialFeatures(degree=2, interaction_only=True, include_bias=False),
)
然后将这些特征与之前的样条曲线基管道中已经计算的特征相结合。通过显式地建模这种成对交互,我们可以观察到良好的性能改进:
cyclic_spline_interactions_pipeline = make_pipeline(
FeatureUnion(
[
("marginal", cyclic_spline_transformer),
("interactions", hour_workday_interaction),
]
),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_interactions_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.078 +/- 0.009
Root Mean Squared Error: 0.104 +/- 0.009
建模与核的非线性特征交互#
之前的分析强调了对之间的相互作用进行建模的必要性 "workingday" 和 "hours" .我们想要建模的这种非线性相互作用的另一个例子可能是降雨的影响,例如,在工作日、周末和假期期间,降雨的影响可能不一样。
为了对所有此类相互作用进行建模,我们可以在基于样条曲线的扩展之后,同时对所有边缘特征使用一次多项扩展。然而,这会创建二次数量的特征,这可能会导致过拟和计算可处理性问题。
或者,我们可以使用Nyström方法来计算近似的多项核展开。让我们尝试后者:
from sklearn.kernel_approximation import Nystroem
cyclic_spline_poly_pipeline = make_pipeline(
cyclic_spline_transformer,
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.053 +/- 0.002
Root Mean Squared Error: 0.076 +/- 0.004
我们观察到,该模型几乎可以与梯度增强树的性能相媲美,平均误差约为最大需求的5%。
请注意,虽然该管道的最后一步是线性回归模型,但中间步骤(如样条特征提取和Nyström核近似)是高度非线性的。因此,复合管道比具有原始特征的简单线性回归模型更具表现力。
为了完整性起见,我们还评估了一热编码和内核逼近的组合:
one_hot_poly_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder="passthrough",
),
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.082 +/- 0.006
Root Mean Squared Error: 0.111 +/- 0.011
虽然在使用线性模型时,一次性编码特征与基于样条曲线的特征具有竞争力,但在使用非线性核的低阶逼近时情况不再是这样:这可以通过样条曲线特征更平滑并允许核逼近来找到更具表达力的决策函数这一事实来解释。
现在让我们定性地看看核模型和梯度增强树的预测,这些树应该能够更好地建模特征之间的非线性相互作用:
gbrt.fit(X.iloc[train_0], y.iloc[train_0])
gbrt_predictions = gbrt.predict(X.iloc[test_0])
one_hot_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_poly_predictions = one_hot_poly_pipeline.predict(X.iloc[test_0])
cyclic_spline_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_poly_predictions = cyclic_spline_poly_pipeline.predict(X.iloc[test_0])
我们再次放大测试集的最后4天:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by non-linear regression models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
gbrt_predictions[last_hours],
"x-",
label="Gradient Boosted Trees",
)
ax.plot(
one_hot_poly_predictions[last_hours],
"x-",
label="One-hot + polynomial kernel",
)
ax.plot(
cyclic_spline_poly_predictions[last_hours],
"x-",
label="Splines + polynomial kernel",
)
_ = ax.legend()
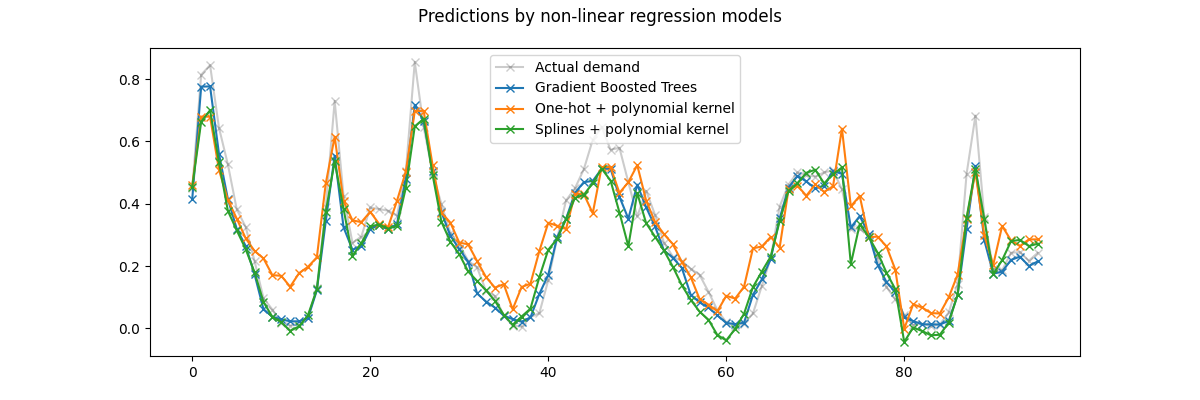
首先,请注意,树可以自然地对非线性特征交互进行建模,因为默认情况下,决策树允许生长超过2个级别的深度。
在这里,我们可以观察到样条特征和非线性核的组合效果非常好,几乎可以与梯度增强回归树的准确性相媲美。
相反,单热编码时间特征在低等级核模型中表现不佳。特别是,它们比竞争车型明显高估了低需求时数。
我们还观察到,没有一个模型能够成功预测工作日高峰时段的一些峰值租金。可能需要访问其他功能才能进一步提高预测的准确性。例如,在任何时间点访问车队的地理重新划分或因需要维修而无法移动的自行车比例可能很有用。
最后,让我们使用真实需求与预测需求散点图来更定量地了解这三个模型的预测误差:
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(13, 7), sharex=True, sharey="row")
fig.suptitle("Non-linear regression models", y=1.0)
predictions = [
one_hot_poly_predictions,
cyclic_spline_poly_predictions,
gbrt_predictions,
]
labels = [
"One hot +\npolynomial kernel",
"Splines +\npolynomial kernel",
"Gradient Boosted\nTrees",
]
plot_kinds = ["actual_vs_predicted", "residual_vs_predicted"]
for axis_idx, kind in enumerate(plot_kinds):
for ax, pred, label in zip(axes[axis_idx], predictions, labels):
disp = PredictionErrorDisplay.from_predictions(
y_true=y.iloc[test_0],
y_pred=pred,
kind=kind,
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set_xticks(np.linspace(0, 1, num=5))
if axis_idx == 0:
ax.set_yticks(np.linspace(0, 1, num=5))
ax.legend(
["Best model", label],
loc="upper center",
bbox_to_anchor=(0.5, 1.3),
ncol=2,
)
ax.set_aspect("equal", adjustable="box")
plt.show()
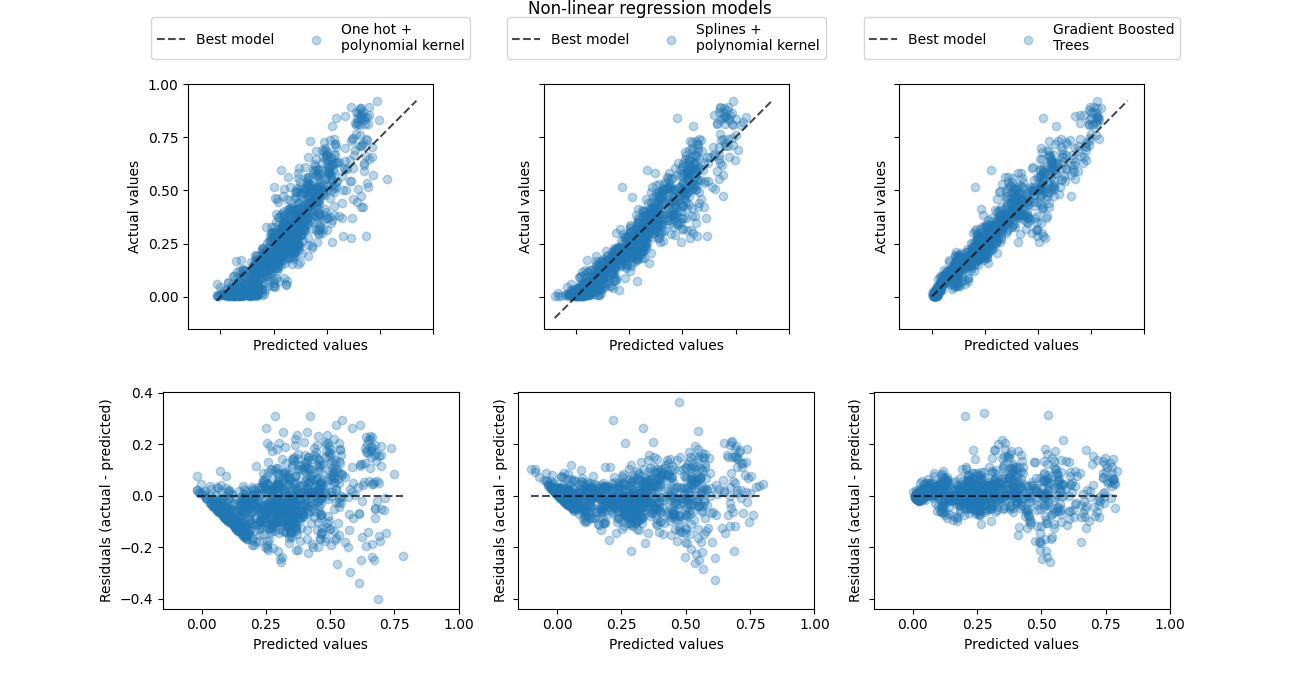
这个可视化证实了我们根据之前的情节得出的结论。
所有模型都低估了高需求事件(工作日高峰时间),但梯度提升的影响较小。平均而言,通过梯度提升可以很好地预测低需求事件,而单一的多元回归管道似乎系统性地高估了该制度下的需求。总体而言,梯度增强树的预测比核心模型更接近对角线。
总结发言#
我们注意到,通过使用更多组件(更高等级的核逼近),我们本可以以更长的适应和预测持续时间为代价,为核模型获得稍好的结果。对于较大的 n_components ,单热编码特征的性能甚至会匹配样条线特征。
的 Nystroem + RidgeCV 回归量也可以被替换为 MLPRegressor 有一两个隐藏层,我们会得到非常相似的结果。
我们在本案例研究中使用的数据集是以小时为基础进行采样的。然而,基于循环样条的特征可以通过更细粒度的时间分辨率(例如,每分钟而不是每小时进行测量)非常有效地对一天内的时间或一周内的时间进行建模,而无需引入更多的特征。独热编码时间表示将不提供这种灵活性。
最后,在我们使用的这个笔记本中 RidgeCV 因为从计算的角度来看,它非常高效。然而,它将目标变量建模为具有恒定方差的高斯随机变量。对于正回归问题,使用Poisson或Gamma分布可能更有意义。这可以通过使用来实现 GridSearchCV(TweedieRegressor(power=2), param_grid({"alpha": alphas})) 而不是 RidgeCV .
Total running time of the script: (0分15.488秒)
相关实例
Gallery generated by Sphinx-Gallery <https://sphinx-gallery.github.io> _