核岭回归与高斯过程回归的比较

此示例说明了核岭回归和高斯过程回归之间的差异。

核岭回归和高斯过程回归都在使用所谓的“核技巧”来使其模型具有足够的表达力以适应训练数据。然而，这两种方法解决的机器学习问题截然不同。

核岭回归将找到最小化损失函数（均方误差）的目标函数。

高斯过程回归采用概率方法，而不是寻找单个目标函数：目标函数上的高斯后验分布是基于Bayes定理定义的，因此目标函数上的先验概率与由观察到的训练数据定义的似然函数相结合，以提供后验分布的估计。

我们将通过一个例子来说明这些差异，并且还将重点关注调整内核超参数。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

生成数据集

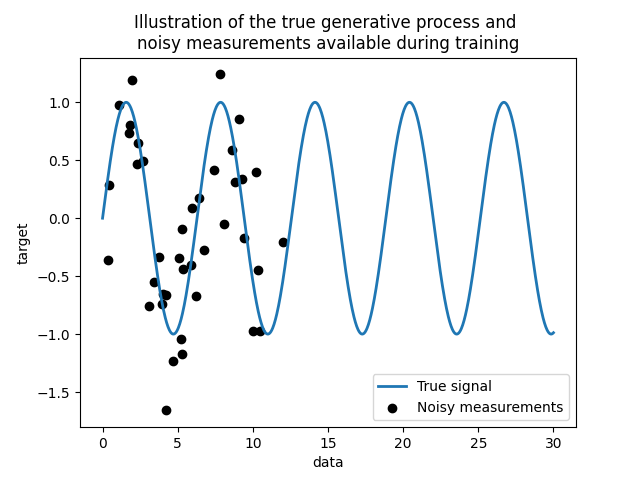
我们创建一个合成数据集。真正的生成过程将获取一个1-D载体并计算其sin。请注意，该sin的周期因此为 \(2 \pi\) .我们将在本示例的后面重新使用此信息。

import numpy as np

rng = np.random.RandomState(0)
data = np.linspace(0, 30, num=1_000).reshape(-1, 1)
target = np.sin(data).ravel()

现在，我们可以想象一种场景，我们从这个真实过程中获得观察。然而，我们将添加一些挑战：

• 测量结果会有噪音;

• 只有信号开始时的样本才可用。

training_sample_indices = rng.choice(np.arange(0, 400), size=40, replace=False)
training_data = data[training_sample_indices]
training_noisy_target = target[training_sample_indices] + 0.5 * rng.randn(
    len(training_sample_indices)
)

让我们绘制真实信号和可用于训练的噪音测量值。

import matplotlib.pyplot as plt

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Illustration of the true generative process and \n"
    "noisy measurements available during training"
)

简单线性模型的局限性

首先，我们想强调给定我们的数据集线性模型的局限性。我们适合 Ridge 并在我们的数据集上检查这个模型的预测。

from sklearn.linear_model import Ridge

ridge = Ridge().fit(training_data, training_noisy_target)

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(data, ridge.predict(data), label="Ridge regression")
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Limitation of a linear model such as ridge")

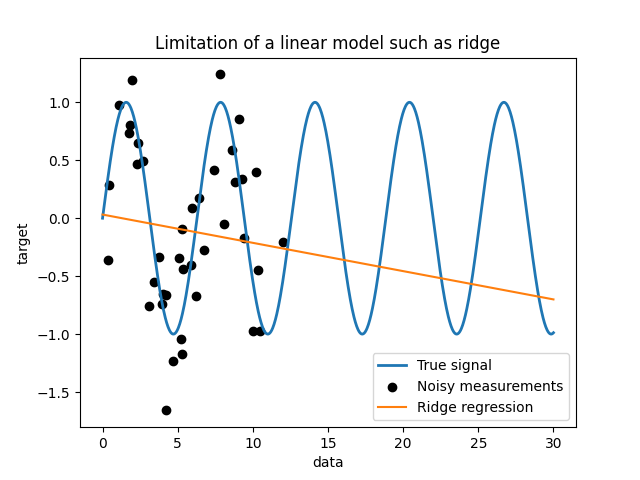
这样的岭回归量不适合数据，因为它没有足够的表现力。

核方法：核岭和高斯过程

核岭

我们可以通过使用所谓的内核使之前的线性模型更具表现力。核是从原始特征空间到另一个特征空间的嵌入。简而言之，它用于将我们的原始数据映射到更新、更复杂的特征空间。这个新空间由内核的选择显式定义。

在我们的例子中，我们知道真正的生成过程是一个周期函数。我们可以使用一个 ExpSineSquared 允许恢复周期性的内核。类 KernelRidge 会接受这样的内核。

将此模型与内核一起使用相当于使用内核的映射函数嵌入数据，然后应用岭回归。在实践中，数据不会被显式映射;相反，使用“核技巧”计算更高维度特征空间中样本之间的点积。

因此，让我们使用这样一个 KernelRidge .

import time

from sklearn.gaussian_process.kernels import ExpSineSquared
from sklearn.kernel_ridge import KernelRidge

kernel_ridge = KernelRidge(kernel=ExpSineSquared())

start_time = time.time()
kernel_ridge.fit(training_data, training_noisy_target)
print(
    f"Fitting KernelRidge with default kernel: {time.time() - start_time:.3f} seconds"
)

Fitting KernelRidge with default kernel: 0.001 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    kernel_ridge.predict(data),
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using default hyperparameters"
)

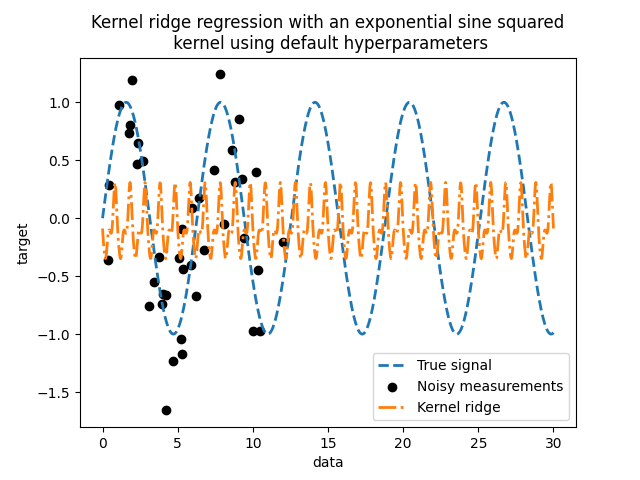
这个贴合的模型并不准确。事实上，我们没有设置内核的参数，而是使用默认参数。我们可以检查它们。

kernel_ridge.kernel

ExpSineSquared(length_scale=1, periodicity=1)

我们的内核有两个参数：长度规模和周期性。对于我们的数据集，我们使用 sin 作为生成过程，意味着 \(2 \pi\) - 信号的周期性。参数的默认值为 \(1\) ，它解释了我们模型的预测中观察到的高频。使用长度尺度参数也可以得出类似的结论。因此，它告诉我们需要调整内核参数。我们将使用随机搜索来调整核心岭模型的不同参数： alpha 参数和内核参数。

from scipy.stats import loguniform

from sklearn.model_selection import RandomizedSearchCV

param_distributions = {
    "alpha": loguniform(1e0, 1e3),
    "kernel__length_scale": loguniform(1e-2, 1e2),
    "kernel__periodicity": loguniform(1e0, 1e1),
}
kernel_ridge_tuned = RandomizedSearchCV(
    kernel_ridge,
    param_distributions=param_distributions,
    n_iter=500,
    random_state=0,
)
start_time = time.time()
kernel_ridge_tuned.fit(training_data, training_noisy_target)
print(f"Time for KernelRidge fitting: {time.time() - start_time:.3f} seconds")

Time for KernelRidge fitting: 3.112 seconds

现在拟合模型的计算成本更高，因为我们必须尝试几种超参数的组合。我们可以看看发现的超参数，以获得一些直觉。

kernel_ridge_tuned.best_params_

{'alpha': np.float64(1.991584977345022), 'kernel__length_scale': np.float64(0.7986499491396734), 'kernel__periodicity': np.float64(6.6072758064261095)}

查看最佳参数，我们会发现它们与默认值不同。我们还看到周期性更接近预期值： \(2 \pi\) .我们现在可以检查调整后的内核岭的预测。

start_time = time.time()
predictions_kr = kernel_ridge_tuned.predict(data)
print(f"Time for KernelRidge predict: {time.time() - start_time:.3f} seconds")

Time for KernelRidge predict: 0.001 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using tuned hyperparameters"
)

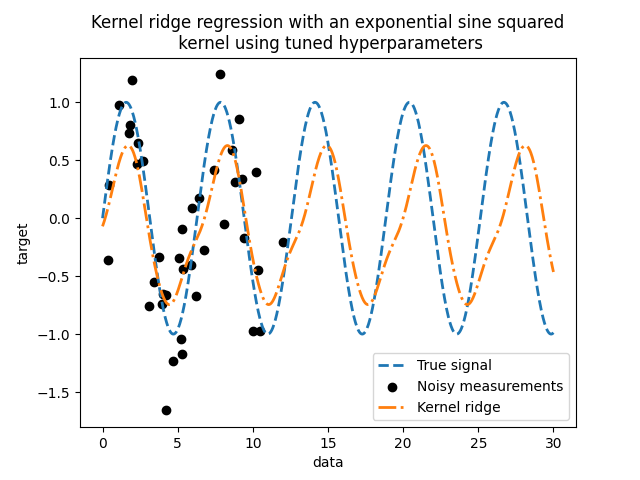
我们得到了一个更准确的模型。我们仍然观察到一些错误，主要是由于数据集中添加的噪音造成的。

高斯过程回归

现在，我们将使用 GaussianProcessRegressor 来拟合同一个数据集当训练高斯过程时，在拟合过程中优化内核的超参数。不需要外部超参数搜索。在这里，我们创建一个比内核岭回归器稍微复杂一些的内核：我们添加一个 WhiteKernel 用于估计数据集中的噪音。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) + WhiteKernel(
    1e-1
)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
start_time = time.time()
gaussian_process.fit(training_data, training_noisy_target)
print(
    f"Time for GaussianProcessRegressor fitting: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor fitting: 0.030 seconds

训练高斯过程的计算成本远低于使用随机搜索的核岭。我们可以检查我们计算的内核的参数。

gaussian_process.kernel_

0.675**2 * ExpSineSquared(length_scale=1.34, periodicity=6.57) + WhiteKernel(noise_level=0.182)

事实上，我们看到参数已经优化。看 periodicity 参数，我们发现我们发现一个接近理论值的周期 \(2 \pi\) .我们现在可以看看我们模型的预测。

start_time = time.time()
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)
print(
    f"Time for GaussianProcessRegressor predict: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor predict: 0.002 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Comparison between kernel ridge and gaussian process regressor")

我们观察到核岭和高斯过程回归量的结果很接近。然而，高斯过程回归量还提供了核岭无法提供的不确定性信息。由于目标函数的概率公式，高斯过程可以输出标准差（或协方差）以及目标函数的平均预测。

然而，这是有代价的：使用高斯过程计算预测的时间更长。

最终结论

我们可以就这两个模型推断的可能性给出最后的结论。事实上，我们只提供了信号的开始作为训练集。使用周期性核迫使我们的模型重复训练集中发现的模式。使用该核心信息以及两个模型的外推能力，我们观察到模型将继续预测sin模式。

高斯过程允许将核组合在一起。因此，我们可以将指数sin平方核与辐射基函数核联系在一起。

from sklearn.gaussian_process.kernels import RBF

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) * RBF(
    length_scale=15, length_scale_bounds="fixed"
) + WhiteKernel(1e-1)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
gaussian_process.fit(training_data, training_noisy_target)
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Effect of using a radial basis function kernel")

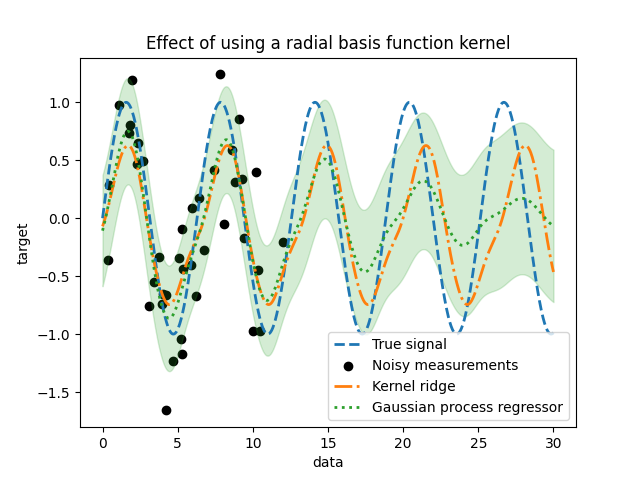
一旦在训练中没有样本可用，使用径向基函数核的效果将减弱周期性效应。随着测试样本与训练样本的距离越来越远，预测结果会向其平均值收敛，标准差也会增加。

相关实例

高斯过程回归：基本入门示例

Gaussian Processes regression: basic introductory example

HuberRegressor与Ridge在具有强异常值的数据集上

HuberRegressor vs Ridge on dataset with strong outliers

普通最小二乘和岭回归

Ordinary Least Squares and Ridge Regression

绘制岭系数作为正规化的函数

Plot Ridge coefficients as a function of the regularization