备注
Go to the end 下载完整的示例代码。或者通过浏览器中的MysterLite或Binder运行此示例
Lasso型号选择:AIC-BIC /交叉验证#
此示例重点关注Lasso模型的模型选择,Lasso模型是线性模型,回归问题具有L1罚分。
事实上,可以使用多种策略来选择正规化参数的值:通过交叉验证或使用信息标准,即AIC或BIC。
接下来,我们将详细讨论不同的策略。
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
数据集#
在本例中,我们将使用糖尿病数据集。
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
X.head()
此外,我们在原始数据中添加了一些随机特征,以更好地说明Lasso模型执行的特征选择。
import numpy as np
import pandas as pd
rng = np.random.RandomState(42)
n_random_features = 14
X_random = pd.DataFrame(
rng.randn(X.shape[0], n_random_features),
columns=[f"random_{i:02d}" for i in range(n_random_features)],
)
X = pd.concat([X, X_random], axis=1)
# Show only a subset of the columns
X[X.columns[::3]].head()
通过信息标准选择Lasso#
LassoLarsIC 提供了Lasso估计器,该估计器使用Akaike信息准则(AIC)或Bayes信息准则(BIC)来选择正规化参数Alpha的最佳值。
在匹配模型之前,我们将使用 StandardScaler .此外,我们将测量适应和调整超参数Alpha的时间,以便与交叉验证策略进行比较。
我们将首先用AIC准则拟合Lasso模型。
import time
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
start_time = time.time()
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
fit_time = time.time() - start_time
我们存储期间使用的每个Alpha值的AIC指标 fit .
results = pd.DataFrame(
{
"alphas": lasso_lars_ic[-1].alphas_,
"AIC criterion": lasso_lars_ic[-1].criterion_,
}
).set_index("alphas")
alpha_aic = lasso_lars_ic[-1].alpha_
现在,我们使用BIC准则执行相同的分析。
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
results["BIC criterion"] = lasso_lars_ic[-1].criterion_
alpha_bic = lasso_lars_ic[-1].alpha_
我们可以检查 alpha 导致最小AIC和BIC。
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results.style.apply(highlight_min)
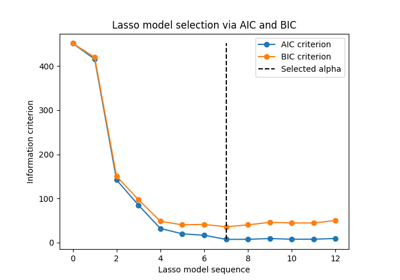
最后,我们可以绘制不同Alpha值的AIC和BIC值。图中的垂直线对应于为每个标准选择的Alpha。选择的Alpha对应于AIC或BIC标准的最小值。
ax = results.plot()
ax.vlines(
alpha_aic,
results["AIC criterion"].min(),
results["AIC criterion"].max(),
label="alpha: AIC estimate",
linestyles="--",
color="tab:blue",
)
ax.vlines(
alpha_bic,
results["BIC criterion"].min(),
results["BIC criterion"].max(),
label="alpha: BIC estimate",
linestyle="--",
color="tab:orange",
)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel("criterion")
ax.set_xscale("log")
ax.legend()
_ = ax.set_title(
f"Information-criterion for model selection (training time {fit_time:.2f}s)"
)
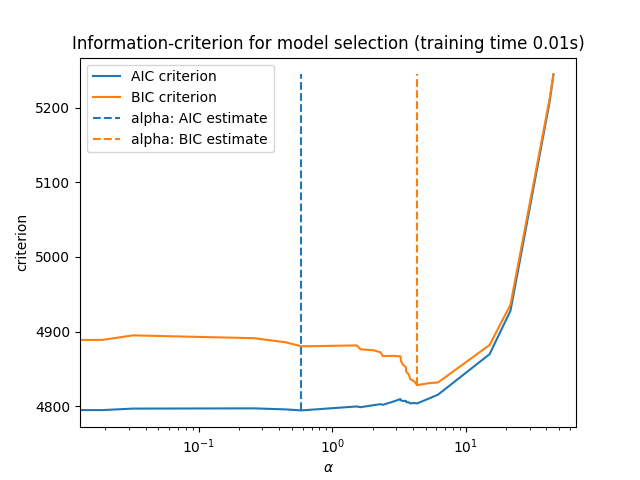
用信息准则进行模型选择是非常快的。它依赖于计算提供给 fit .这两个标准都根据训练集误差估计模型概括误差,并惩罚这种过于乐观的误差。然而,这种惩罚依赖于对自由度和噪音方差的正确估计。两者都是针对大样本(渐进结果)推导的,并假设模型是正确的,即数据实际上是由该模型生成的。
当问题条件恶劣(特征多于样本)时,这些模型也往往会崩溃。然后需要提供噪音方差的估计。
通过交叉验证选择Lasso#
Lasso估计器可以使用不同的求解器来实现:坐标下降和最小角度回归。它们在执行速度和数字错误来源方面有所不同。
在scikit-learn中,有两种不同的估计器可用于集成交叉验证: LassoCV 和 LassoLarsCV 分别用坐标下降法和最小角回归法求解。
在本节的其余部分,我们将介绍这两种方法。对于这两种算法,我们将使用20倍交叉验证策略。
通过坐标下降的套索#
让我们首先使用 LassoCV .
from sklearn.linear_model import LassoCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
import matplotlib.pyplot as plt
ymin, ymax = 2300, 3800
lasso = model[-1]
plt.semilogx(lasso.alphas_, lasso.mse_path_, linestyle=":")
plt.plot(
lasso.alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha: CV estimate")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(
f"Mean square error on each fold: coordinate descent (train time: {fit_time:.2f}s)"
)

Lasso通过最小角度回归#
让我们首先使用 LassoLarsCV .
from sklearn.linear_model import LassoLarsCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoLarsCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
lasso = model[-1]
plt.semilogx(lasso.cv_alphas_, lasso.mse_path_, ":")
plt.semilogx(
lasso.cv_alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha CV")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(f"Mean square error on each fold: Lars (train time: {fit_time:.2f}s)")
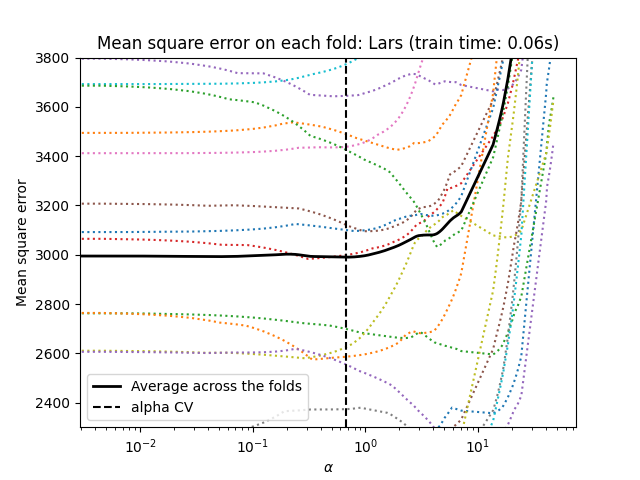
交叉验证方法总结#
两种算法给出的结果大致相同。
Lars仅为路径中的每个扭结计算解决方案路径。因此,当只有很少的扭结时,这种方法非常有效,如果特征或样本很少,就是这种情况。此外,它能够在不设置任何超参数的情况下计算完整路径。相反,坐标下降计算预先指定的网格上的路径点(这里我们使用默认值)。因此,如果网格点的数量小于路径中扭结的数量,则效率更高。如果特征的数量确实很大并且在每个交叉验证文件中都有足够的样本可供选择,那么这种策略可能会很有趣。在数字误差方面,对于高度相关的变量,Lars会积累更多误差,而坐标下降算法只会对网格上的路径进行采样。
请注意阿尔法的最佳值在每个折叠中如何变化。这说明了为什么当尝试评估通过交叉验证选择参数的方法的性能时,嵌套交叉验证是一种很好的策略:这种参数选择可能不是仅对未见测试集进行最终评估的最佳选择。
结论#
在本教程中,我们介绍了两种选择最佳超参数的方法 alpha :一种策略找到的最佳价值 alpha 通过仅使用训练集和一些信息标准,另一种策略基于交叉验证。
在这个例子中,两种方法的工作原理相似。样本内超参数选择甚至显示了其在计算性能方面的功效。然而,只有当样本数量与特征数量相比足够大时才能使用它。
这就是为什么通过交叉验证进行超参数优化是一种安全策略:它适用于不同的设置。
Total running time of the script: (0分0.738秒)
相关实例
Gallery generated by Sphinx-Gallery <https://sphinx-gallery.github.io> _