备注
Go to the end 下载完整的示例代码。或者通过浏览器中的MysterLite或Binder运行此示例
线性模型系数解释中的常见陷阱#
在线性模型中，目标值被建模为要素的线性组合（请参阅 线性模型 用户指南部分，描述scikit-learn中提供的一组线性模型）。多个线性模型中的系数代表给定特征， \(X_i\) 而目标， \(y\) 假设所有其他特征保持不变 (conditional dependence ).这与密谋不同 \(X_i\) 与 \(y\) 并适应线性关系：在这种情况下，在估计中考虑其他特征的所有可能值（边际依赖性）。
这个例子将为解释线性模型中的系数提供一些提示，指出当线性模型不适合描述数据集或特征相关时出现的问题。
备注
请记住，功能 \(X\) 和结果 \(y\) 通常是我们未知的数据生成过程的结果。机器学习模型经过训练以逼近未观察到的数学函数， \(X\) 到 \(y\) 来自样本数据。因此，对模型做出的任何解释都不一定能推广到真正的数据生成过程。当模型质量较差或样本数据不代表总体时，尤其如此。
我们将使用来自 "Current Population Survey" 从1985年开始，根据经验、年龄或教育程度等各种特征来预测工资。
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
数据集：工资#
我们从 OpenML .请注意，设置参数 as_frame To True将以熊猫rame的形式检索数据。
from sklearn.datasets import fetch_openml
survey = fetch_openml(data_id=534, as_frame=True)
然后，我们识别特征 X 和指标 y ：工资列是我们的目标变量（即，我们想要预测的变量）。
X = survey.data[survey.feature_names]
X.describe(include="all")
请注意，数据集包含分类变量和数值变量。我们在对数据集进行预处理时需要考虑到这一点。
X.head()
我们的预测目标：工资。工资被描述为以每小时美元为单位的浮点数。
y = survey.target.values.ravel()
survey.target.head()
0 5.10
1 4.95
2 6.67
3 4.00
4 7.50
Name: WAGE, dtype: float64
我们将样本分成一个序列和一个测试数据集。以下探索性分析中将仅使用火车数据集。这是一种模拟对未知目标执行预测的真实情况的方法，我们不希望我们的分析和决策受到我们对测试数据的了解的偏差。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
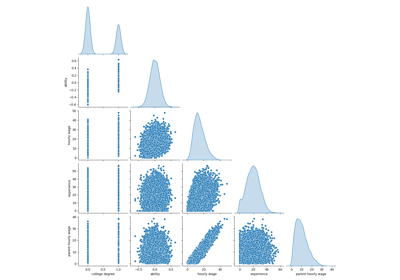
首先，让我们通过观察变量分布及其之间的成对关系来获得一些见解。将仅使用数字变量。在下面的图中，每个点代表一个样本。
train_dataset = X_train.copy()
train_dataset.insert(0, "WAGE", y_train)
_ = sns.pairplot(train_dataset, kind="reg", diag_kind="kde")
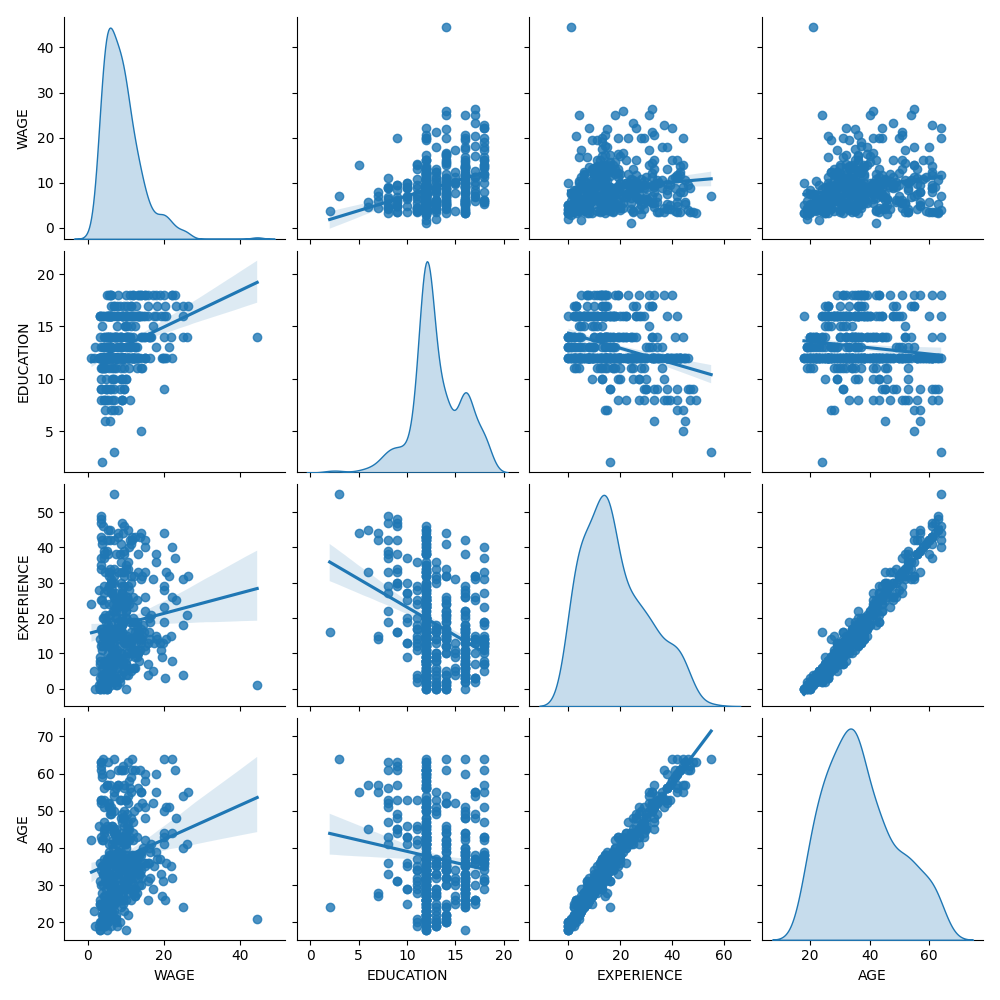
仔细观察工资分布会发现它有一条长尾。出于这个原因，我们应该取其对数，将其大约转化为正态分布（线性模型，例如山脊或套索最适合误差的正态分布）。
当教育增加时，工资也增加。请注意，这里表示的工资和教育之间的依赖关系是边际依赖关系，即它描述特定变量的行为，而不保持其他变量固定。
此外，经验和年龄呈强线性相关。
机器学习管道#
为了设计我们的机器学习管道，我们首先手动检查我们正在处理的数据类型：
survey.data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 534 entries, 0 to 533
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 EDUCATION 534 non-null int64
1 SOUTH 534 non-null category
2 SEX 534 non-null category
3 EXPERIENCE 534 non-null int64
4 UNION 534 non-null category
5 AGE 534 non-null int64
6 RACE 534 non-null category
7 OCCUPATION 534 non-null category
8 SECTOR 534 non-null category
9 MARR 534 non-null category
dtypes: category(7), int64(3)
memory usage: 17.3 KB
如前所述，数据集包含不同数据类型的列，我们需要对每个数据类型应用特定的预处理。特别是，如果分类变量不首先编码为整数，则无法包含在线性模型中。此外，为了避免类别特征被视为有序值，我们需要对它们进行一热编码。我们的预处理器将
一热编码（即，按类别生成列）类别列，仅适用于非二元类别变量;
作为第一种方法（我们将在数值的正常化将如何影响我们的讨论之后看到），保持数值原样。
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import OneHotEncoder
categorical_columns = ["RACE", "OCCUPATION", "SECTOR", "MARR", "UNION", "SEX", "SOUTH"]
numerical_columns = ["EDUCATION", "EXPERIENCE", "AGE"]
preprocessor = make_column_transformer(
(OneHotEncoder(drop="if_binary"), categorical_columns),
remainder="passthrough",
verbose_feature_names_out=False, # avoid to prepend the preprocessor names
)
为了将数据集描述为线性模型，我们使用具有非常小规则化的岭回归器，并对工资的log进行建模。
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
),
)
处理数据集#
首先，我们适应模型。
model.fit(X_train, y_train)
然后，我们检查计算模型的性能，在测试集上绘制其预测并计算模型的中位数绝对误差。
from sklearn.metrics import PredictionErrorDisplay, median_absolute_error
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
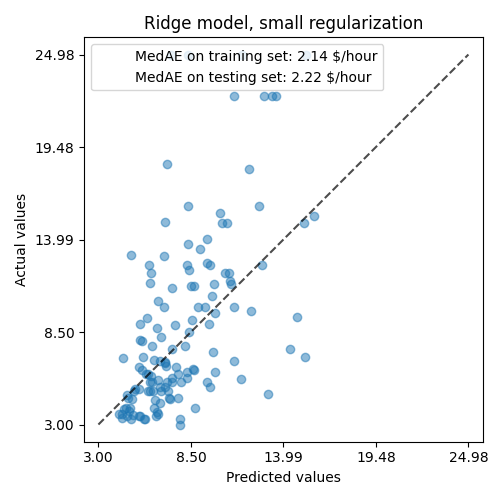
所学到的模型远非一个能够做出准确预测的好模型：当查看上面的图表时，这一点很明显，其中好的预测应该位于黑色虚线上。
在下面的部分中，我们将解释模型的系数。当我们这样做时，我们应该记住，我们得出的任何结论都是关于我们构建的模型，而不是关于数据的真实（真实世界）生成过程。
解释系数：规模很重要#
首先，我们可以看看我们所匹配的回归量的系数值。
feature_names = model[:-1].get_feature_names_out()
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients"],
index=feature_names,
)
coefs
年龄系数以“每活年的美元/小时”表示，而教育系数则以“每受教育年的美元/小时”表示。系数的这种表示有助于明确模型的实际预测：增加 \(1\) 年龄意味着年龄的减少 \(0.030867\) 美元/小时，而增加 \(1\) 教育一年意味着 \(0.054699\) 美元/小时。另一方面，分类变量（如UNION或SEX）是多维数，取值为0或1。其系数以美元/小时表示。然后，我们不能比较不同系数的大小，因为特征具有不同的自然尺度，因此值范围也不同，因为它们的测量单位不同。如果我们绘制系数，这将更加明显。
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.xlabel("Raw coefficient values")
plt.subplots_adjust(left=0.3)
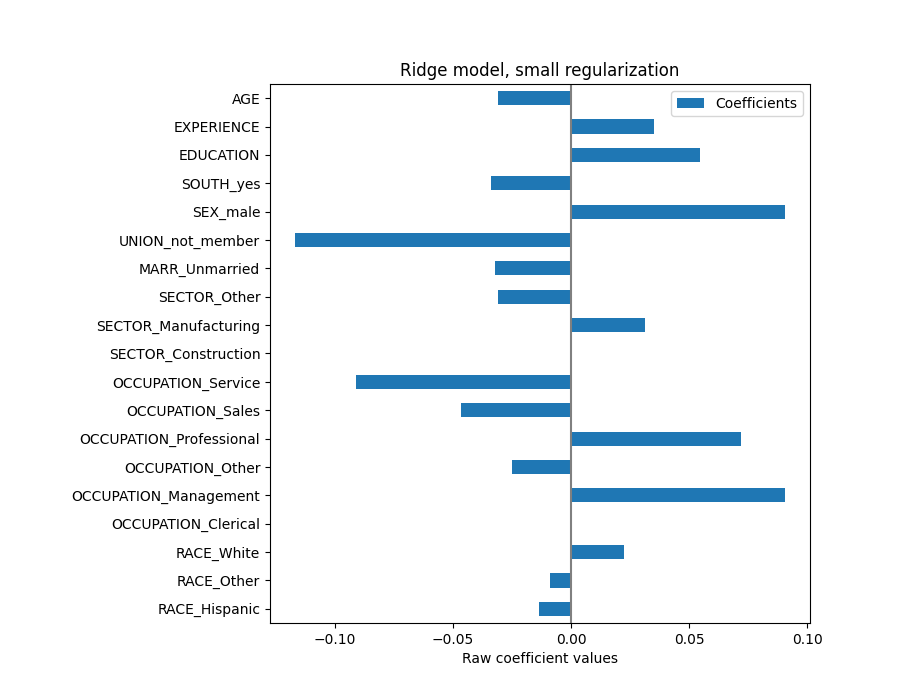
事实上，从上面的图表来看，决定工资的最重要因素似乎是变量UNION，即使我们的直觉可能告诉我们，经验等变量应该产生更大的影响。
查看系数图来衡量特征重要性可能会产生误导，因为其中一些特征的变化范围很小，而其他特征，如年龄，变化更大，几十年。
如果我们比较不同特征的标准差，这是显而易见的。
X_train_preprocessed = pd.DataFrame(
model[:-1].transform(X_train), columns=feature_names
)
X_train_preprocessed.std(axis=0).plot.barh(figsize=(9, 7))
plt.title("Feature ranges")
plt.xlabel("Std. dev. of feature values")
plt.subplots_adjust(left=0.3)
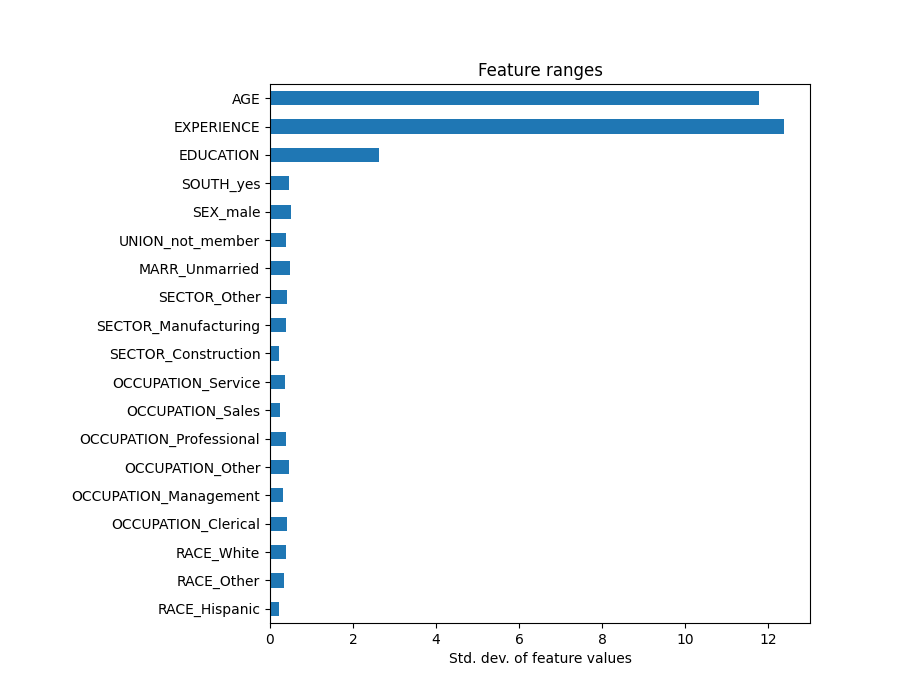
Multiplying the coefficients by the standard deviation of the related feature would reduce all the coefficients to the same unit of measure. As we will see after this is equivalent to normalize numerical variables to their standard deviation, as \(y = \sum{coef_i \times X_i} = \sum{(coef_i \times std_i) \times (X_i / std_i)}\).
通过这种方式，我们强调，特征的方差越大，输出中相应系数的权重就越大，所有其他条件都相同。
coefs = pd.DataFrame(
model[-1].regressor_.coef_ * X_train_preprocessed.std(axis=0),
columns=["Coefficient importance"],
index=feature_names,
)
coefs.plot(kind="barh", figsize=(9, 7))
plt.xlabel("Coefficient values corrected by the feature's std. dev.")
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
既然系数已经缩放，我们就可以安全地比较它们了。
警告
为什么上面的图表表明年龄的增加会导致工资的减少？为什么 initial pairplot 正在告诉相反的事情吗？
上面的图告诉我们当所有其他特征保持不变时，特定特征和目标之间的依赖关系，即 conditional dependencies .当所有其他特征保持不变时，年龄的增加将导致工资的减少。相反，当所有其他特征保持不变时，经验的增加将导致工资的增加。此外，年龄、经验和教育是对模型影响最大的三个变量。
解释系数：谨慎对待因果关系#
线性模型是衡量统计关联的好工具，但我们在做出因果关系声明时应该谨慎，毕竟相关性并不总是意味着因果关系。这在社会科学中尤其困难，因为我们观察到的变量只能充当潜在因果过程的代理。
在我们的特定案例中，我们可以将个人的教育视为其专业能力的代表，这是我们感兴趣但无法观察的真正变量。我们当然愿意认为，在学校呆得更长时间会提高技术能力，但因果关系也很可能相反。也就是说，那些技术能力强的人往往会在学校呆得更长。
雇主不太可能关心是哪种情况（或者是两者兼而有之），只要他们仍然相信受过更多教育的人更适合这份工作，他们就会很乐意支付更高的工资。
当考虑某种形式的干预措施（例如政府对大学学位的补贴或鼓励个人接受高等教育的宣传材料）时，这种影响的混淆就会成为问题。这些措施的有效性最终可能会被夸大，特别是如果混淆程度很强的话。我们的模型预测 \(0.054699\) 每一年教育的小时工资增加。由于这种混杂，实际因果效应可能较低。
检查系数的变异性#
我们可以通过交叉验证检查系数变异性：这是数据扰动的一种形式（与 resampling ).
如果系数在改变输入数据集时变化很大，则不能保证其鲁棒性，并且可能应谨慎解释。
from sklearn.model_selection import RepeatedKFold, cross_validate
cv = RepeatedKFold(n_splits=5, n_repeats=5, random_state=0)
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[
est[-1].regressor_.coef_ * est[:-1].transform(X.iloc[train_idx]).std(axis=0)
for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
],
columns=feature_names,
)
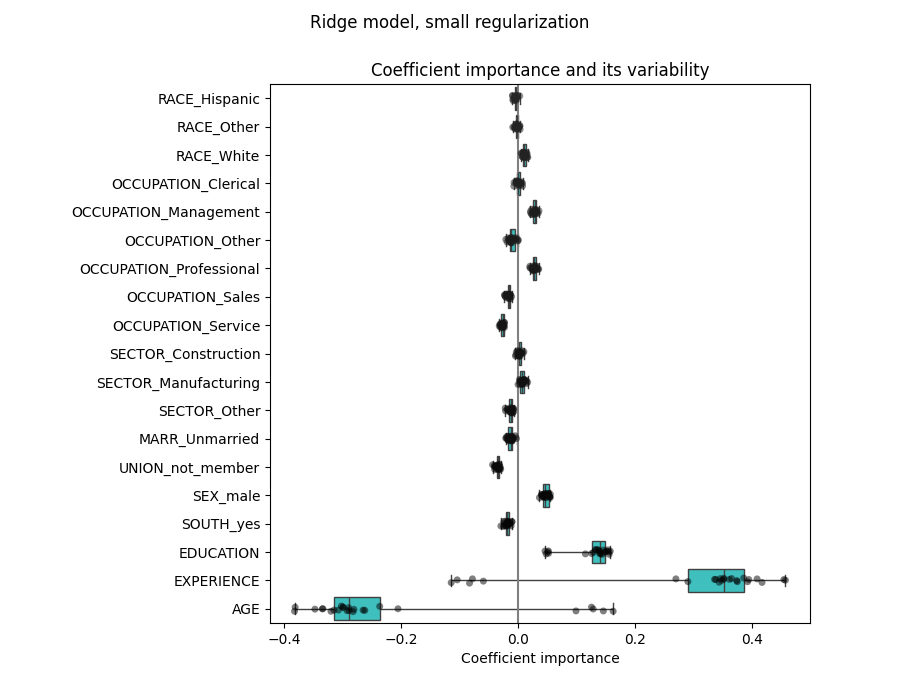
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.xlabel("Coefficient importance")
plt.title("Coefficient importance and its variability")
plt.suptitle("Ridge model, small regularization")
plt.subplots_adjust(left=0.3)
相关变量的问题#
年龄和经验系数受到强变异性的影响，这可能是由于2个特征之间的共线性造成的：由于数据中年龄和经验一起变化，因此它们的影响很难区分。
为了验证这一解释，我们绘制了年龄和经验系数的变异性。
plt.ylabel("Age coefficient")
plt.xlabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")
有两个地区：当经验系数为正值时，年龄系数为负值，反之亦然。
为了更进一步，我们删除了2个功能之一，并检查对模型稳定性的影响。
column_to_drop = ["AGE"]
cv_model = cross_validate(
model,
X.drop(columns=column_to_drop),
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[
est[-1].regressor_.coef_
* est[:-1].transform(X.drop(columns=column_to_drop).iloc[train_idx]).std(axis=0)
for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
],
columns=feature_names[:-1],
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5)
plt.axvline(x=0, color=".5")
plt.title("Coefficient importance and its variability")
plt.xlabel("Coefficient importance")
plt.suptitle("Ridge model, small regularization, AGE dropped")
plt.subplots_adjust(left=0.3)
EXPERIENCE系数的估计值现在显示变异性大大降低。经验对于在交叉验证期间训练的所有模型仍然很重要。
预处理数字变量#
如上所述（请参阅“：ref：' the-pipeline '”），我们还可以选择在训练模型之前缩放数值。当我们对山脊中的所有它们应用类似量的正规化时，这可能很有用。重新定义预处理器，以便将均值和标度变量减去单位方差。
from sklearn.preprocessing import StandardScaler
preprocessor = make_column_transformer(
(OneHotEncoder(drop="if_binary"), categorical_columns),
(StandardScaler(), numerical_columns),
)
该模型将保持不变。
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
),
)
model.fit(X_train, y_train)
同样，我们使用模型的绝对误差中位数和R平方系数检查计算模型的性能。
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
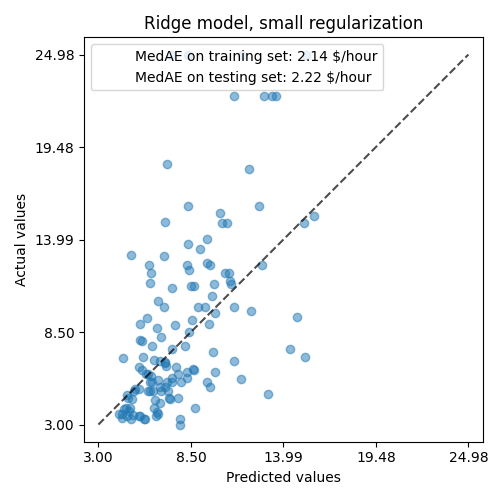
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
对于系数分析，这次不需要缩放，因为它是在预处理步骤期间执行的。
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
现在我们检查几个交叉验证折叠中的系数。与上面的例子一样，我们不需要通过std来缩放系数。dev.由于此缩放已经在管道的预处理步骤中完成了。
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)
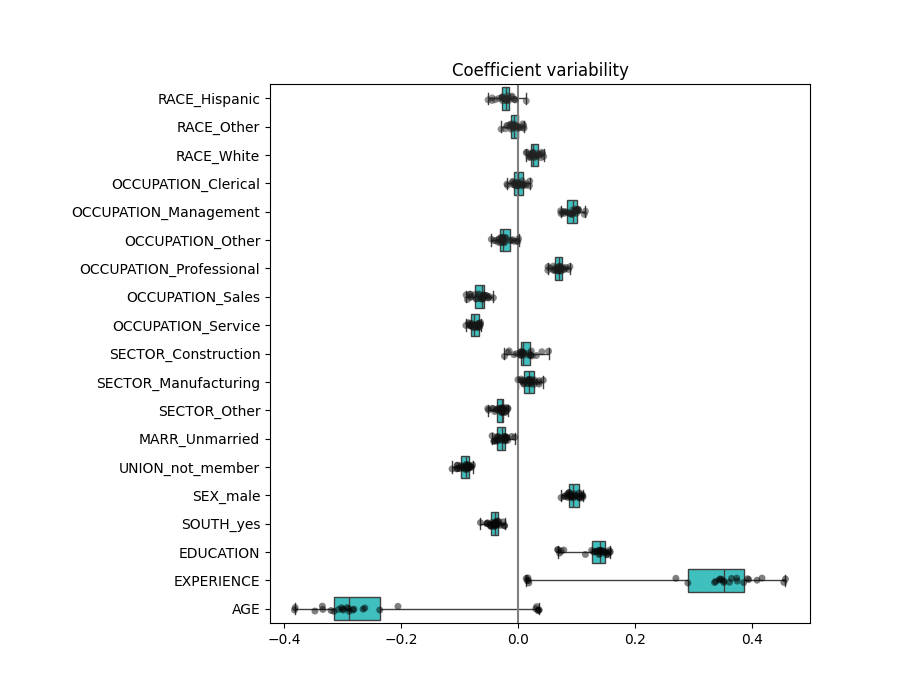
结果与非正规化情况非常相似。
正则化线性模型#
在机器学习实践中，岭回归更常与不可忽视的正规化一起使用。
上面，我们将这种正规化限制在非常小的量。正规化改进了问题的条件条件并减少了估计的方差。 RidgeCV 应用交叉验证以确定正规化参数的哪个值 (alpha ）最适合预测。
from sklearn.linear_model import RidgeCV
alphas = np.logspace(-10, 10, 21) # alpha values to be chosen from by cross-validation
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=RidgeCV(alphas=alphas),
func=np.log10,
inverse_func=sp.special.exp10,
),
)
model.fit(X_train, y_train)
首先我们检查 \(\alpha\) 已被选中。
model[-1].regressor_.alpha_
np.float64(10.0)
然后我们检查预测的质量。
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, optimum regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
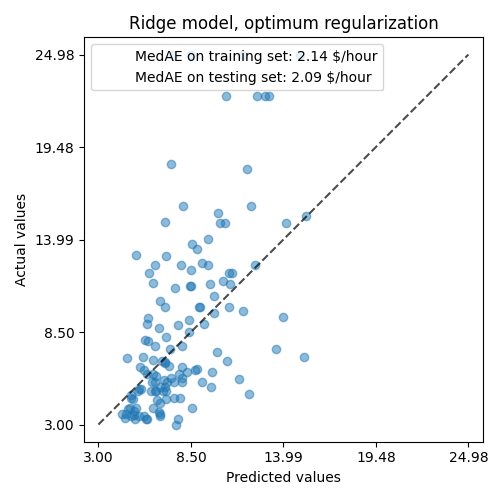
规则化模型的数据再现能力与非规则化模型的数据相似。
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, with regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
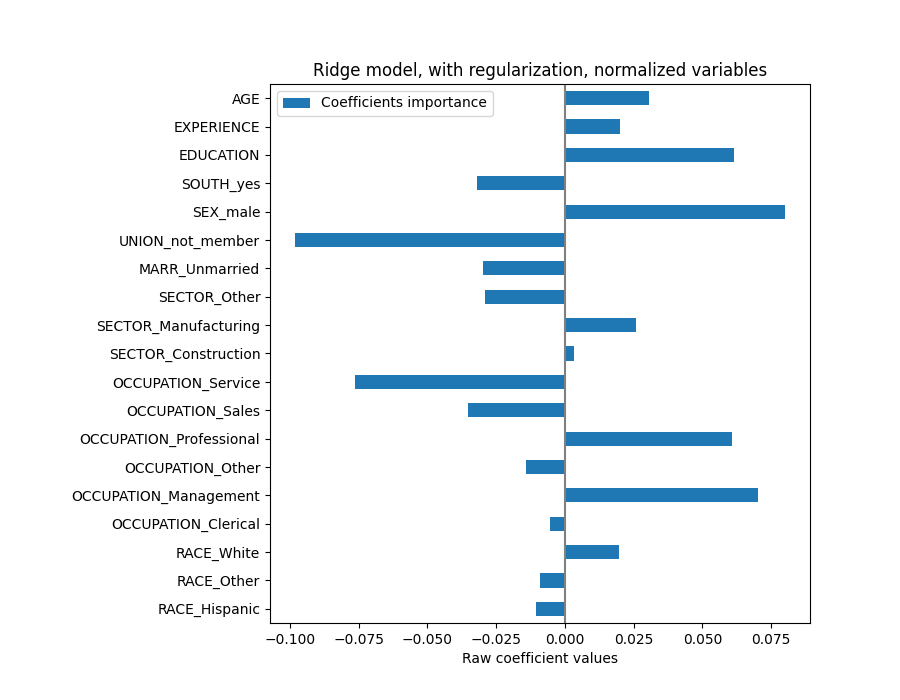
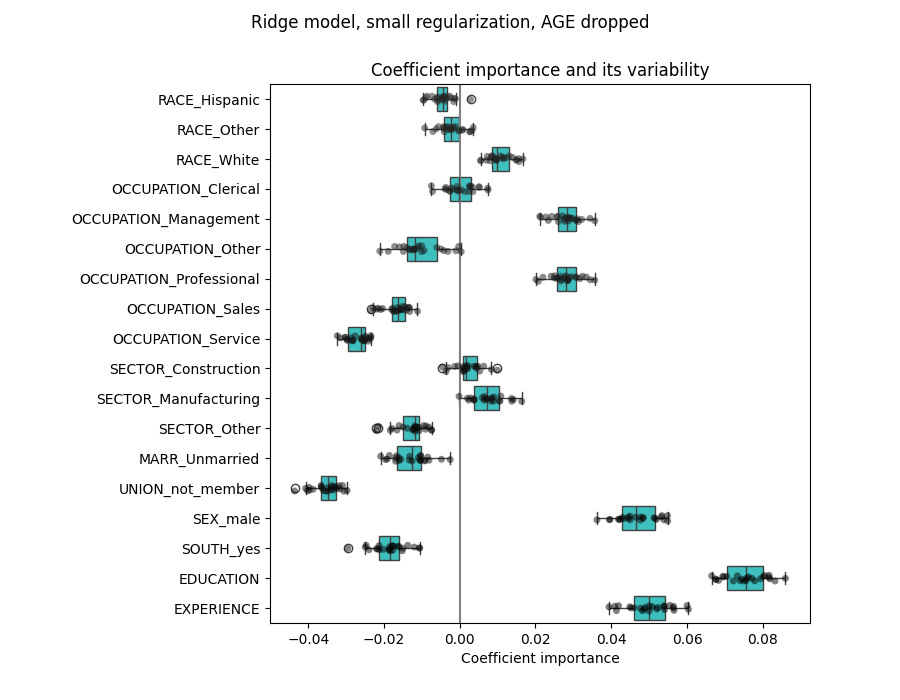
系数显着不同。年龄和经验系数都为正值，但现在它们对预测的影响较小。
正规化减少了相关变量对模型的影响，因为权重在两个预测变量之间共享，因此两个预测变量都不会单独具有很强的权重。
另一方面，通过正规化获得的权重更加稳定（请参阅 岭回归与分类 用户指南部分）。在交叉验证中，从数据扰动获得的图中可以看到这种增加的稳定性。这个情节可以与 previous one .
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
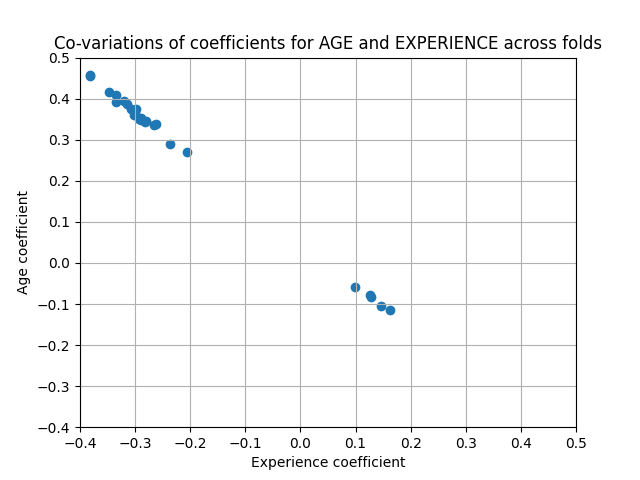
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.ylabel("Age coefficient")
plt.xlabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")
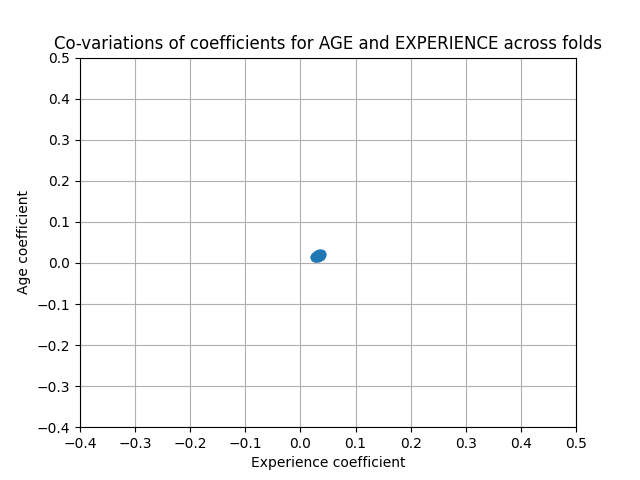
稀疏系数线性模型#
考虑数据集中相关变量的另一种可能性是估计稀疏系数。在某种程度上，当我们在之前的岭估计中删除AGE列时，我们已经手动完成了这一操作。
套索模型（请参阅 Lasso 用户指南部分）估计稀疏系数。 LassoCV 应用交叉验证以确定正规化参数的哪个值 (alpha ）最适合于模型估计。
from sklearn.linear_model import LassoCV
alphas = np.logspace(-10, 10, 21) # alpha values to be chosen from by cross-validation
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=LassoCV(alphas=alphas, max_iter=100_000),
func=np.log10,
inverse_func=sp.special.exp10,
),
)
_ = model.fit(X_train, y_train)
首先我们验证哪个值 \(\alpha\) 已被选中。
model[-1].regressor_.alpha_
np.float64(0.001)
然后我们检查预测的质量。
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(6, 6))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Lasso model, optimum regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
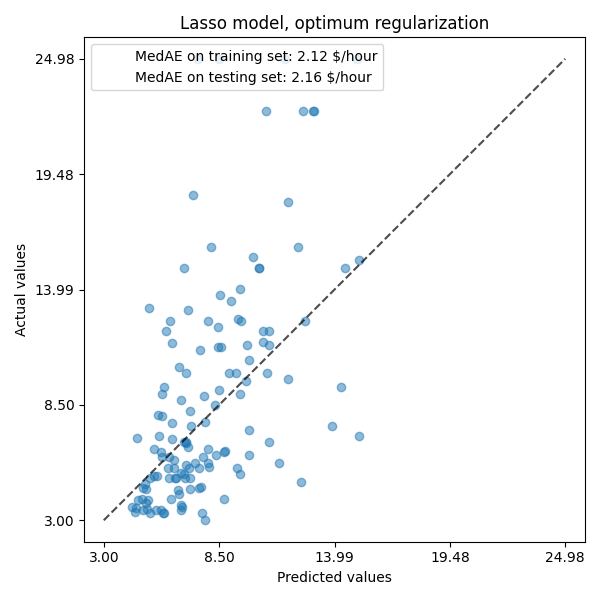
对于我们的数据集来说，该模型的预测性也不是很强。
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot(kind="barh", figsize=(9, 7))
plt.title("Lasso model, optimum regularization, normalized variables")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
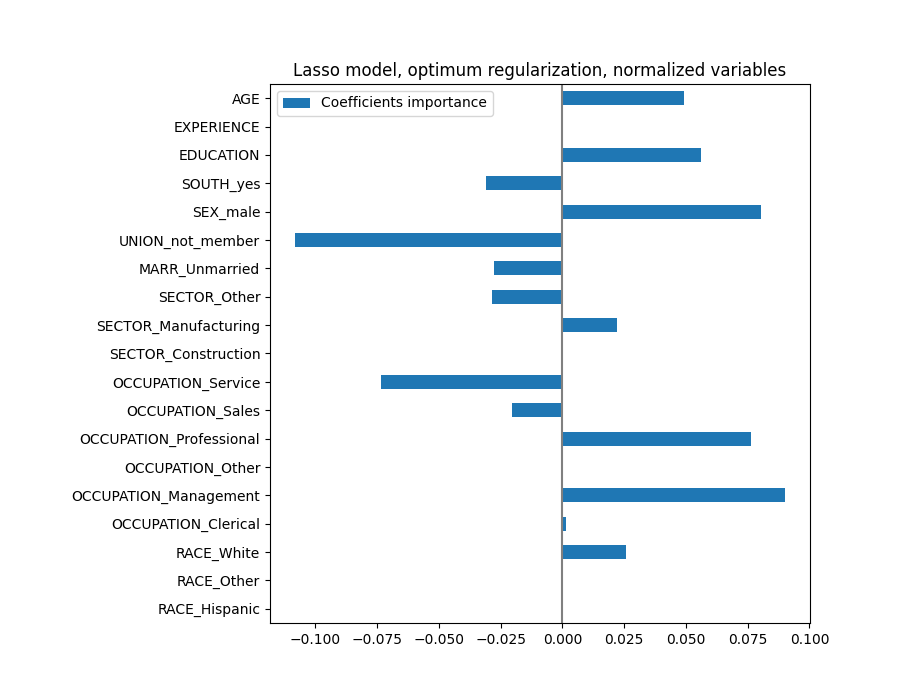
Lasso模型识别年龄和经验之间的相关性，并为了预测而抑制其中之一。
重要的是要记住，已删除的系数可能仍然与结果本身相关：模型选择抑制它们，因为它们除了其他特征之外几乎没有或没有带来额外的信息。此外，这种选择对于相关特征来说是不稳定的，并且应谨慎解释。
事实上，我们可以检查跨折叠系数的变异性。
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=100)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)
我们观察到年龄和经验系数因折叠而变化很大。
错误的因果解释#
政策制定者可能想知道教育对工资的影响，以评估旨在吸引人们接受更多教育的某些政策是否具有经济意义。虽然机器学习模型非常适合测量统计关联，但它们通常无法推断因果影响。
我们可能很容易从上一个模型（或任何相关模型）中查看教育与工资的系数，并得出结论，它捕捉了标准化教育变量变化对工资的真正影响。
不幸的是，可能存在未观察到的混杂变量，它们要么夸大了该系数，要么缩小了该系数。混杂变量是导致教育和工资的变量。这种变量的一个例子是能力。据推测，能力更强的人更有可能接受教育，同时更有可能在任何教育水平上获得更高的时薪。在这种情况下，能力诱导积极的 Omitted Variable Bias (OVB)教育系数，从而夸大了教育对工资的影响。
看到 机器学习无法推断因果效应 对于OVB能力的模拟案例。
经验教训#
系数必须缩放到相同的测量单位才能检索特征重要性。用功能的标准偏差来扩展它们是一个有用的代理。
当存在混杂效应时，解释因果关系就很困难。如果两个变量之间的关系也受到未观察到的东西的影响，那么我们在做出因果关系的结论时就应该小心。
多元线性模型中的系数代表给定特征和目标之间的依赖性， conditional 关于其他功能。
相关的功能诱导的不稳定性系数的线性模型和它们的影响不能很好地取笑分开。
不同的线性模型对特征相关性的反应不同，并且系数可能彼此存在显着差异。
检查交叉验证循环折叠中的系数可以了解其稳定性。
系数不太可能具有任何因果意义。他们往往会受到未观察到的混杂因素的偏见。
检查工具可能不一定能提供有关真实数据生成过程的见解。
Total running time of the script: （0分14.056秒）
相关实例
Gallery generated by Sphinx-Gallery <https://sphinx-gallery.github.io> _