备注
Go to the end 下载完整的示例代码。或者通过浏览器中的MysterLite或Binder运行此示例
高斯过程回归:基本入门示例#
一个简单的一维回归示例,以两种不同的方式计算:
无噪音的案例
每个数据点已知噪音水平的有噪音情况
在这两种情况下,核参数都是使用最大似然原理估计的。
这些图以逐点95%置信区间的形式说明了高斯过程模型的插值属性及其概率性质。
注意 alpha 是控制假设训练点协方差矩阵上吉洪诺夫正规化强度的参数。
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
数据集生成#
我们将首先生成合成数据集。真正的生成过程被定义为 \(f(x) = x \sin(x)\) .
import numpy as np
X = np.linspace(start=0, stop=10, num=1_000).reshape(-1, 1)
y = np.squeeze(X * np.sin(X))
import matplotlib.pyplot as plt
plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("True generative process")
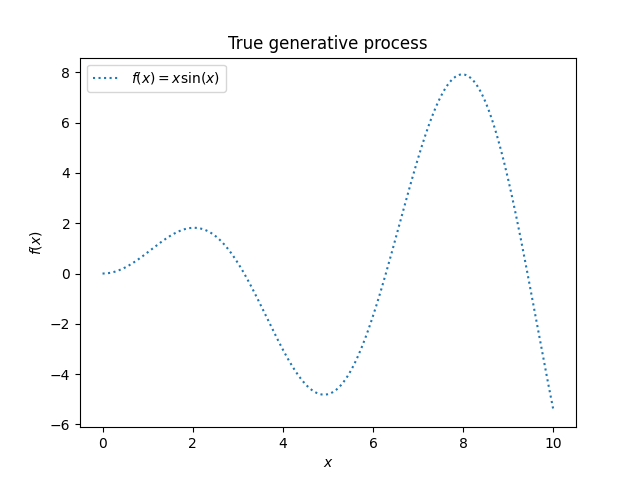
我们将在下一个实验中使用该数据集来说明高斯过程回归的工作原理。
无噪声目标示例#
在第一个例子中,我们将使用真正的生成过程,而不添加任何噪音。为了训练高斯过程回归,我们只选择少数样本。
rng = np.random.RandomState(1)
training_indices = rng.choice(np.arange(y.size), size=6, replace=False)
X_train, y_train = X[training_indices], y[training_indices]
现在,我们在这几个训练数据样本上拟合高斯过程。我们将使用径向基函数(RBF)内核和常数参数来拟合振幅。
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
kernel = 1 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e2))
gaussian_process = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
gaussian_process.fit(X_train, y_train)
gaussian_process.kernel_
5.02**2 * RBF(length_scale=1.43)
在匹配我们的模型后,我们看到内核的超参数已经被优化。现在,我们将使用内核计算完整数据集的平均预测并绘制95%置信区间。
mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)
plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.scatter(X_train, y_train, label="Observations")
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
X.ravel(),
mean_prediction - 1.96 * std_prediction,
mean_prediction + 1.96 * std_prediction,
alpha=0.5,
label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on noise-free dataset")
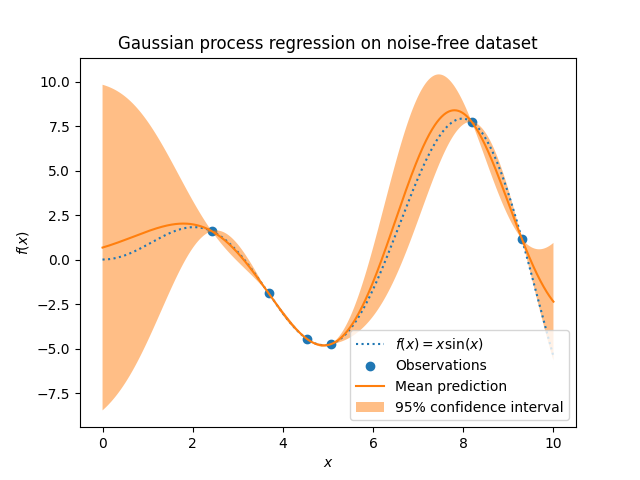
我们看到,对于在接近训练集中数据点的数据点上做出的预测,95%的置信度的幅度很小。每当样本远离训练数据时,我们的模型的预测就不太准确,模型预测也不太精确(不确定性更高)。
有噪音目标的示例#
这次我们可以重复类似的实验,向目标添加额外的噪音。它将允许查看噪音对装配模型的影响。
我们向目标添加一些具有任意标准差的随机高斯噪音。
noise_std = 0.75
y_train_noisy = y_train + rng.normal(loc=0.0, scale=noise_std, size=y_train.shape)
我们创建一个类似的高斯过程模型。除了内核之外,这次我们还指定参数 alpha 这可以解释为高斯噪音的方差。
gaussian_process = GaussianProcessRegressor(
kernel=kernel, alpha=noise_std**2, n_restarts_optimizer=9
)
gaussian_process.fit(X_train, y_train_noisy)
mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)
让我们像以前一样绘制平均预测和不确定性区域。
plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.errorbar(
X_train,
y_train_noisy,
noise_std,
linestyle="None",
color="tab:blue",
marker=".",
markersize=10,
label="Observations",
)
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
X.ravel(),
mean_prediction - 1.96 * std_prediction,
mean_prediction + 1.96 * std_prediction,
color="tab:orange",
alpha=0.5,
label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on a noisy dataset")
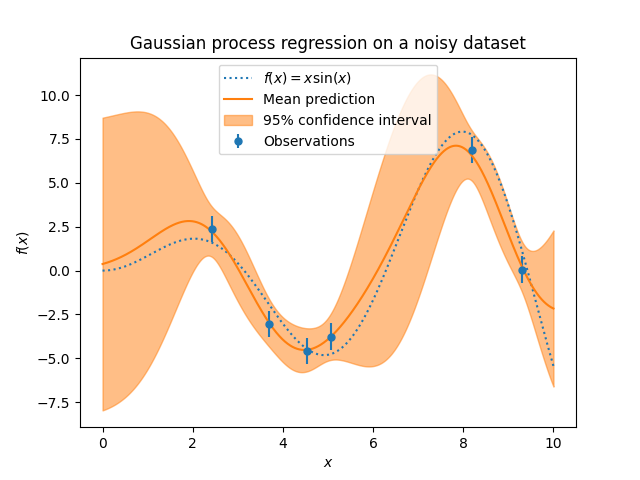
噪音会影响训练样本附近的预测:训练样本附近的预测不确定性更大,因为我们对给定级别的目标噪音进行了独立于输入变量的模型。
Total running time of the script: (0分0.492秒)
相关实例
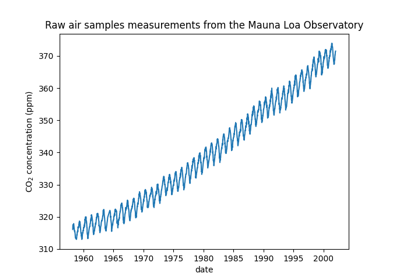
使用高斯过程回归(GPT)预测Mona Loa数据集的二氧化碳水平
Gallery generated by Sphinx-Gallery <https://sphinx-gallery.github.io> _