瑞士滚动和瑞士洞减少#

本笔记本旨在在经典Swiss Roll数据集上比较两种流行的非线性维度技术：T分布随机邻居嵌入（t-SNE）和局部线性嵌入（LLE）。然后，我们将探讨它们如何处理数据中增加的漏洞。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

瑞士卷#

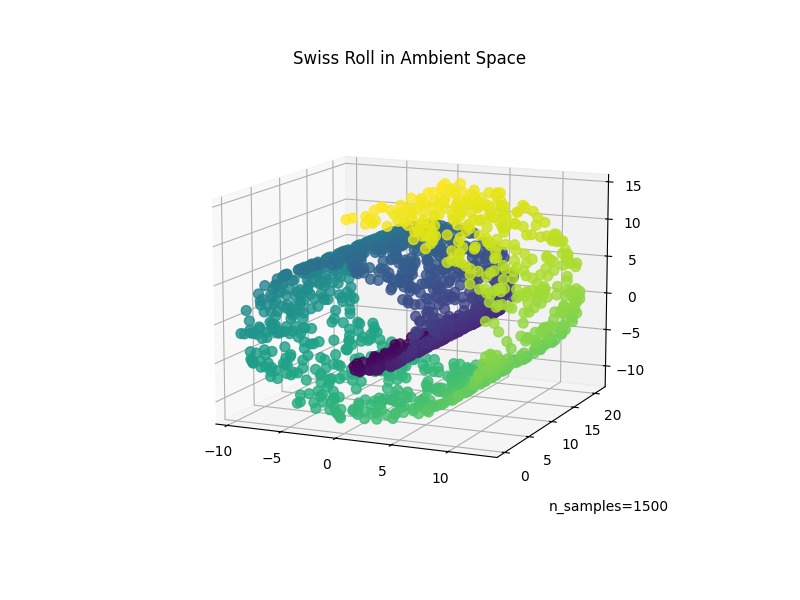
我们首先生成Swiss Roll数据集。

import matplotlib.pyplot as plt

from sklearn import datasets, manifold

sr_points, sr_color = datasets.make_swiss_roll(n_samples=1500, random_state=0)

现在，让我们看看我们的数据：

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sr_points[:, 0], sr_points[:, 1], sr_points[:, 2], c=sr_color, s=50, alpha=0.8
)
ax.set_title("Swiss Roll in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

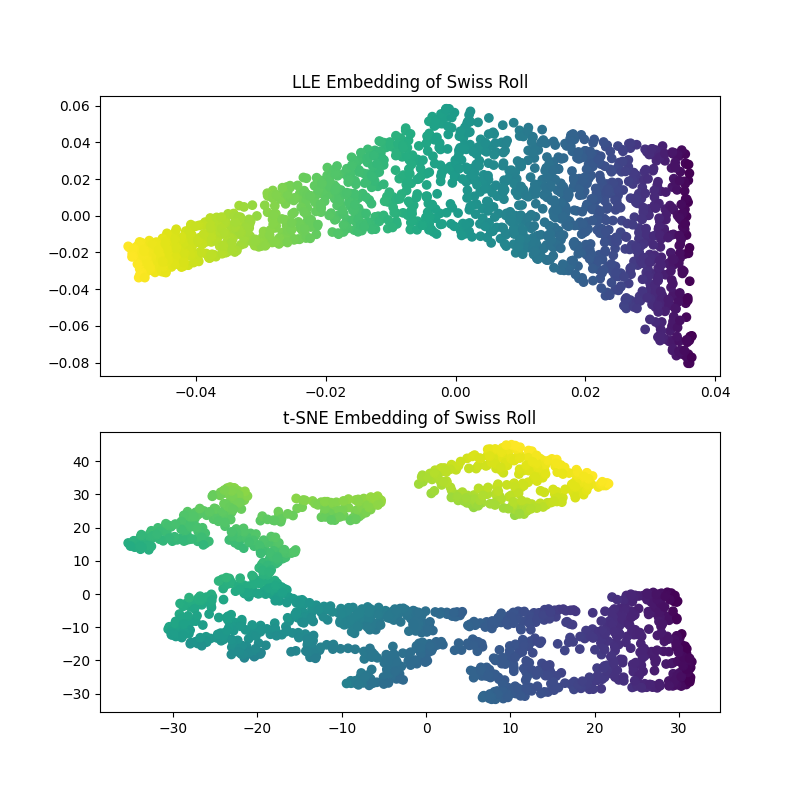
计算LLE和t-SNE嵌入后，我们发现LLE似乎非常有效地展开了Swiss Roll。另一方面，t-SNE能够保留数据的一般结构，但无法很好地代表原始数据的连续性。相反，它似乎不必要地将点的部分聚集在一起。

sr_lle, sr_err = manifold.locally_linear_embedding(
    sr_points, n_neighbors=12, n_components=2
)

sr_tsne = manifold.TSNE(n_components=2, perplexity=40, random_state=0).fit_transform(
    sr_points
)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sr_lle[:, 0], sr_lle[:, 1], c=sr_color)
axs[0].set_title("LLE Embedding of Swiss Roll")
axs[1].scatter(sr_tsne[:, 0], sr_tsne[:, 1], c=sr_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss Roll")

LLE Embedding of Swiss Roll, t-SNE Embedding of Swiss Roll

备注

LLE似乎正在从瑞士卷的中心（紫色）拉伸点。然而，我们观察到这只是数据生成方式的副产品。卷中心附近的点密度较高，这最终影响LLE如何在较低维度中重建数据。

瑞士洞#

现在让我们看看这两种算法如何处理我们给数据添加漏洞的情况。首先，我们生成Swiss-Hole数据集并绘制它：

sh_points, sh_color = datasets.make_swiss_roll(
    n_samples=1500, hole=True, random_state=0
)

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sh_points[:, 0], sh_points[:, 1], sh_points[:, 2], c=sh_color, s=50, alpha=0.8
)
ax.set_title("Swiss-Hole in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

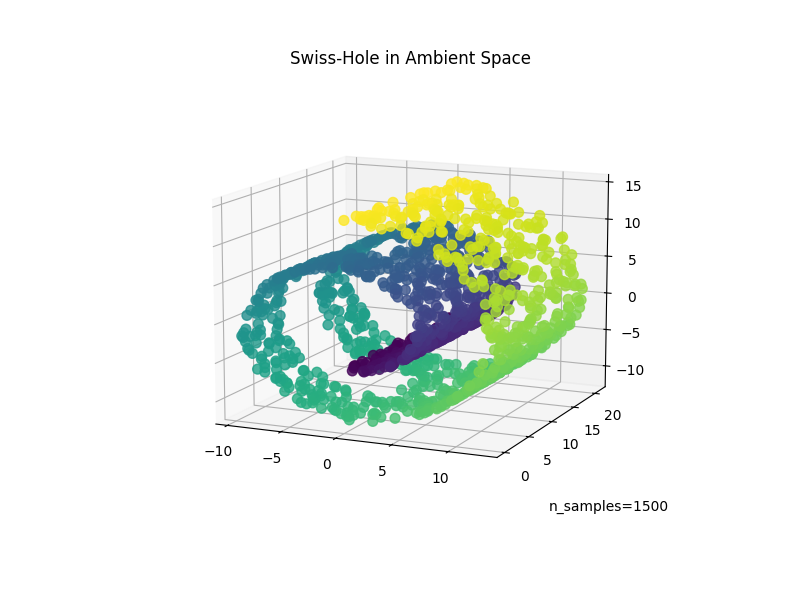
计算LLE和t-SNE嵌入，我们获得了与Swiss Roll类似的结果。LLE非常有能力地展开数据，甚至保留漏洞。t-SNE似乎再次将点的部分聚集在一起，但是，我们注意到，它保留了原始数据的一般布局。

sh_lle, sh_err = manifold.locally_linear_embedding(
    sh_points, n_neighbors=12, n_components=2
)

sh_tsne = manifold.TSNE(
    n_components=2, perplexity=40, init="random", random_state=0
).fit_transform(sh_points)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sh_lle[:, 0], sh_lle[:, 1], c=sh_color)
axs[0].set_title("LLE Embedding of Swiss-Hole")
axs[1].scatter(sh_tsne[:, 0], sh_tsne[:, 1], c=sh_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss-Hole")

LLE Embedding of Swiss-Hole, t-SNE Embedding of Swiss-Hole

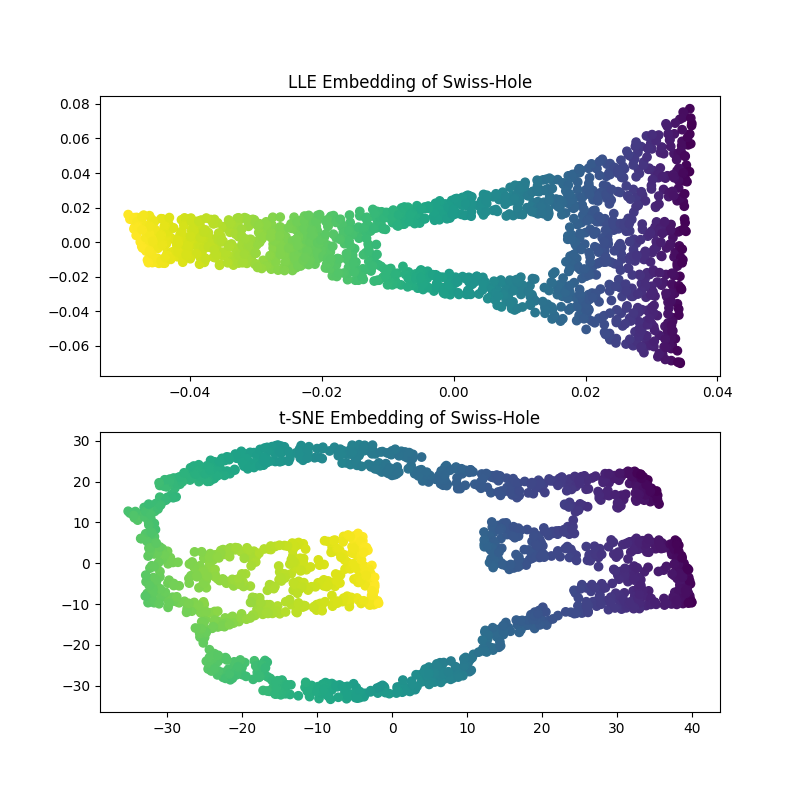
总结发言#

我们注意到，t-SNE受益于测试更多参数组合。通过更好地调整这些参数可能可以获得更好的结果。

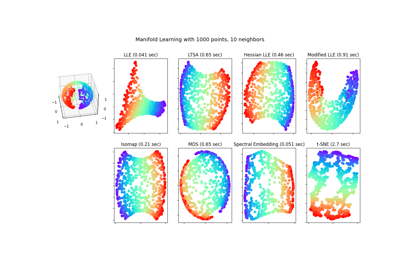
我们观察到，正如“手写数字的Manifold learning”示例中所示，t-SNE在现实世界数据上的表现通常优于LLE。

Total running time of the script: （0分13.378秒）