Lasso、Lasso-LARS和Elastic Net路径#

此示例展示了如何计算沿着Lasso、Lasso-LARS和Elastic Net正规化路径的系数“路径”。换句话说，它显示了正规化参数（Alpha）和系数之间的关系。

Lasso和Lasso-LARS对系数施加了稀疏性约束，鼓励其中一些系数为零。Elastic Net是Lasso的推广，它在L1惩罚项中添加了L2惩罚项。这允许一些系数非零，同时仍然鼓励稀疏性。

Lasso和Elastic Net使用坐标下降法来计算路径，而Lasso-LARS使用LARS算法来计算路径。

路径的计算使用 lasso_path , lars_path ，而且 enet_path .

结果显示了不同的比较图：

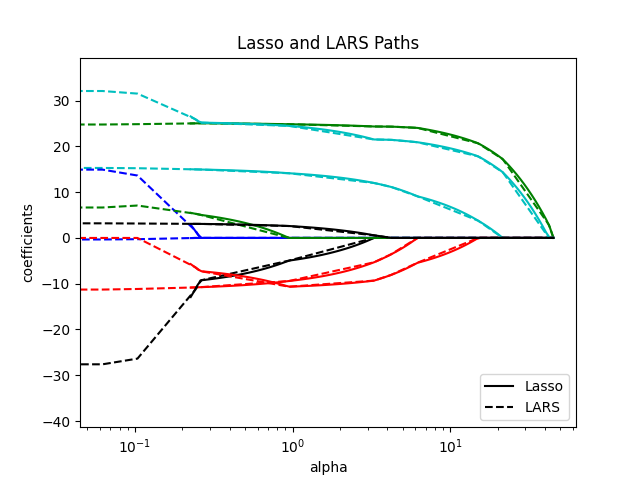
比较Lasso和Lasso-LARS
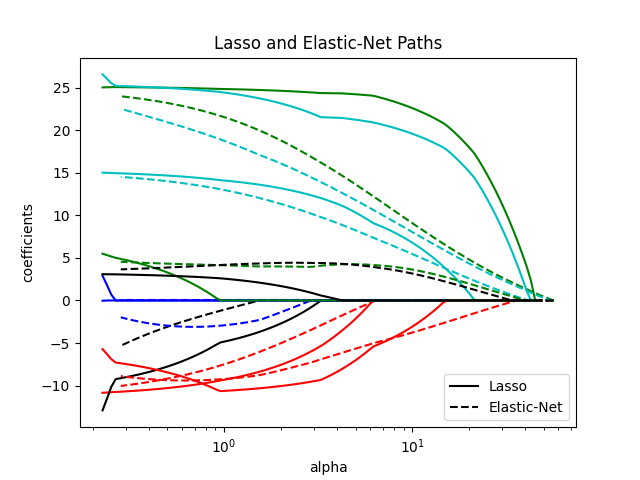
比较Lasso和Elastic Net
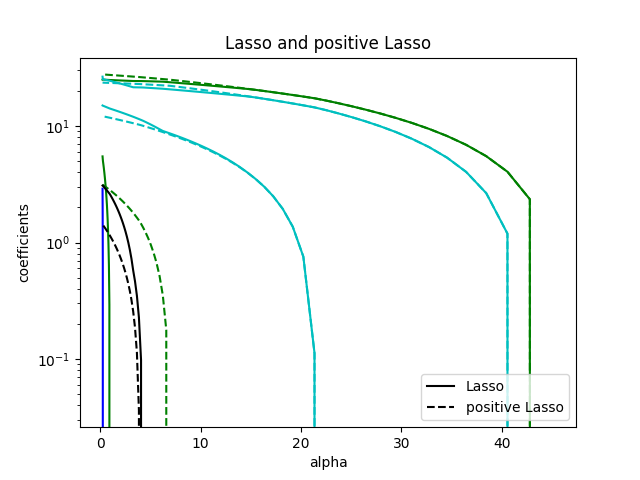
比较Lasso与阳性Lasso
比较LARS和正LARS
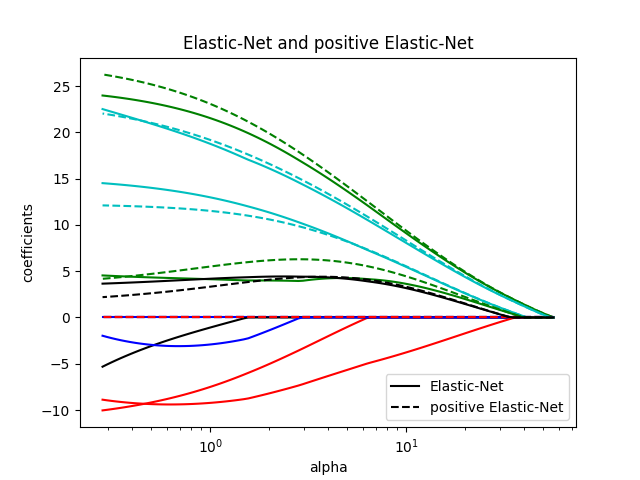
比较弹性网络和正弹性网络

每个图都显示了模型系数如何随着正规化强度的变化而变化，从而深入了解这些模型在不同约束下的行为。

Computing regularization path using the lasso...
Computing regularization path using the positive lasso...
Computing regularization path using the LARS...
Computing regularization path using the positive LARS...
Computing regularization path using the elastic net...
Computing regularization path using the positive elastic net...

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from itertools import cycle

import matplotlib.pyplot as plt

from sklearn.datasets import load_diabetes
from sklearn.linear_model import enet_path, lars_path, lasso_path

X, y = load_diabetes(return_X_y=True)
X /= X.std(axis=0)  # Standardize data (easier to set the l1_ratio parameter)

# Compute paths

eps = 5e-3  # the smaller it is the longer is the path

print("Computing regularization path using the lasso...")
alphas_lasso, coefs_lasso, _ = lasso_path(X, y, eps=eps)

print("Computing regularization path using the positive lasso...")
alphas_positive_lasso, coefs_positive_lasso, _ = lasso_path(
    X, y, eps=eps, positive=True
)

print("Computing regularization path using the LARS...")
alphas_lars, _, coefs_lars = lars_path(X, y, method="lasso")

print("Computing regularization path using the positive LARS...")
alphas_positive_lars, _, coefs_positive_lars = lars_path(
    X, y, method="lasso", positive=True
)

print("Computing regularization path using the elastic net...")
alphas_enet, coefs_enet, _ = enet_path(X, y, eps=eps, l1_ratio=0.8)

print("Computing regularization path using the positive elastic net...")
alphas_positive_enet, coefs_positive_enet, _ = enet_path(
    X, y, eps=eps, l1_ratio=0.8, positive=True
)

# Display results

plt.figure(1)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_lasso, coef_lars, c in zip(coefs_lasso, coefs_lars, colors):
    l1 = plt.semilogx(alphas_lasso, coef_lasso, c=c)
    l2 = plt.semilogx(alphas_lars, coef_lars, linestyle="--", c=c)

plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("Lasso and LARS Paths")
plt.legend((l1[-1], l2[-1]), ("Lasso", "LARS"), loc="lower right")
plt.axis("tight")

plt.figure(2)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_l, coef_e, c in zip(coefs_lasso, coefs_enet, colors):
    l1 = plt.semilogx(alphas_lasso, coef_l, c=c)
    l2 = plt.semilogx(alphas_enet, coef_e, linestyle="--", c=c)

plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("Lasso and Elastic-Net Paths")
plt.legend((l1[-1], l2[-1]), ("Lasso", "Elastic-Net"), loc="lower right")
plt.axis("tight")


plt.figure(3)
for coef_l, coef_pl, c in zip(coefs_lasso, coefs_positive_lasso, colors):
    l1 = plt.semilogy(alphas_lasso, coef_l, c=c)
    l2 = plt.semilogy(alphas_positive_lasso, coef_pl, linestyle="--", c=c)

plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("Lasso and positive Lasso")
plt.legend((l1[-1], l2[-1]), ("Lasso", "positive Lasso"), loc="lower right")
plt.axis("tight")


plt.figure(4)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_lars, coef_positive_lars, c in zip(coefs_lars, coefs_positive_lars, colors):
    l1 = plt.semilogx(alphas_lars, coef_lars, c=c)
    l2 = plt.semilogx(alphas_positive_lars, coef_positive_lars, linestyle="--", c=c)

plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("LARS and Positive LARS")
plt.legend((l1[-1], l2[-1]), ("LARS", "Positive LARS"), loc="lower right")
plt.axis("tight")

plt.figure(5)
for coef_e, coef_pe, c in zip(coefs_enet, coefs_positive_enet, colors):
    l1 = plt.semilogx(alphas_enet, coef_e, c=c)
    l2 = plt.semilogx(alphas_positive_enet, coef_pe, linestyle="--", c=c)

plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("Elastic-Net and positive Elastic-Net")
plt.legend((l1[-1], l2[-1]), ("Elastic-Net", "positive Elastic-Net"), loc="lower right")
plt.axis("tight")
plt.show()

Total running time of the script: （0分0.598秒）