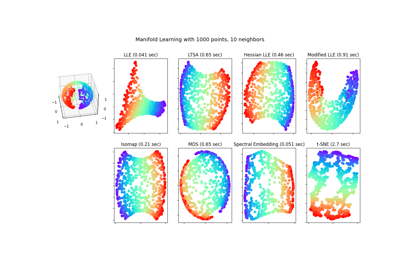
多种学习方法的比较#

使用各种多管学习方法对S曲线数据集进行降维的说明。

有关这些算法的讨论和比较，请参阅 manifold module page

有关方法应用于球体数据集的类似示例，请参阅分割球面上的流形学习方法

请注意，BDS的目的是找到数据的低维表示（这里是2D），其中距离很好地尊重原始多维空间中的距离，与其他Manifold学习算法不同，它不会寻求低维空间中数据的各向同性表示。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

数据集准备#

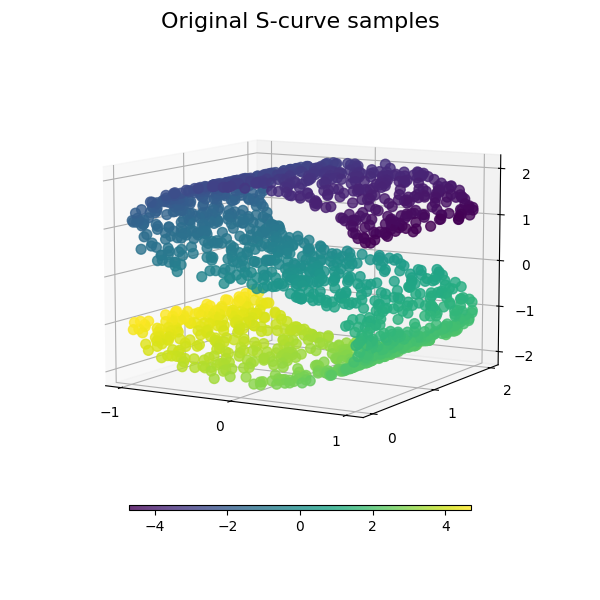
我们首先生成S曲线数据集。

import matplotlib.pyplot as plt

# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d  # noqa: F401
from matplotlib import ticker

from sklearn import datasets, manifold

n_samples = 1500
S_points, S_color = datasets.make_s_curve(n_samples, random_state=0)

我们来看看原始数据。还要定义一些帮助功能，我们将进一步使用这些功能。

def plot_3d(points, points_color, title):
    x, y, z = points.T

    fig, ax = plt.subplots(
        figsize=(6, 6),
        facecolor="white",
        tight_layout=True,
        subplot_kw={"projection": "3d"},
    )
    fig.suptitle(title, size=16)
    col = ax.scatter(x, y, z, c=points_color, s=50, alpha=0.8)
    ax.view_init(azim=-60, elev=9)
    ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
    ax.zaxis.set_major_locator(ticker.MultipleLocator(1))

    fig.colorbar(col, ax=ax, orientation="horizontal", shrink=0.6, aspect=60, pad=0.01)
    plt.show()


def plot_2d(points, points_color, title):
    fig, ax = plt.subplots(figsize=(3, 3), facecolor="white", constrained_layout=True)
    fig.suptitle(title, size=16)
    add_2d_scatter(ax, points, points_color)
    plt.show()


def add_2d_scatter(ax, points, points_color, title=None):
    x, y = points.T
    ax.scatter(x, y, c=points_color, s=50, alpha=0.8)
    ax.set_title(title)
    ax.xaxis.set_major_formatter(ticker.NullFormatter())
    ax.yaxis.set_major_formatter(ticker.NullFormatter())


plot_3d(S_points, S_color, "Original S-curve samples")

定义多管学习的算法#

总管学习是一种非线性降维的方法。这项任务的算法基于这样的想法：许多数据集的维度只是人为的高。

阅读更多的 User Guide .

n_neighbors = 12  # neighborhood which is used to recover the locally linear structure
n_components = 2  # number of coordinates for the manifold

局部线性嵌入#

Locally linear embedding (LLE) can be thought of as a series of local Principal Component Analyses which are globally compared to find the best non-linear embedding. Read more in the User Guide.

params = {
    "n_neighbors": n_neighbors,
    "n_components": n_components,
    "eigen_solver": "auto",
    "random_state": 0,
}

lle_standard = manifold.LocallyLinearEmbedding(method="standard", **params)
S_standard = lle_standard.fit_transform(S_points)

lle_ltsa = manifold.LocallyLinearEmbedding(method="ltsa", **params)
S_ltsa = lle_ltsa.fit_transform(S_points)

lle_hessian = manifold.LocallyLinearEmbedding(method="hessian", **params)
S_hessian = lle_hessian.fit_transform(S_points)

lle_mod = manifold.LocallyLinearEmbedding(method="modified", **params)
S_mod = lle_mod.fit_transform(S_points)

fig, axs = plt.subplots(
    nrows=2, ncols=2, figsize=(7, 7), facecolor="white", constrained_layout=True
)
fig.suptitle("Locally Linear Embeddings", size=16)

lle_methods = [
    ("Standard locally linear embedding", S_standard),
    ("Local tangent space alignment", S_ltsa),
    ("Hessian eigenmap", S_hessian),
    ("Modified locally linear embedding", S_mod),
]
for ax, method in zip(axs.flat, lle_methods):
    name, points = method
    add_2d_scatter(ax, points, S_color, name)

plt.show()

Locally Linear Embeddings, Standard locally linear embedding, Local tangent space alignment, Hessian eigenmap, Modified locally linear embedding

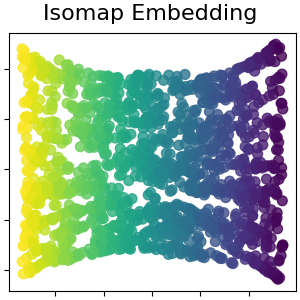
Isomap嵌入#

通过等距映射进行非线性降维。Isomap寻求一种低维嵌入，以保持所有点之间的测地距离。阅读更多的 User Guide .

isomap = manifold.Isomap(n_neighbors=n_neighbors, n_components=n_components, p=1)
S_isomap = isomap.fit_transform(S_points)

plot_2d(S_isomap, S_color, "Isomap Embedding")

多维标度#

多维缩放（SCS）寻求数据的低维表示，其中距离很好地尊重原始多维空间中的距离。阅读更多的 User Guide .

md_scaling = manifold.MDS(
    n_components=n_components,
    max_iter=50,
    n_init=1,
    random_state=0,
    normalized_stress=False,
)
S_scaling = md_scaling.fit_transform(S_points)

plot_2d(S_scaling, S_color, "Multidimensional scaling")

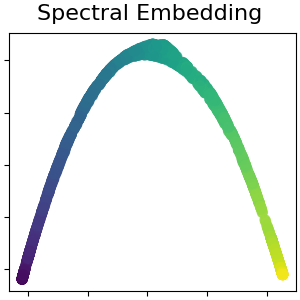
用于非线性降维的谱嵌入#

此实现使用拉普拉斯特征映射，该映射使用拉普拉斯图的谱分解来找到数据的低维表示。阅读更多的 User Guide .

spectral = manifold.SpectralEmbedding(
    n_components=n_components, n_neighbors=n_neighbors, random_state=42
)
S_spectral = spectral.fit_transform(S_points)

plot_2d(S_spectral, S_color, "Spectral Embedding")

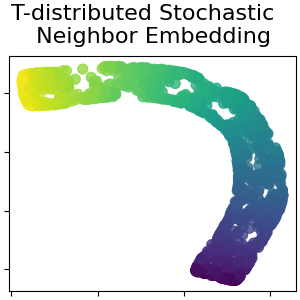
T分布随机邻居嵌入#

它将数据点之间的相似性转换为联合概率，并试图最大限度地减少低维嵌入和高维数据的联合概率之间的Kullback-Leibler偏差。t-SNE的成本函数不是凸的，即通过不同的初始化，我们可以得到不同的结果。阅读更多的 User Guide .

t_sne = manifold.TSNE(
    n_components=n_components,
    perplexity=30,
    init="random",
    max_iter=250,
    random_state=0,
)
S_t_sne = t_sne.fit_transform(S_points)

plot_2d(S_t_sne, S_color, "T-distributed Stochastic  \n Neighbor Embedding")

T-distributed Stochastic Neighbor Embedding

Total running time of the script: （0分9.608秒）