普通最小二乘和岭回归#

普通最小二乘：我们说明了如何使用普通最小二乘（OLS）模型， LinearRegression ，对糖尿病数据集的单个特征。我们对数据的一个子集进行训练，对测试集进行评估，并将预测可视化。
普通最小二乘和岭回归方差：然后，我们通过重复拟合非常小的合成样本，展示了当数据稀疏或有噪声时，OLS如何具有高方差。岭回归， Ridge ，通过惩罚（缩小）系数来减少这种方差，从而产生更稳定的预测。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

数据加载和准备#

加载糖尿病数据集。为了简单起见，我们只在数据中保留一个特征。然后，我们将数据和目标拆分为训练集和测试集。

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split

X, y = load_diabetes(return_X_y=True)
X = X[:, [2]]  # Use only one feature
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, shuffle=False)

线性回归模型#

我们创建一个线性回归模型并将其与训练数据相匹配。请注意，默认情况下，拦截会添加到模型中。我们可以通过设置 fit_intercept 参数.

from sklearn.linear_model import LinearRegression

regressor = LinearRegression().fit(X_train, y_train)

模型评估#

我们使用均方误差和决定系数评估模型在测试集中的性能。

from sklearn.metrics import mean_squared_error, r2_score

y_pred = regressor.predict(X_test)

print(f"Mean squared error: {mean_squared_error(y_test, y_pred):.2f}")
print(f"Coefficient of determination: {r2_score(y_test, y_pred):.2f}")

Mean squared error: 2548.07
Coefficient of determination: 0.47

绘制结果#

最后，我们将火车和测试数据的结果可视化。

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].scatter(X_train, y_train, label="Train data points")
ax[0].plot(
    X_train,
    regressor.predict(X_train),
    linewidth=3,
    color="tab:orange",
    label="Model predictions",
)
ax[0].set(xlabel="Feature", ylabel="Target", title="Train set")
ax[0].legend()

ax[1].scatter(X_test, y_test, label="Test data points")
ax[1].plot(X_test, y_pred, linewidth=3, color="tab:orange", label="Model predictions")
ax[1].set(xlabel="Feature", ylabel="Target", title="Test set")
ax[1].legend()

fig.suptitle("Linear Regression")

plt.show()

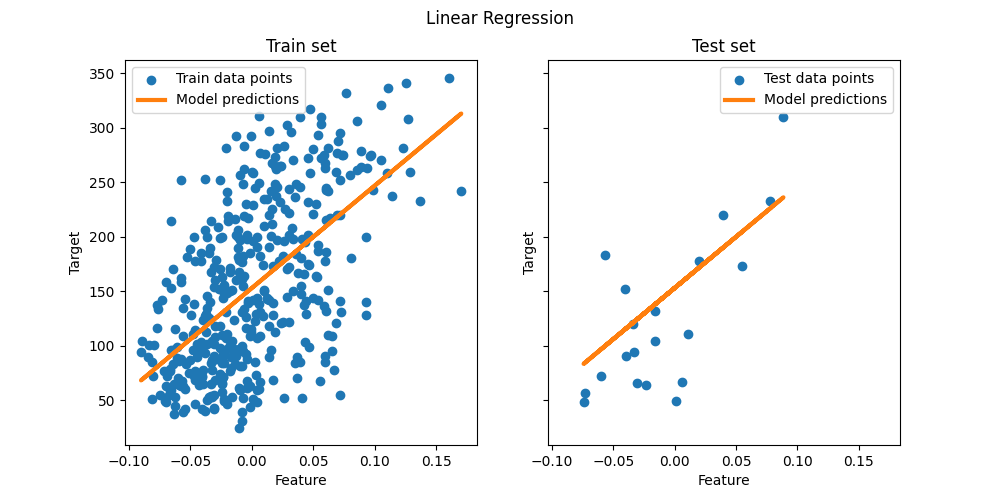
这个单一特征子集上的OLS学习线性函数，该函数可以最大限度地减少训练数据的均方误差。我们可以通过查看测试集的R#2得分和均方误差来了解它的推广效果如何（或较差）。在更高维度中，纯OLS通常过度适合，特别是如果数据有噪音的话。正规化技术（如Ridge或Lasso）可以帮助减少这种情况。

普通最小二乘和岭回归方差#

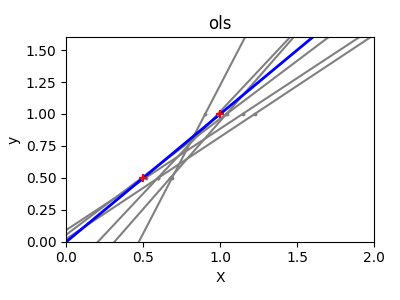
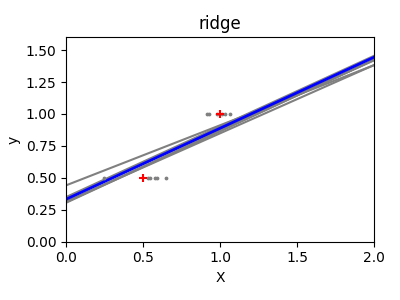
接下来，我们通过使用一个微小的合成数据集更清楚地说明了高方差的问题。我们只对两个数据点进行采样，然后反复向它们添加小的高斯噪声，并重新拟合OLS和Ridge。我们绘制每一条新的线，看看有多少OLS可以跳跃，而岭保持更稳定，由于它的惩罚项。

import matplotlib.pyplot as plt
import numpy as np

from sklearn import linear_model

X_train = np.c_[0.5, 1].T
y_train = [0.5, 1]
X_test = np.c_[0, 2].T

np.random.seed(0)

classifiers = dict(
    ols=linear_model.LinearRegression(), ridge=linear_model.Ridge(alpha=0.1)
)

for name, clf in classifiers.items():
    fig, ax = plt.subplots(figsize=(4, 3))

    for _ in range(6):
        this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
        clf.fit(this_X, y_train)

        ax.plot(X_test, clf.predict(X_test), color="gray")
        ax.scatter(this_X, y_train, s=3, c="gray", marker="o", zorder=10)

    clf.fit(X_train, y_train)
    ax.plot(X_test, clf.predict(X_test), linewidth=2, color="blue")
    ax.scatter(X_train, y_train, s=30, c="red", marker="+", zorder=10)

    ax.set_title(name)
    ax.set_xlim(0, 2)
    ax.set_ylim((0, 1.6))
    ax.set_xlabel("X")
    ax.set_ylabel("y")

    fig.tight_layout()

plt.show()

结论#

在第一个例子中，我们将OLS应用于真实数据集，展示了普通线性模型如何通过最小化训练集的平方误差来适应数据。
在第二个例子中，每次添加噪声时，OLS线都发生剧烈变化，反映了数据稀疏或有噪声时的高方差。相比之下， Ridge 回归引入了一个规则化项，可以缩小系数，稳定预测。

技术如 Ridge 或 Lasso （应用L1罚分）都是提高概括性和减少过度适应的常见方法。当特征相关、数据有噪或样本量小时，调整良好的Ridge或Lasso通常优于纯OLS。

Total running time of the script: （0分0.300秒）