集群绩效评估中的机会调整#

本笔记本探讨了均匀分布的随机标签对一些集群评估指标行为的影响。为此，使用固定数量的样本并作为估计器分配的集群数量的函数来计算指标。该示例分为两个实验：

第一个实验，使用固定的“地面真值标签”（以及因此固定数量的类）和随机的“预测标签”;
第二个实验，使用不同的“基本真相标签”、随机的“预测标签”。“预测标签”具有与“地面真相标签”相同数量的类和集群。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

定义要评估的指标列表#

聚类算法基本上是无监督的学习方法。然而，由于我们在这个例子中为合成聚类分配了类标签，因此可以使用评估指标来利用这个“监督”的地面实况信息来量化结果聚类的质量。这些指标的例子如下：

V-度量，完整性和齐性的调和平均值;
兰德指数，衡量数据点对根据集群算法和地面真值类别分配的结果一致分组的频率;
调整后的兰德指数（ARI），机会调整后的兰德指数，使得随机集群分配的ARI预期为0.0;
互信息（MI）是一种信息论指标，可以量化两个标签的依赖程度。请注意，完美标记的MI最大值取决于集群和样本的数量;
规范化互信息（NMI），定义在大量数据点限制下的0（无互信息）和1（完美匹配标签分配，直到标签的排列）之间的互信息。它没有根据偶然性进行调整：那么聚集数据点的数量不够大，随机标记的MI或NMI的预期值可能显着非零;
调整后的相互信息（AMI），一种机会调整后的相互信息。与ARI类似，随机集群分配的AMI预期为0.0。

更多详见集群绩效评估 module.

from sklearn import metrics

score_funcs = [
    ("V-measure", metrics.v_measure_score),
    ("Rand index", metrics.rand_score),
    ("ARI", metrics.adjusted_rand_score),
    ("MI", metrics.mutual_info_score),
    ("NMI", metrics.normalized_mutual_info_score),
    ("AMI", metrics.adjusted_mutual_info_score),
]

第一个实验：固定地面真实标签和增加集群数量#

我们首先定义一个创建均匀分布随机标签的函数。

import numpy as np

rng = np.random.RandomState(0)

def random_labels(n_samples, n_classes):
    return rng.randint(low=0, high=n_classes, size=n_samples)

另一个函数将使用 random_labels 创建固定的基本真相标签集的函数 (labels_a ）分布在 n_classes 然后对几组随机“预测”的标签进行评分 (labels_b ）评估给定指标在给定条件下的变异性 n_clusters .

def fixed_classes_uniform_labelings_scores(
    score_func, n_samples, n_clusters_range, n_classes, n_runs=5
):
    scores = np.zeros((len(n_clusters_range), n_runs))
    labels_a = random_labels(n_samples=n_samples, n_classes=n_classes)

    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

在第一个示例中，我们将类的数量（集群的真实数量）设置为 n_classes=10 .集群的数量因提供的值而异 n_clusters_range .

import matplotlib.pyplot as plt
import seaborn as sns

n_samples = 1000
n_classes = 10
n_clusters_range = np.linspace(2, 100, 10).astype(int)
plots = []
names = []

sns.color_palette("colorblind")
plt.figure(1)

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = fixed_classes_uniform_labelings_scores(
        score_func, n_samples, n_clusters_range, n_classes=n_classes
    )
    plots.append(
        plt.errorbar(
            n_clusters_range,
            scores.mean(axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=1,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "Clustering measures for random uniform labeling\n"
    f"against reference assignment with {n_classes} classes"
)
plt.xlabel(f"Number of clusters (Number of samples is fixed to {n_samples})")
plt.ylabel("Score value")
plt.ylim(bottom=-0.05, top=1.05)
plt.legend(plots, names, bbox_to_anchor=(0.5, 0.5))
plt.show()

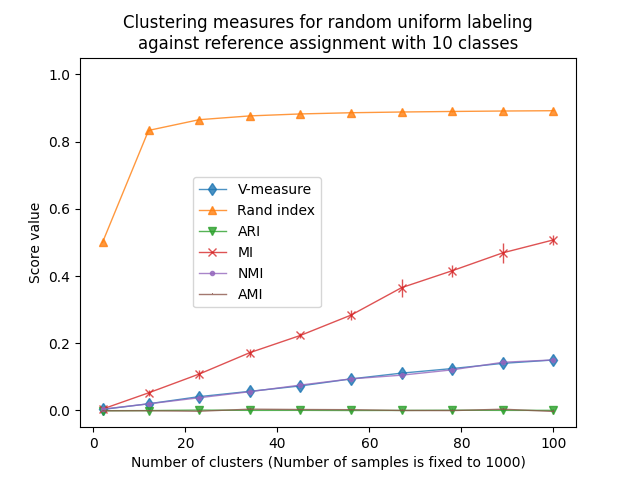
Clustering measures for random uniform labeling against reference assignment with 10 classes

兰德指数饱和 n_clusters > n_classes .其他未经调整的测量，例如V-测量，显示集群数量和样本数量之间的线性依赖性。

根据机会测量（例如ARI和AMI）进行调整后，显示出一些以平均分0.0为中心的随机变化，与样本和集群的数量无关。

第二个实验：不同数量的类和集群#

在本节中，我们定义了一个类似的函数，该函数使用多个指标来对2个均匀分布的随机标签进行评分。在这种情况下，将为中的每个可能值匹配类数量和分配的集群数量 n_clusters_range .

def uniform_labelings_scores(score_func, n_samples, n_clusters_range, n_runs=5):
    scores = np.zeros((len(n_clusters_range), n_runs))

    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_a = random_labels(n_samples=n_samples, n_classes=n_clusters)
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

在这种情况下，我们使用 n_samples=100 以显示具有与样本数量相似或等于的集群数量的影响。

n_samples = 100
n_clusters_range = np.linspace(2, n_samples, 10).astype(int)

plt.figure(2)

plots = []
names = []

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = uniform_labelings_scores(score_func, n_samples, n_clusters_range)
    plots.append(
        plt.errorbar(
            n_clusters_range,
            np.median(scores, axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=2,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "Clustering measures for 2 random uniform labelings\nwith equal number of clusters"
)
plt.xlabel(f"Number of clusters (Number of samples is fixed to {n_samples})")
plt.ylabel("Score value")
plt.legend(plots, names)
plt.ylim(bottom=-0.05, top=1.05)
plt.show()

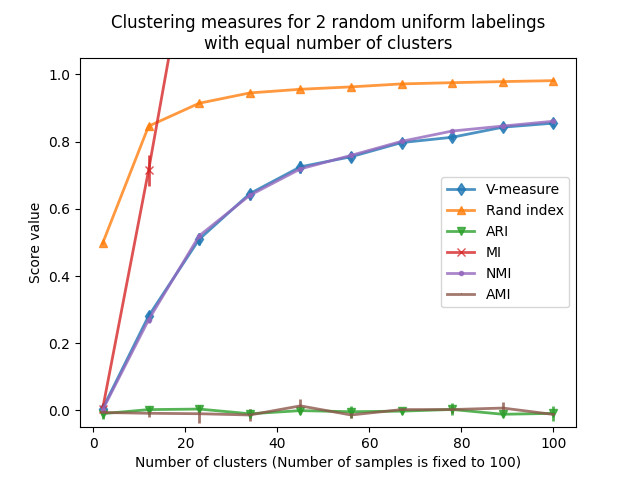
Clustering measures for 2 random uniform labelings with equal number of clusters

我们观察到与第一个实验类似的结果：调整后的机会指标始终保持在零附近，而其他指标往往会随着更细粒度的标签而变得更大。随机标记的平均V度量随着聚类的数量接近用于计算度量的样本总数而显著增加。此外，原始互信息从上到下是无界的，其规模取决于聚类问题的维度和地面真值类的基数。这就是为什么曲线会偏离图表。

因此，只有调整后的测量才能安全地用作共识指数，以评估数据集的各个重叠子样本上给定k值的集群算法的平均稳定性。

因此，未经调整的集群评估指标可能会具有误导性，因为它们为细粒度标签输出了很大的值，人们可能会认为标签已经捕获了有意义的群体，而它们可能是完全随机的。特别是，此类未经调整的指标不应用于比较输出不同数量集群的不同集群算法的结果。

Total running time of the script: （0分0.816秒）