k均值假设的证明

这个例子旨在说明k均值产生不直观且可能不理想的集群的情况。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

数据生成

功能 make_blobs 生成各向同性（球形）高斯斑点。为了获得各向异性（椭圆）高斯斑点，必须定义线性 transformation .

import numpy as np

from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # Anisotropic blobs
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # Unequal variance
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

我们可以将结果数据可视化：

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("Mixture of Gaussian Blobs")

axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("Unequal Variance")

axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Ground truth clusters").set_y(0.95)
plt.show()

匹配模型和绘图结果

之前生成的数据现在用于显示如何 KMeans 在以下情况下表现：

• 非最佳集群数量：在真实环境中，没有唯一定义的 true 集群的数量。必须根据基于数据的标准和对预期目标的了解来决定适当数量的集群。

• 各向异性分布斑点：k均值包括最小化样本到分配给它们的集群重心的欧几里得距离。因此，k均值更适合于各向同性且正态分布的集群（即球形高斯）。

• 不等方差：k均值相当于对方差相同但均值可能不同的k个高斯分布的“混合”取最大似然估计量。

• 大小不均匀的斑点：没有关于k-均值的理论结果表明它需要相似的集群大小才能表现良好，但最小化欧几里得距离确实意味着问题越稀疏和多维，运行具有不同重心种子的算法的需要就越高，以确保全球最小惯性。

from sklearn.cluster import KMeans

common_params = {
    "n_init": "auto",
    "random_state": random_state,
}

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

y_pred = KMeans(n_clusters=2, **common_params).fit_predict(X)
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y_pred)
axs[0, 0].set_title("Non-optimal Number of Clusters")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_aniso)
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_varied)
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
axs[1, 0].set_title("Unequal Variance")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_filtered)
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Unexpected KMeans clusters").set_y(0.95)
plt.show()

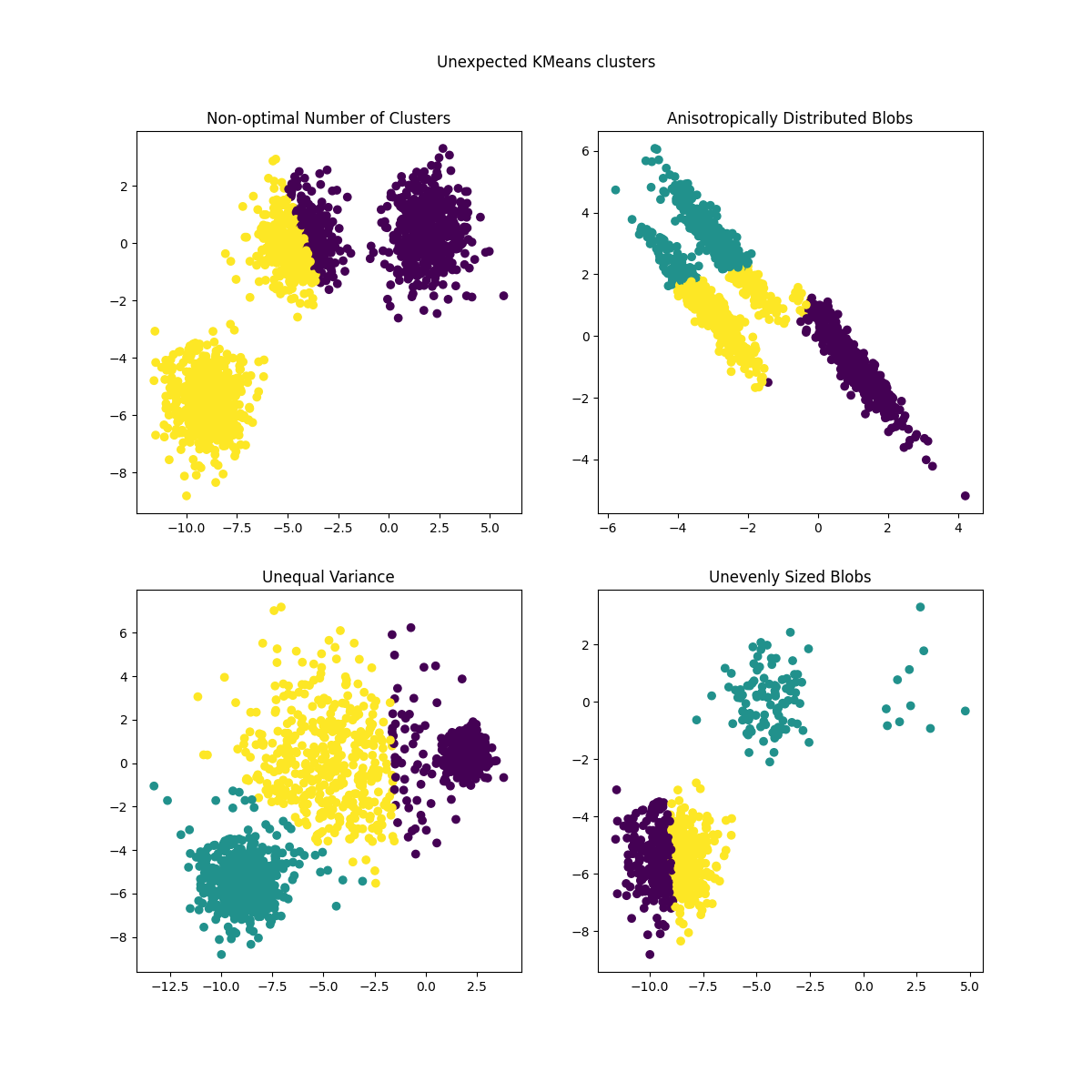
可能的解决方案

有关如何找到正确数量的斑点的示例，请参阅 在KMeans聚类中使用轮廓分析选择聚类数 .在这种情况下，只需设置 n_clusters=3 .

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Optimal Number of Clusters")
plt.show()

为了处理大小不均匀的斑点，可以增加随机初始化的数量。在这种情况下，我们设置 n_init=10 以避免找到次优的局部最小值。For more details see 使用k均值对稀疏数据进行聚集 .

y_pred = KMeans(n_clusters=3, n_init=10, random_state=random_state).fit_predict(
    X_filtered
)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs \nwith several initializations")
plt.show()

由于各向异性和不等方差是k均值算法的真正局限性，因此在这里我们建议使用 GaussianMixture ，它还假设高斯集群，但不对其方差施加任何限制。请注意，仍然必须找到正确的斑点数量（请参阅 高斯混合模型选择 ).

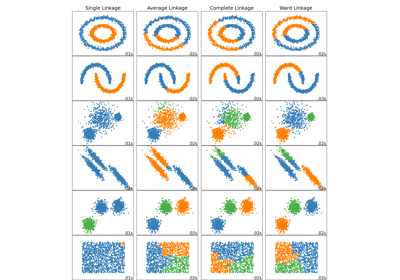
有关其他集群方法如何处理各向异性或不等方差斑点的示例，请参阅示例 在玩具数据集上比较不同的聚类算法 .

from sklearn.mixture import GaussianMixture

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))

y_pred = GaussianMixture(n_components=3).fit_predict(X_aniso)
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
ax1.set_title("Anisotropically Distributed Blobs")

y_pred = GaussianMixture(n_components=3).fit_predict(X_varied)
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
ax2.set_title("Unequal Variance")

plt.suptitle("Gaussian mixture clusters").set_y(0.95)
plt.show()

最后发言

在多维空间中，欧几里得距离往往会变得膨胀（本例中未显示）。在k均值集群之前运行降维算法可以缓解这个问题并加速计算（请参阅示例 基于k-means的文本聚类 ).

在已知集群是各向同性的、具有相似的方差并且不是太稀疏的情况下，k均值算法非常有效，并且是可用的最快的集群算法之一。如果必须重新启动多次以避免收敛到局部最小值，那么这个优势就会消失。

相关实例

二分K均值和常规K均值性能比较

Bisecting K-Means and Regular K-Means Performance Comparison

在玩具数据集上比较不同的分层链接方法

Comparing different hierarchical linkage methods on toy datasets

绘制交叉验证预测

Plotting Cross-Validated Predictions

不同核的先验和后验高斯过程的说明

Illustration of prior and posterior Gaussian process for different kernels