稳健协方差估计和Mahalanobis距离相关性#

此示例显示了高斯分布数据上使用Mahalanobis距离的协方差估计。

对于高斯分布数据，观察的距离 \(x_i\) 分布模式可以使用其Mahalanobis距离计算：

\[d_{(\mu,\Sigma)}(x_i)^2 = (x_i - \mu)^T\Sigma^{-1}(x_i - \mu)\]

哪里 \(\mu\) 和 \(\Sigma\) 是基础高斯分布的位置和协方差。

在实践中， \(\mu\) 和 \(\Sigma\) 被一些估计所取代。标准协方差最大似然估计（MLE）对数据集中是否存在异常值非常敏感，因此下游马哈拉诺比斯距离也非常敏感。最好使用稳健的协方差估计器，以确保估计能够抵抗数据集中的“错误”观察，并且计算出的马哈拉诺比斯距离准确反映观察的真实组织。

The Minimum Covariance Determinant estimator (MCD) is a robust, high-breakdown point (i.e. it can be used to estimate the covariance matrix of highly contaminated datasets, up to \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) outliers) estimator of covariance. The idea behind the MCD is to find \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) observations whose empirical covariance has the smallest determinant, yielding a "pure" subset of observations from which to compute standards estimates of location and covariance. The MCD was introduced by P.J.Rousseuw in [1].

此示例说明了Mahalanobis距离如何受到外围数据的影响。当使用基于Mahalanobis距离的标准协方差MLE时，从污染分布中得出的观测结果与从真实高斯分布中得出的观测结果无法区分。使用基于CCD的Mahalanobis距离，这两个群体变得可区分。相关应用包括异常值检测、观察排名和集群。

备注

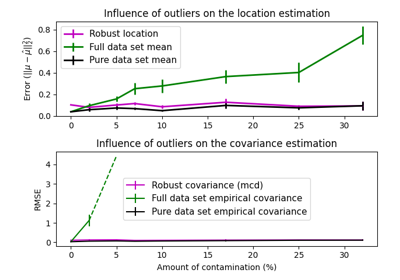
另见稳健与经验协方差估计

引用

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

生成数据#

首先，我们生成一个包含125个样本和2个特征的数据集。两个特征都是高斯分布，平均值为0，但特征1的标准差等于2，特征2的标准差等于1。接下来，用高斯离群值样本替换25个样本，其中特征1的标准差等于1，特征2的标准差等于7。

import numpy as np

# for consistent results
np.random.seed(7)

n_samples = 125
n_outliers = 25
n_features = 2

# generate Gaussian data of shape (125, 2)
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.0
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.0
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)

结果比较#

下面，我们将基于BCD和MLE的协方差估计量与我们的数据进行匹配，并打印估计的协方差矩阵。请注意，基于MLE的估计器（7.5）的特征2的估计方差远高于MCB稳健估计器（1.2）的估计方差。这表明基于MCB的鲁棒估计器对异常值样本的抵抗力更强，这些样本旨在在特征2中具有更大的方差。

import matplotlib.pyplot as plt

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# fit a MCD robust estimator to data
robust_cov = MinCovDet().fit(X)
# fit a MLE estimator to data
emp_cov = EmpiricalCovariance().fit(X)
print(
    "Estimated covariance matrix:\nMCD (Robust):\n{}\nMLE:\n{}".format(
        robust_cov.covariance_, emp_cov.covariance_
    )
)

Estimated covariance matrix:
MCD (Robust):
[[ 3.26253567e+00 -3.06695631e-03]
 [-3.06695631e-03  1.22747343e+00]]
MLE:
[[ 3.23773583 -0.24640578]
 [-0.24640578  7.51963999]]

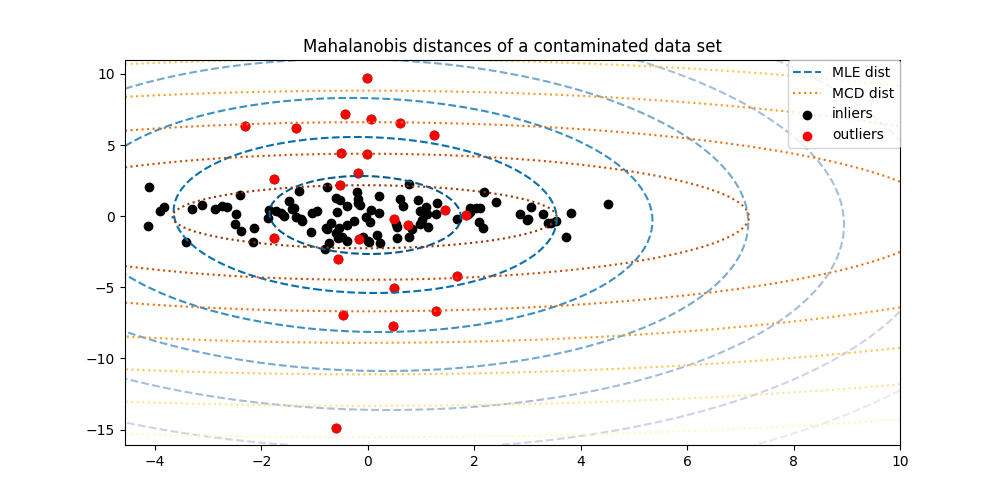
为了更好地可视化差异，我们绘制了通过两种方法计算的Mahalanobis距离的轮廓。请注意，基于稳健的MCB的Mahalanobis距离更好地适合内点黑点，而基于MLE的距离更受异常点的影响。

import matplotlib.lines as mlines

fig, ax = plt.subplots(figsize=(10, 5))
# Plot data set
inlier_plot = ax.scatter(X[:, 0], X[:, 1], color="black", label="inliers")
outlier_plot = ax.scatter(
    X[:, 0][-n_outliers:], X[:, 1][-n_outliers:], color="red", label="outliers"
)
ax.set_xlim(ax.get_xlim()[0], 10.0)
ax.set_title("Mahalanobis distances of a contaminated data set")

# Create meshgrid of feature 1 and feature 2 values
xx, yy = np.meshgrid(
    np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
    np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
# Calculate the MLE based Mahalanobis distances of the meshgrid
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
    xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles="dashed"
)
# Calculate the MCD based Mahalanobis distances
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(
    xx, yy, np.sqrt(mahal_robust_cov), cmap=plt.cm.YlOrBr_r, linestyles="dotted"
)

# Add legend
ax.legend(
    [
        mlines.Line2D([], [], color="tab:blue", linestyle="dashed"),
        mlines.Line2D([], [], color="tab:orange", linestyle="dotted"),
        inlier_plot,
        outlier_plot,
    ],
    ["MLE dist", "MCD dist", "inliers", "outliers"],
    loc="upper right",
    borderaxespad=0,
)

plt.show()

Mahalanobis distances of a contaminated data set

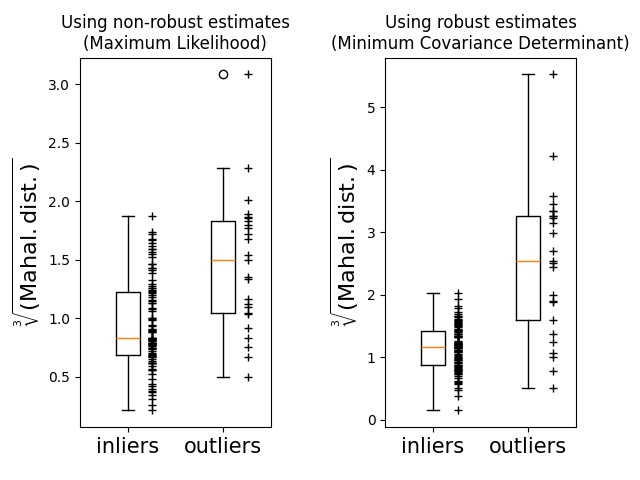
最后，我们强调了基于MCB的Mahalanobis距离区分离群值的能力。我们取Mahalanobis距离的三次根，产生大约正态分布（正如Wilson和Hilferty所建议的那样 [2]) ，然后用箱形图绘制内点和离群点样本的值。对于稳健的基于MCB的Mahalanobis距离，离群点样本的分布与内点样本的分布更加分离。

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=0.6)

# Calculate cubic root of MLE Mahalanobis distances for samples
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# Plot boxplots
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax1.plot(
    np.full(n_samples - n_outliers, 1.26),
    emp_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax1.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("Using non-robust estimates\n(Maximum Likelihood)")

# Calculate cubic root of MCD Mahalanobis distances for samples
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# Plot boxplots
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax2.plot(
    np.full(n_samples - n_outliers, 1.26),
    robust_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax2.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("Using robust estimates\n(Minimum Covariance Determinant)")

plt.show()

Using non-robust estimates (Maximum Likelihood), Using robust estimates (Minimum Covariance Determinant)

Total running time of the script: （0分0.202秒）