RBF SVM参数#

此示例说明了参数的影响 gamma 和 C 径向基函数（RBF）核SVM。

直觉上， gamma 参数定义了单个训练示例的影响力达到的程度，低值意味着“远”，高值意味着“近”。的 gamma 参数可以被看作是由模型选择作为支持向量的样本的影响半径的倒数。

的 C 参数权衡训练示例的正确分类与决策函数裕度的最大化。对于更大的价值 C 如果决策函数在正确分类所有训练点方面更好，则将接受更小的裕度。较低 C 将鼓励更大的裕度，因此更简单的决策功能，但以牺牲训练准确性为代价。换句话说 C 充当支持机器人支持器中的规则化参数。

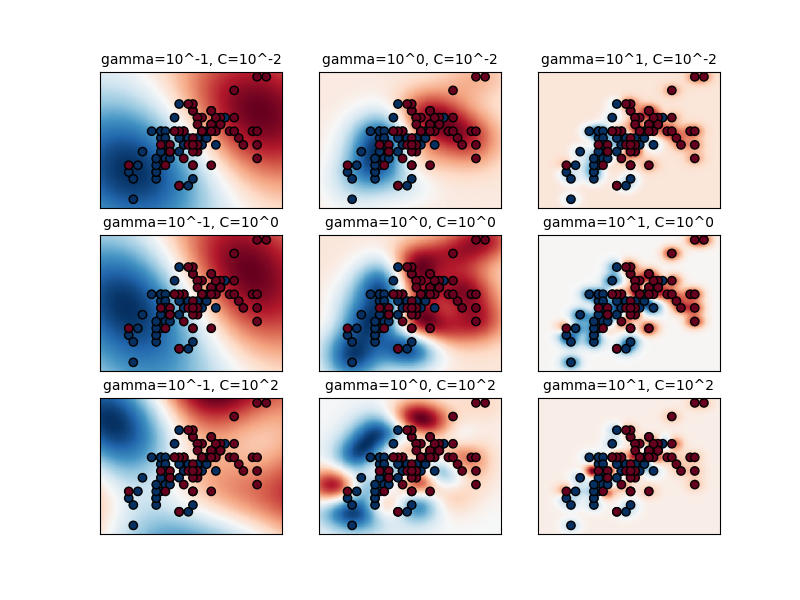
第一个图是简化分类问题上各种参数值的决策函数的可视化，该问题仅涉及2个输入特征和2个可能的目标类别（二元分类）。请注意，对于具有更多要素或目标类的问题，这种绘图不可能执行。

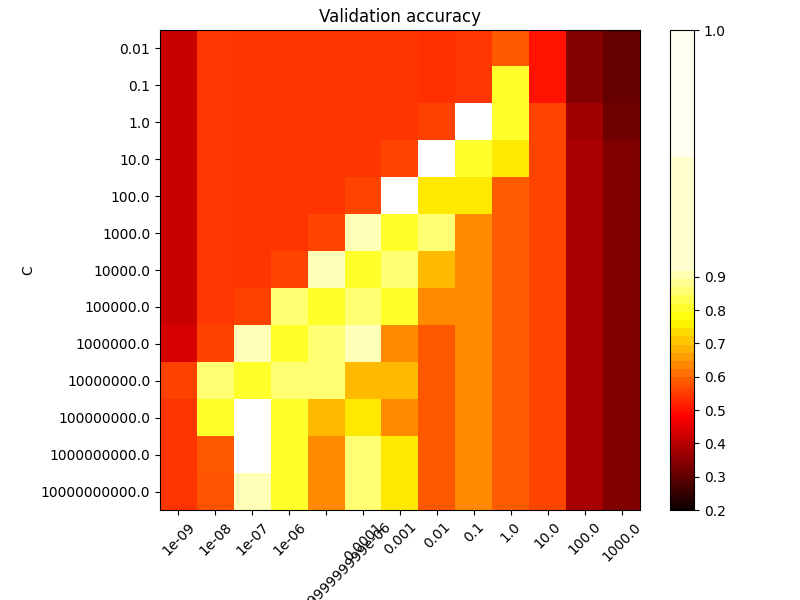
第二个图是分类器的交叉验证准确度的热图，其为 C 和 gamma .对于这个例子，我们探索了一个相对较大的网格以供说明。在实践中，来自 \(10^{-3}\) 到 \(10^3\) 通常就足够了。如果最佳参数位于网格边界，则可以在后续搜索中向该方向扩展。

请注意，热图图有一个特殊的彩色条，其中点值接近表现最佳模型的得分值，以便在眨眼之间轻松区分它们。

模型的行为对 gamma 参数.如果 gamma 太大时，支持量的影响区域半径仅包括支持量本身，而没有进行任何正规化 C 将能够防止过度贴合。

当 gamma 非常小，模型受到太多限制，无法捕捉数据的复杂性或“形状”。任何选择的支持载体的影响区域都将包括整个训练集。产生的模型将与线性模型类似，线性模型具有一组超平面，这些超平面将任何两个类别对的高密度中心分开。

对于中间值，我们可以在第二个图中看到，好的模型可以在 C 和 gamma .光滑型号（较低 gamma 值）可以通过增加正确分类每个点的重要性（更大 C 值）因此是表现良好的模型的对角线。

最后，人们还可以观察到，对于的一些中间值 gamma 当我们获得性能相同的模型时， C 变得非常大。这表明支持载体集不再改变。单独的RBS核半径可以充当良好的结构调节器。增加 C 进一步没有帮助，可能是因为不再有违反训练点（在余量内或错误分类），或者至少找不到更好的解决方案。在分数相等的情况下，使用较小的可能是有意义的 C 价值观，因为非常高 C 值通常会增加试穿时间。

另一方面，更低 C 值通常会导致更多的支持载体，这可能会增加预测时间。因此，降低 C 涉及适应时间和预测时间之间的权衡。

我们还应该注意到，分数的微小差异是由交叉验证过程的随机分割引起的。可以通过增加CV迭代次数来消除这些虚假变化 n_splits 以计算时间为代价。增加的值数量 C_range 和 gamma_range 步骤将提高超参数热图的分辨率。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

实用程序类将色彩图的中点移动到感兴趣的值周围。

import numpy as np
from matplotlib.colors import Normalize


class MidpointNormalize(Normalize):
    def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
        self.midpoint = midpoint
        Normalize.__init__(self, vmin, vmax, clip)

    def __call__(self, value, clip=None):
        x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
        return np.ma.masked_array(np.interp(value, x, y))

加载和准备数据集#

网格搜索数据集

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

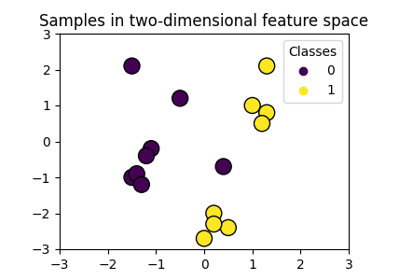
决策函数可视化的数据集：我们仅保留X中的前两个特征，并对数据集进行子采样，以仅保留2个类，使其成为二进制分类问题。

X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1

扩展数据以进行支持机训练通常是一个好主意。在这个例子中，我们在扩展所有数据时有点作弊，而不是在训练集上适应转换并只是将其应用于测试集。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)

训练分类器#

对于初始搜索，以10为底的对数网格通常很有帮助。使用以2为基，可以实现更细的调整，但成本要高得多。

from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
from sklearn.svm import SVC

C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

print(
    "The best parameters are %s with a score of %0.2f"
    % (grid.best_params_, grid.best_score_)
)

The best parameters are {'C': np.float64(1.0), 'gamma': np.float64(0.1)} with a score of 0.97

现在我们需要为2D版本中的所有参数适应分类器（我们在这里使用了一组较小的参数，因为训练需要一段时间）

C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
    for gamma in gamma_2d_range:
        clf = SVC(C=C, gamma=gamma)
        clf.fit(X_2d, y_2d)
        classifiers.append((C, gamma, clf))

可视化#

绘制参数效果的可视化

import matplotlib.pyplot as plt

plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for k, (C, gamma, clf) in enumerate(classifiers):
    # evaluate decision function in a grid
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # visualize decision function for these parameters
    plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
    plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)), size="medium")

    # visualize parameter's effect on decision function
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
    plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r, edgecolors="k")
    plt.xticks(())
    plt.yticks(())
    plt.axis("tight")

scores = grid.cv_results_["mean_test_score"].reshape(len(C_range), len(gamma_range))

gamma=10^-1, C=10^-2, gamma=10^0, C=10^-2, gamma=10^1, C=10^-2, gamma=10^-1, C=10^0, gamma=10^0, C=10^0, gamma=10^1, C=10^0, gamma=10^-1, C=10^2, gamma=10^0, C=10^2, gamma=10^1, C=10^2

绘制验证准确度随伽玛和C的函数的热图

分数被编码为具有从暗红色到亮黄色变化的热色图的颜色。由于最有趣的分数都位于0.92到0.97的范围内，我们使用自定义归一化器将中点设置为0.92，以便更容易可视化有趣范围内分数值的微小变化，同时不会将所有低分数值粗暴地折叠为相同的颜色。

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=0.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(
    scores,
    interpolation="nearest",
    cmap=plt.cm.hot,
    norm=MidpointNormalize(vmin=0.2, midpoint=0.92),
)
plt.xlabel("gamma")
plt.ylabel("C")
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title("Validation accuracy")
plt.show()

Total running time of the script: （0分3.742秒）