基于L1的稀疏信号模型#

本示例比较了三个基于l1的回归模型，该模型针对从稀疏和相关特征获得的合成信号，这些特征进一步被添加性高斯噪音破坏：

众所周知，由于不相关变量与相关变量不太相关，当数据维度增加时，Lasso估计会变得接近模型选择估计。在存在相关特征的情况下，Lasso本身无法选择正确的稀疏模式 [1].

在这里，我们比较了三种型号的性能 $R^2$ 与实际情况相比，评分、匹配时间和估计系数的稀疏性。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

生成合成数据集#

我们生成一个样本数量低于特征总数的数据集。这导致欠定系统，即解不是唯一的，因此我们不能应用普通最小二乘本身。正规化为目标函数引入了惩罚项，这修改了优化问题，并有助于减轻系统的欠定性质。

目标 y 是具有交替符号的线性组合。只有100个频率中最低的10个 X 用于生成 y ，而其余功能则不提供信息。这会产生一个多维稀疏特征空间，其中需要一定程度的l1惩罚。

import numpy as np

rng = np.random.RandomState(0)
n_samples, n_features, n_informative = 50, 100, 10
time_step = np.linspace(-2, 2, n_samples)
freqs = 2 * np.pi * np.sort(rng.rand(n_features)) / 0.01
X = np.zeros((n_samples, n_features))

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step)

idx = np.arange(n_features)
true_coef = (-1) ** idx * np.exp(-idx / 10)
true_coef[n_informative:] = 0  # sparsify coef
y = np.dot(X, true_coef)

一些信息特征具有接近的频率来引发（反）相关性。

freqs[:n_informative]

array([ 2.9502547 , 11.8059798 , 12.63394388, 12.70359377, 24.62241605,
       37.84077985, 40.30506066, 44.63327171, 54.74495357, 59.02456369])

使用引入随机阶段 numpy.random.random_sample 和一些高斯噪音（由 numpy.random.normal ）添加到功能和目标中。

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step + 2 * (rng.random_sample() - 0.5))
    X[:, i] += 0.2 * rng.normal(0, 1, n_samples)

y += 0.2 * rng.normal(0, 1, n_samples)

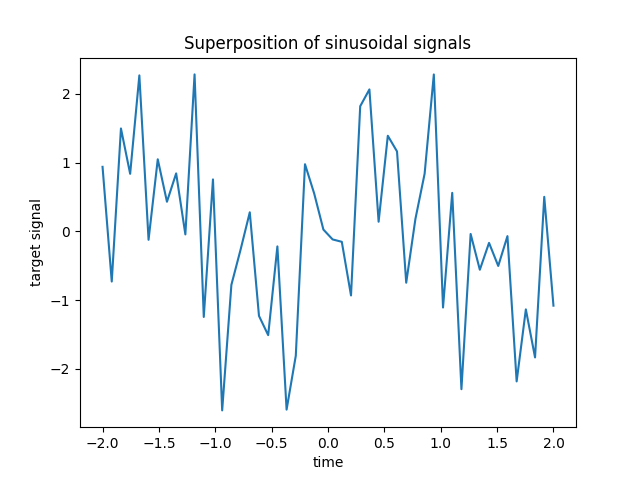
例如，可以从监测一些环境变量的传感器节点中获得这种稀疏、有噪和相关的特征，因为它们通常根据其位置（空间相关性）记录类似的值。我们可以想象目标。

import matplotlib.pyplot as plt

plt.plot(time_step, y)
plt.ylabel("target signal")
plt.xlabel("time")
_ = plt.title("Superposition of sinusoidal signals")

为了简单起见，我们将数据分为训练集和测试集。实际上应该使用 TimeSeriesSplit 交叉验证以估计测试分数的方差。我们在这里设置 shuffle="False" 因为在处理具有时间关系的数据时，我们决不能使用接替测试数据的训练数据。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=False)

在下文中，我们根据适合度计算三个基于l1的模型的性能 $R^2$ 分数和合适的时间。然后我们制作一个图来比较估计系数与地面真值系数的稀疏性，最后我们分析之前的结果。

Lasso#

在这个例子中，我们演示了一个 Lasso 具有固定值的正规化参数 alpha .在实践中，最佳参数 alpha 应通过a选择 TimeSeriesSplit 交叉验证策略 LassoCV .为了使示例执行起来简单快捷，我们在这里直接设置了Alpha的最佳值。

from time import time

from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score

t0 = time()
lasso = Lasso(alpha=0.14).fit(X_train, y_train)
print(f"Lasso fit done in {(time() - t0):.3f}s")

y_pred_lasso = lasso.predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(f"Lasso r^2 on test data : {r2_score_lasso:.3f}")

Lasso fit done in 0.001s
Lasso r^2 on test data : 0.480

自动相关性确定（ARD）#

ARD回归是Lasso的混蛋版本。如果需要，它可以为所有参数（包括误差方差）生成区间估计。当信号具有高斯噪音时，这是一个合适的选择。查看示例比较线性Bayesian回归量用于比较 ARDRegression 和 BayesianRidge 回归者。

from sklearn.linear_model import ARDRegression

t0 = time()
ard = ARDRegression().fit(X_train, y_train)
print(f"ARD fit done in {(time() - t0):.3f}s")

y_pred_ard = ard.predict(X_test)
r2_score_ard = r2_score(y_test, y_pred_ard)
print(f"ARD r^2 on test data : {r2_score_ard:.3f}")

ARD fit done in 0.008s
ARD r^2 on test data : 0.543

ElasticNet#

ElasticNet 是之间的中间立场 Lasso 和 Ridge ，因为它结合了L1和L2惩罚。正则化的量由两个超参数控制 l1_ratio 和 alpha .为 l1_ratio = 0 惩罚是纯L2，模型相当于a Ridge .同样， l1_ratio = 1 是一个纯L1惩罚，该模型相当于一个 Lasso .为 0 < l1_ratio < 1 ，点球是L1和L2的组合。

与之前所做的一样，我们用固定值训练模型 alpha 和 l1_ratio .为了选择它们的最佳值，我们使用了 ElasticNetCV ，为了保持示例简单，此处未显示。

from sklearn.linear_model import ElasticNet

t0 = time()
enet = ElasticNet(alpha=0.08, l1_ratio=0.5).fit(X_train, y_train)
print(f"ElasticNet fit done in {(time() - t0):.3f}s")

y_pred_enet = enet.predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(f"ElasticNet r^2 on test data : {r2_score_enet:.3f}")

ElasticNet fit done in 0.001s
ElasticNet r^2 on test data : 0.636

结果的绘图和分析#

在本节中，我们使用热图来可视化各个线性模型的真实系数和估计系数的稀疏性。

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.colors import SymLogNorm

df = pd.DataFrame(
    {
        "True coefficients": true_coef,
        "Lasso": lasso.coef_,
        "ARDRegression": ard.coef_,
        "ElasticNet": enet.coef_,
    }
)

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-1, vmax=1),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.title(
    f"Models' coefficients\nLasso $R^2$: {r2_score_lasso:.3f}, "
    f"ARD $R^2$: {r2_score_ard:.3f}, "
    f"ElasticNet $R^2$: {r2_score_enet:.3f}"
)
plt.tight_layout()

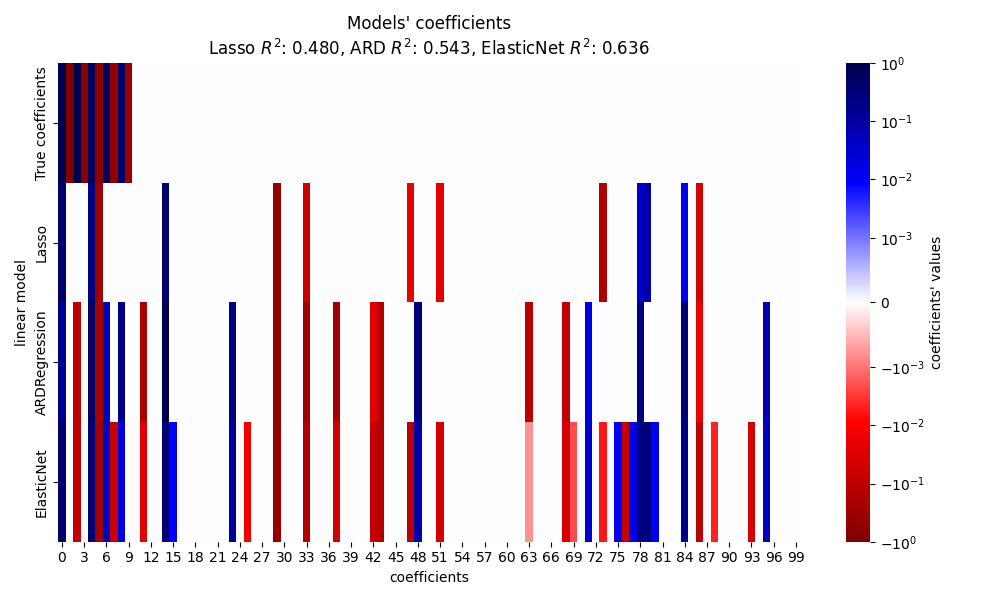
Models' coefficients Lasso $R^2$: 0.480, ARD $R^2$: 0.543, ElasticNet $R^2$: 0.636

在本示例中 ElasticNet 产生最好的分数并捕捉到大部分预测特征，但仍然无法找到所有真实的成分。请注意，两者 ElasticNet 和 ARDRegression 导致模型稀疏度低于 Lasso .

结论#

Lasso 众所周知，它可以有效恢复稀疏数据，但在高度相关的特征下表现不佳。事实上，如果几个相关的特征对目标有贡献， Lasso 最终会选择其中的一个。在稀疏但不相关的特征的情况下， Lasso 模型会更合适。

ElasticNet 在系数上引入了一些稀疏性，并将其值缩小为零。因此，在存在对目标有贡献的相关特征的情况下，模型仍然能够减少它们的权重，而无需将它们完全设置为零。这导致模型比纯模型更稀疏 Lasso 并且也可以捕获非预测性特征。

ARDRegression 在处理高斯噪音时效果更好，但仍然无法处理相关特征，并且由于匹配先验而需要更大量的时间。

引用#

Total running time of the script: （0分0.302秒）