手写数字的流形学习：局部线性嵌入，Isomap...#

我们在数字数据集上展示了各种嵌入技术。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

加载数字数据集#

我们将加载数字数据集，并且仅使用十个可用类中的前六个。

from sklearn.datasets import load_digits

digits = load_digits(n_class=6)
X, y = digits.data, digits.target
n_samples, n_features = X.shape
n_neighbors = 30

我们可以绘制该数据集中的前一百位数字。

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
    ax.imshow(X[idx].reshape((8, 8)), cmap=plt.cm.binary)
    ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)

A selection from the 64-dimensional digits dataset

绘图嵌入的助手功能#

下面，我们将使用不同的技术来嵌入数字数据集。我们将绘制原始数据在每个嵌入上的投影。它将允许我们检查或数字是否在嵌入空间中分组在一起，或者分散在其中。

import numpy as np
from matplotlib import offsetbox

from sklearn.preprocessing import MinMaxScaler


def plot_embedding(X, title):
    _, ax = plt.subplots()
    X = MinMaxScaler().fit_transform(X)

    for digit in digits.target_names:
        ax.scatter(
            *X[y == digit].T,
            marker=f"${digit}$",
            s=60,
            color=plt.cm.Dark2(digit),
            alpha=0.425,
            zorder=2,
        )
    shown_images = np.array([[1.0, 1.0]])  # just something big
    for i in range(X.shape[0]):
        # plot every digit on the embedding
        # show an annotation box for a group of digits
        dist = np.sum((X[i] - shown_images) ** 2, 1)
        if np.min(dist) < 4e-3:
            # don't show points that are too close
            continue
        shown_images = np.concatenate([shown_images, [X[i]]], axis=0)
        imagebox = offsetbox.AnnotationBbox(
            offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r), X[i]
        )
        imagebox.set(zorder=1)
        ax.add_artist(imagebox)

    ax.set_title(title)
    ax.axis("off")

嵌入技术比较#

下面，我们比较了不同的技术。然而，有几件事需要注意：

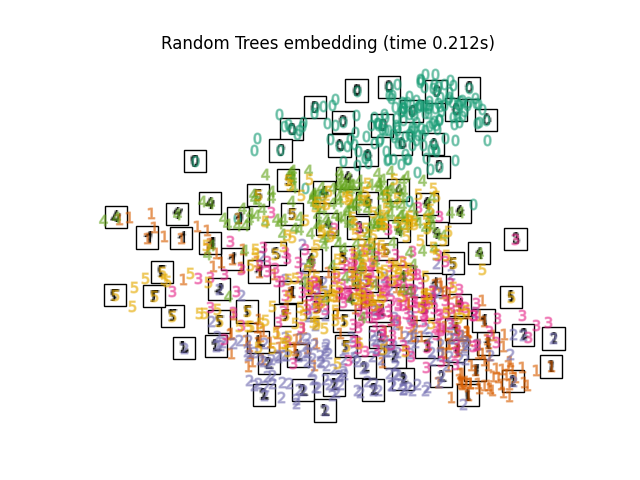
的 RandomTreesEmbedding 从技术上讲，它并不是一种多维嵌入方法，因为它学习我们在其上应用了降维方法的多维表示。然而，将数据集转换为类线性可分离的表示通常很有用。
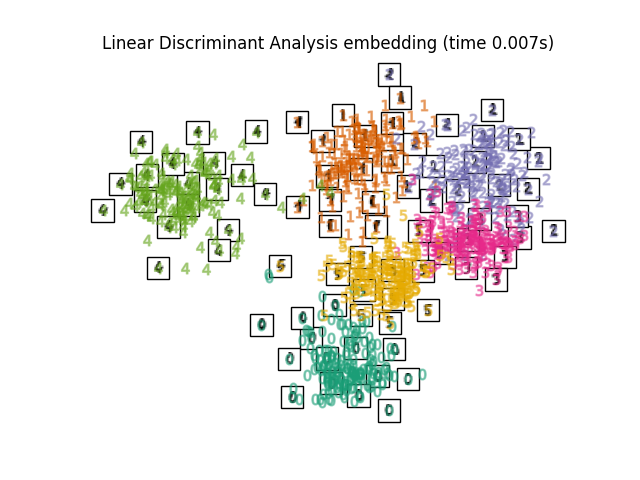
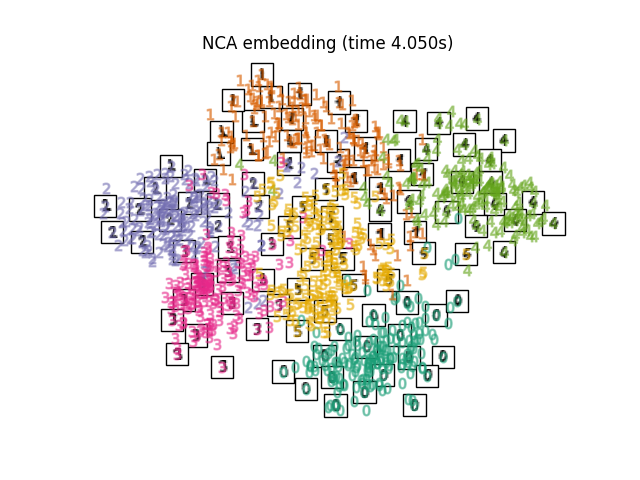
的 LinearDiscriminantAnalysis 和 NeighborhoodComponentsAnalysis ，是有监督的维度约简方法，即它们利用提供的标签，与其他方法相反。
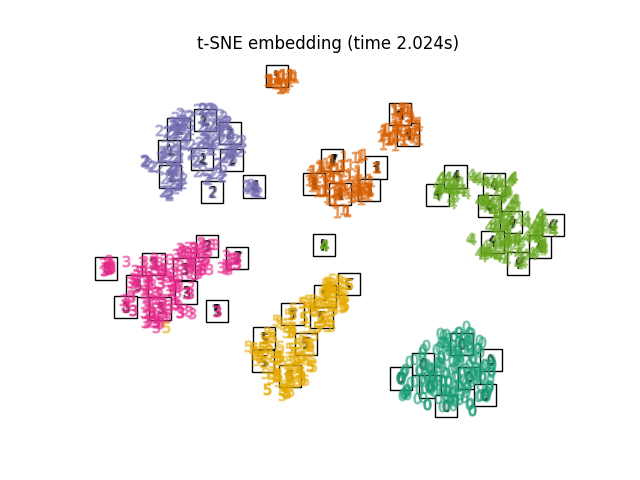
的 TSNE 在本示例中使用PCA生成的嵌入来初始化。它确保嵌入的全局稳定性，即嵌入不依赖于随机初始化。

from sklearn.decomposition import TruncatedSVD
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.ensemble import RandomTreesEmbedding
from sklearn.manifold import (
    MDS,
    TSNE,
    Isomap,
    LocallyLinearEmbedding,
    SpectralEmbedding,
)
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.random_projection import SparseRandomProjection

embeddings = {
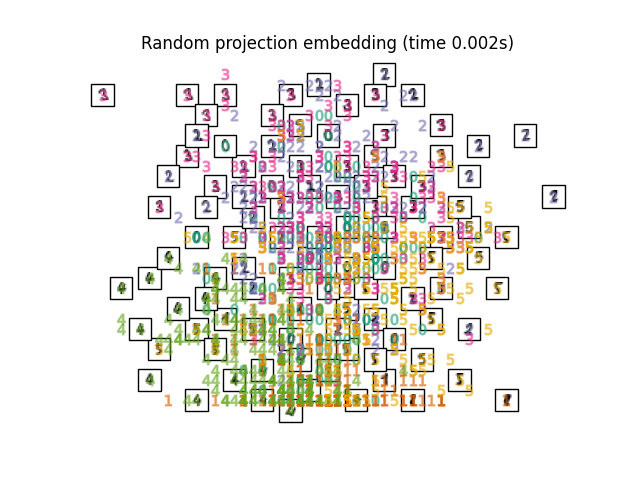
    "Random projection embedding": SparseRandomProjection(
        n_components=2, random_state=42
    ),
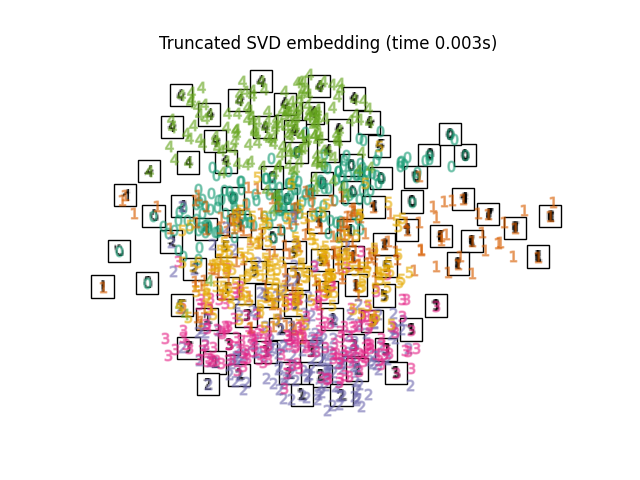
    "Truncated SVD embedding": TruncatedSVD(n_components=2),
    "Linear Discriminant Analysis embedding": LinearDiscriminantAnalysis(
        n_components=2
    ),
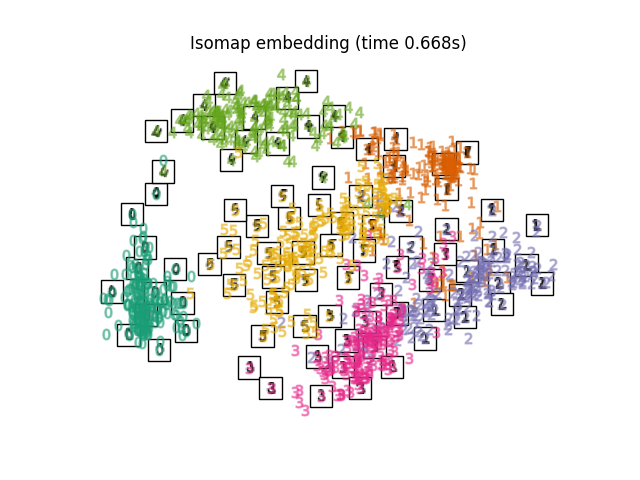
    "Isomap embedding": Isomap(n_neighbors=n_neighbors, n_components=2),
    "Standard LLE embedding": LocallyLinearEmbedding(
        n_neighbors=n_neighbors, n_components=2, method="standard"
    ),
    "Modified LLE embedding": LocallyLinearEmbedding(
        n_neighbors=n_neighbors, n_components=2, method="modified"
    ),
    "Hessian LLE embedding": LocallyLinearEmbedding(
        n_neighbors=n_neighbors, n_components=2, method="hessian"
    ),
    "LTSA LLE embedding": LocallyLinearEmbedding(
        n_neighbors=n_neighbors, n_components=2, method="ltsa"
    ),
    "MDS embedding": MDS(n_components=2, n_init=1, max_iter=120, eps=1e-6),
    "Random Trees embedding": make_pipeline(
        RandomTreesEmbedding(n_estimators=200, max_depth=5, random_state=0),
        TruncatedSVD(n_components=2),
    ),
    "Spectral embedding": SpectralEmbedding(
        n_components=2, random_state=0, eigen_solver="arpack"
    ),
    "t-SNE embedding": TSNE(
        n_components=2,
        max_iter=500,
        n_iter_without_progress=150,
        n_jobs=2,
        random_state=0,
    ),
    "NCA embedding": NeighborhoodComponentsAnalysis(
        n_components=2, init="pca", random_state=0
    ),
}

一旦我们声明了所有感兴趣的方法，我们就可以运行并执行原始数据的投影。我们将存储投影数据以及执行每次投影所需的计算时间。

from time import time

projections, timing = {}, {}
for name, transformer in embeddings.items():
    if name.startswith("Linear Discriminant Analysis"):
        data = X.copy()
        data.flat[:: X.shape[1] + 1] += 0.01  # Make X invertible
    else:
        data = X

    print(f"Computing {name}...")
    start_time = time()
    projections[name] = transformer.fit_transform(data, y)
    timing[name] = time() - start_time

Computing Random projection embedding...
Computing Truncated SVD embedding...
Computing Linear Discriminant Analysis embedding...
Computing Isomap embedding...
Computing Standard LLE embedding...
Computing Modified LLE embedding...
Computing Hessian LLE embedding...
Computing LTSA LLE embedding...
Computing MDS embedding...
Computing Random Trees embedding...
Computing Spectral embedding...
Computing t-SNE embedding...
Computing NCA embedding...

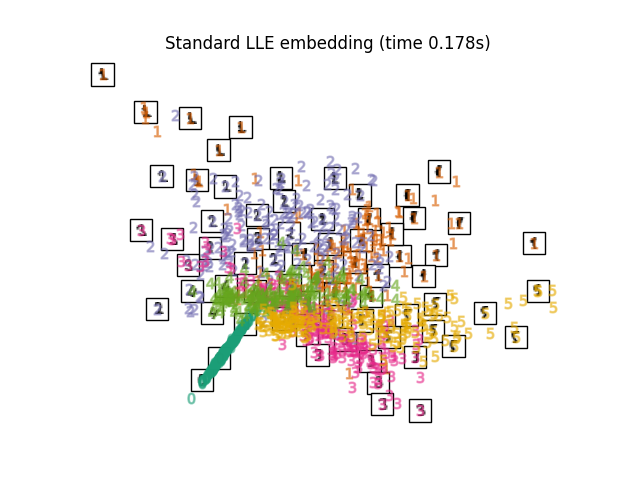
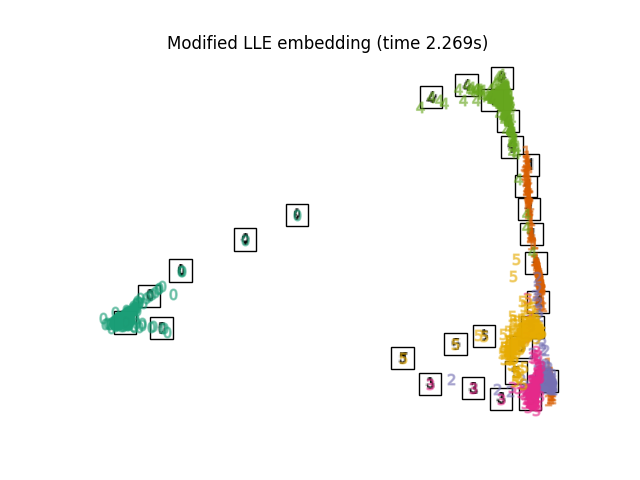
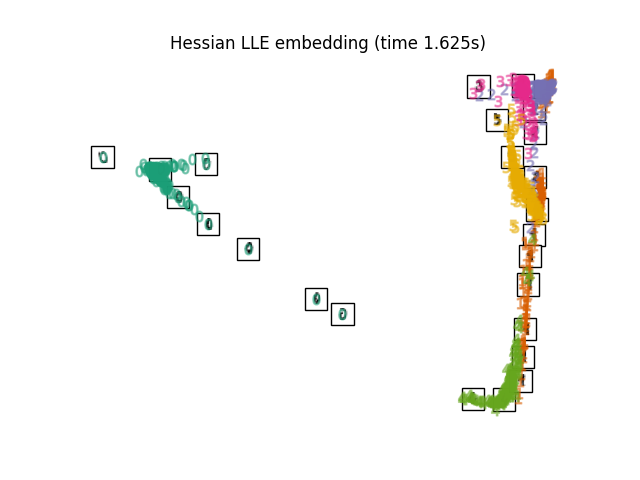
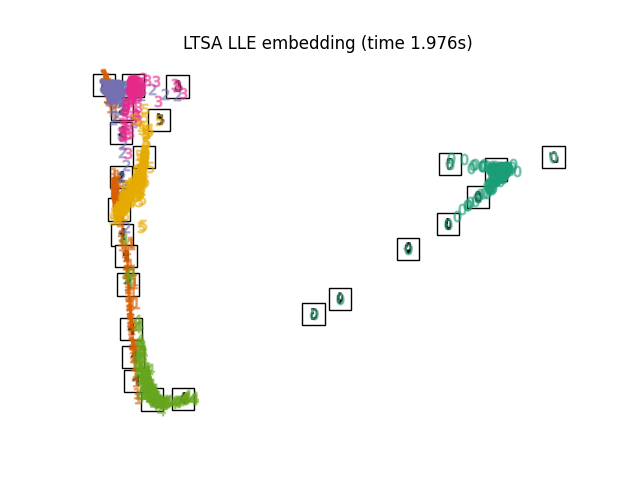
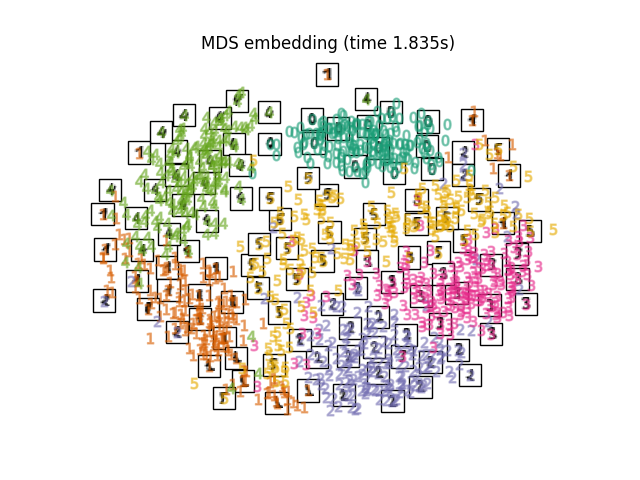
最后，我们可以绘制出每种方法给出的投影。

for name in timing:
    title = f"{name} (time {timing[name]:.3f}s)"
    plot_embedding(projections[name], title)

plt.show()

Total running time of the script: (0 minutes 18.451 seconds)