备注

Go to the end 下载完整的示例代码。或者通过浏览器中的MysterLite或Binder运行此示例

梯度Boosting回归的预测区间#

此示例展示了如何使用分位数回归来创建预测区间。看到梯度增强树的梯度中的功能例如，展示的一些其他功能 HistGradientBoostingRegressor .

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

通过将函数f应用于均匀采样的随机输入来生成合成回归问题的一些数据。

import numpy as np

from sklearn.model_selection import train_test_split


def f(x):
    """The function to predict."""
    return x * np.sin(x)


rng = np.random.RandomState(42)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()

为了让问题变得有趣，我们生成目标y的观测值，作为由函数f计算的确定性项和跟随中心的随机噪音项的和 log-normal .为了使其变得更加有趣，我们考虑噪音幅度取决于输入变量x（异方差噪音）的情况。

log正态分布是非对称且长尾的：观察到大的异常值是可能的，但不可能观察到小的异常值。

sigma = 0.5 + X.ravel() / 10
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2 / 2)
y = expected_y + noise

拆分为训练、测试数据集：

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

匹配非线性分位数和最小平方回归量#

用分位数损失和阿尔法=0.05、0.5、0.95训练的梯度增强模型。

对于Alpha=0.05和Alpha=0.95获得的模型产生90%的置信区间（95% - 5% = 90%）。

用Alpha=0.5训练的模型会产生中位数的回归：平均而言，高于和低于预测值的目标观察值应该相同数量。

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_pinball_loss, mean_squared_error

all_models = {}
common_params = dict(
    learning_rate=0.05,
    n_estimators=200,
    max_depth=2,
    min_samples_leaf=9,
    min_samples_split=9,
)
for alpha in [0.05, 0.5, 0.95]:
    gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, **common_params)
    all_models["q %1.2f" % alpha] = gbr.fit(X_train, y_train)

注意到 HistGradientBoostingRegressor 远快于 GradientBoostingRegressor 从中间数据集开始 (n_samples >= 10_000 ），而本示例的情况并非如此。

为了比较起见，我们还对用通常的（均值）平方误差（SSE）训练的基线模型进行了匹配。

gbr_ls = GradientBoostingRegressor(loss="squared_error", **common_params)
all_models["mse"] = gbr_ls.fit(X_train, y_train)

创建跨越 [0, 10] 范围

xx = np.atleast_2d(np.linspace(0, 10, 1000)).T

绘制真实的条件均值函数f、条件均值的预测值（损失等于平方误差）、条件中位数和条件90%区间（从第5个条件均值到第95个条件均值）。

import matplotlib.pyplot as plt

y_pred = all_models["mse"].predict(xx)
y_lower = all_models["q 0.05"].predict(xx)
y_upper = all_models["q 0.95"].predict(xx)
y_med = all_models["q 0.50"].predict(xx)

fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.plot(xx, y_med, "tab:orange", linewidth=3, label="Predicted median")
plt.plot(xx, y_pred, "tab:green", linewidth=3, label="Predicted mean")
plt.fill_between(
    xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.show()

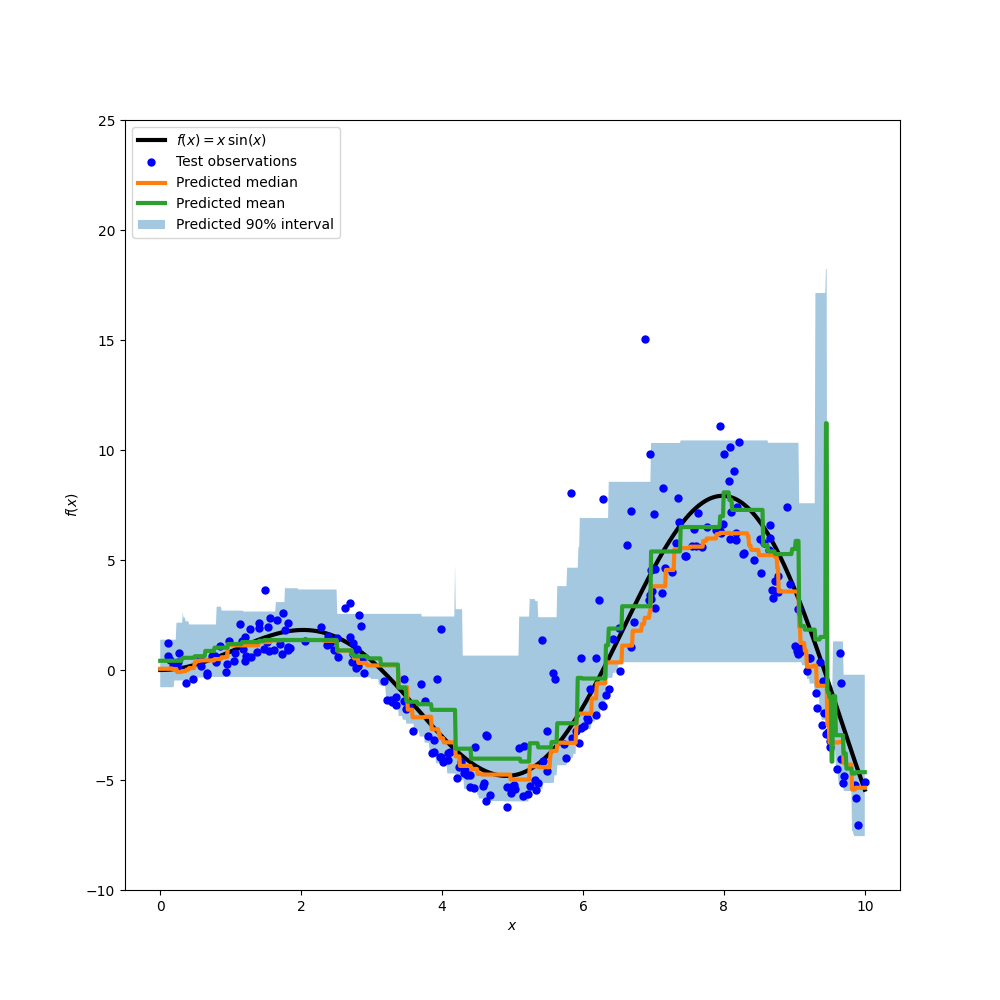
将预测中位数与预测平均值进行比较，我们注意到中位数平均低于平均值，因为噪音偏向高值（大异常值）。中位数估计似乎也更平稳，因为它对异常值具有天然的鲁棒性。

另请注意，不幸的是，梯度增强树的感性偏差阻止了我们的0.05分位数完全捕获信号的sinoisoal形状，特别是在x=8附近。调整超参数可以减少这种影响，如本笔记本的最后一部分所示。

错误指标分析#

用以下方法测量模型 mean_squared_error 和 mean_pinball_loss 训练数据集上的指标。

import pandas as pd


def highlight_min(x):
    x_min = x.min()
    return ["font-weight: bold" if v == x_min else "" for v in x]


results = []
for name, gbr in sorted(all_models.items()):
    metrics = {"model": name}
    y_pred = gbr.predict(X_train)
    for alpha in [0.05, 0.5, 0.95]:
        metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_train, y_pred, alpha=alpha)
    metrics["MSE"] = mean_squared_error(y_train, y_pred)
    results.append(metrics)

pd.DataFrame(results).set_index("model").style.apply(highlight_min)

	pbl=0.05	pbl=0.50	pbl=0.95	MSE
model
mse	0.715413	0.715413	0.715413	7.750348
q 0.05	0.127128	1.253445	2.379763	18.933253
q 0.50	0.305438	0.622811	0.940184	9.827917
q 0.95	3.909909	2.145957	0.382005	28.667219

一列显示了使用相同指标评估的所有模型。当使用相同的指标训练和测量模型时，应获得列上的最小数字。如果训练收敛，那么训练集中的情况应该始终如此。

请注意，由于目标分布是不对称的，预期的条件均值和条件中位数显著不同，因此无法使用平方误差模型获得条件中位数的良好估计，反之亦然。

如果目标分布是对称的并且没有异常值（例如具有高斯噪音），那么中位数估计器和最小平方估计器将产生类似的预测。

然后我们在测试集上做同样的事情。

results = []
for name, gbr in sorted(all_models.items()):
    metrics = {"model": name}
    y_pred = gbr.predict(X_test)
    for alpha in [0.05, 0.5, 0.95]:
        metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_test, y_pred, alpha=alpha)
    metrics["MSE"] = mean_squared_error(y_test, y_pred)
    results.append(metrics)

pd.DataFrame(results).set_index("model").style.apply(highlight_min)

	pbl=0.05	pbl=0.50	pbl=0.95	MSE
model
mse	0.917281	0.767498	0.617715	6.692901
q 0.05	0.144204	1.245961	2.347717	15.648026
q 0.50	0.412021	0.607752	0.803483	5.874771
q 0.95	4.354394	2.355445	0.356497	34.852774

误差更高，这意味着模型稍微过度适合数据。它仍然表明，当通过最小化同一度量来训练模型时，可以获得最佳测试度量。

请注意，条件中位数估计量在测试集上的MSE方面与平方误差估计量具有竞争力：这可以通过平方误差估计量对可能导致显著过拟合的大离群值非常敏感的事实来解释。这可以在前一个图的右侧看到。条件中值估计是有偏的（对这种不对称噪声的低估），但对离群值和过拟合也很稳健。

置信区间的校准#

我们还可以评估两个极端分位数估计器产生经过良好校准的条件90%置信区间的能力。

为此，我们可以计算落在预测之间的观测值的比例：

def coverage_fraction(y, y_low, y_high):
    return np.mean(np.logical_and(y >= y_low, y <= y_high))


coverage_fraction(
    y_train,
    all_models["q 0.05"].predict(X_train),
    all_models["q 0.95"].predict(X_train),
)

np.float64(0.9)

在训练集中，校准非常接近90%置信区间的预期覆盖值。

coverage_fraction(
    y_test, all_models["q 0.05"].predict(X_test), all_models["q 0.95"].predict(X_test)
)

np.float64(0.868)

在测试集中，估计的置信区间稍微太窄。然而，请注意，我们需要将这些指标包裹在交叉验证循环中，以评估它们在数据重新分配下的变异性。

调整分位数回归量的超参数#

在上面的图中，我们观察到第5百分位回归量似乎不适合并且无法适应信号的曲线形状。

该模型的超参数是针对中位数回归量近似手动调整的，并且没有理由相同的超参数适用于第5百分位回归量。

为了证实这一假设，我们通过对Alpha=0.05的弹球损失进行交叉验证来选择最佳模型参数来调整第5百分位数的新回归量的超参数：

from pprint import pprint

from sklearn.experimental import enable_halving_search_cv  # noqa: F401
from sklearn.metrics import make_scorer
from sklearn.model_selection import HalvingRandomSearchCV

param_grid = dict(
    learning_rate=[0.05, 0.1, 0.2],
    max_depth=[2, 5, 10],
    min_samples_leaf=[1, 5, 10, 20],
    min_samples_split=[5, 10, 20, 30, 50],
)
alpha = 0.05
neg_mean_pinball_loss_05p_scorer = make_scorer(
    mean_pinball_loss,
    alpha=alpha,
    greater_is_better=False,  # maximize the negative loss
)
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, random_state=0)
search_05p = HalvingRandomSearchCV(
    gbr,
    param_grid,
    resource="n_estimators",
    max_resources=250,
    min_resources=50,
    scoring=neg_mean_pinball_loss_05p_scorer,
    n_jobs=2,
    random_state=0,
).fit(X_train, y_train)
pprint(search_05p.best_params_)

{'learning_rate': 0.2,
 'max_depth': 2,
 'min_samples_leaf': 20,
 'min_samples_split': 10,
 'n_estimators': 150}

我们观察到，为中位数回归量手动调整的超参数与适合第5百分位回归量的超参数在相同的范围内。

现在让我们调整第95百分位回归量的超参数。我们需要重新定义 scoring 用于选择最佳模型的指标，并调整内部梯度增强估计器本身的Alpha参数：

from sklearn.base import clone

alpha = 0.95
neg_mean_pinball_loss_95p_scorer = make_scorer(
    mean_pinball_loss,
    alpha=alpha,
    greater_is_better=False,  # maximize the negative loss
)
search_95p = clone(search_05p).set_params(
    estimator__alpha=alpha,
    scoring=neg_mean_pinball_loss_95p_scorer,
)
search_95p.fit(X_train, y_train)
pprint(search_95p.best_params_)

{'learning_rate': 0.05,
 'max_depth': 2,
 'min_samples_leaf': 5,
 'min_samples_split': 20,
 'n_estimators': 150}

结果表明，由搜索过程识别的第95百分位回归量的超参数与中位数回归量的手动调整超参数和由搜索过程识别的第5百分位回归量的超参数大致在相同的范围内。然而，超参数搜索确实导致了90%置信区间的改进，该置信区间由这两个调整的分位数回归量的预测组成。请注意，由于离群值，第95百分位数的预测比第5百分位数的预测具有更粗糙的形状：

y_lower = search_05p.predict(xx)
y_upper = search_95p.predict(xx)

fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.fill_between(
    xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.title("Prediction with tuned hyper-parameters")
plt.show()

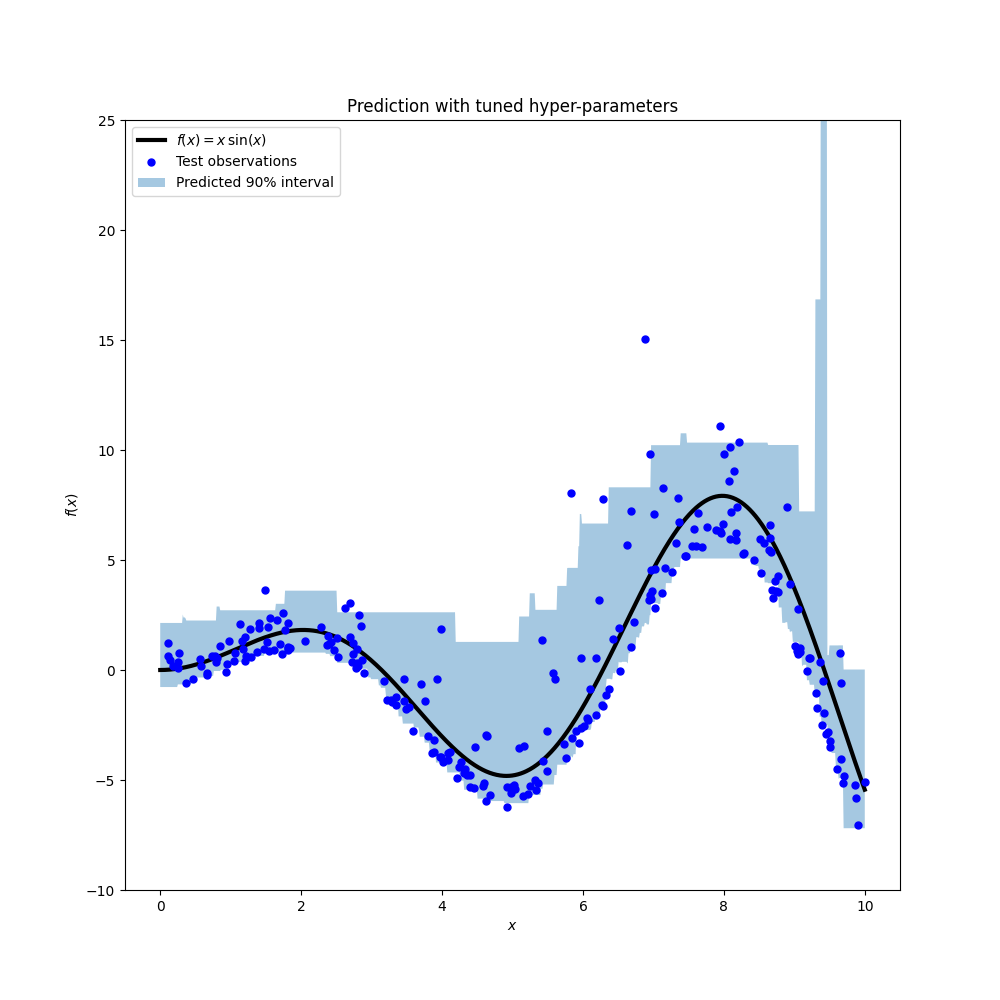
该图在质量上看起来比未经调整的模型更好，尤其是对于较低分位数的形状。

我们现在量化评估这对估计量的联合校准：

coverage_fraction(y_train, search_05p.predict(X_train), search_95p.predict(X_train))

np.float64(0.9026666666666666)

coverage_fraction(y_test, search_05p.predict(X_test), search_95p.predict(X_test))

np.float64(0.796)

不幸的是，在测试集上，调谐对的校准并没有更好：估计的置信区间的宽度仍然太窄。

同样，我们需要将这项研究包裹在交叉验证循环中，以更好地评估这些估计的变异性。

Total running time of the script: （0分10.679秒）