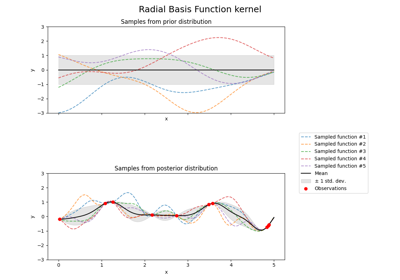
高斯过程回归（GPT）估计数据噪音水平的能力

这个例子展示了 WhiteKernel 以估计数据中的噪音水平。此外，我们还展示了内核超参数初始化的重要性。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

数据生成

我们的工作环境是 X 将包含一个功能。我们创建一个函数来生成要预测的目标。我们将添加一个选项，为生成的目标添加一些噪音。

import numpy as np


def target_generator(X, add_noise=False):
    target = 0.5 + np.sin(3 * X)
    if add_noise:
        rng = np.random.RandomState(1)
        target += rng.normal(0, 0.3, size=target.shape)
    return target.squeeze()

让我们看看目标生成器，其中我们不会添加任何噪音来观察我们想要预测的信号。

X = np.linspace(0, 5, num=80).reshape(-1, 1)
y = target_generator(X, add_noise=False)

import matplotlib.pyplot as plt

plt.plot(X, y, label="Expected signal")
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")

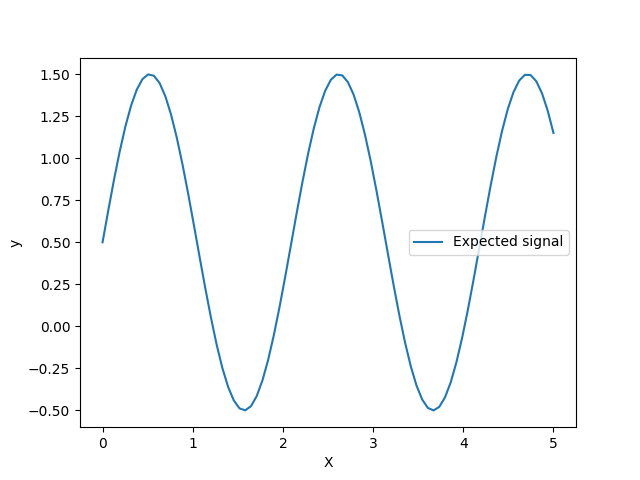
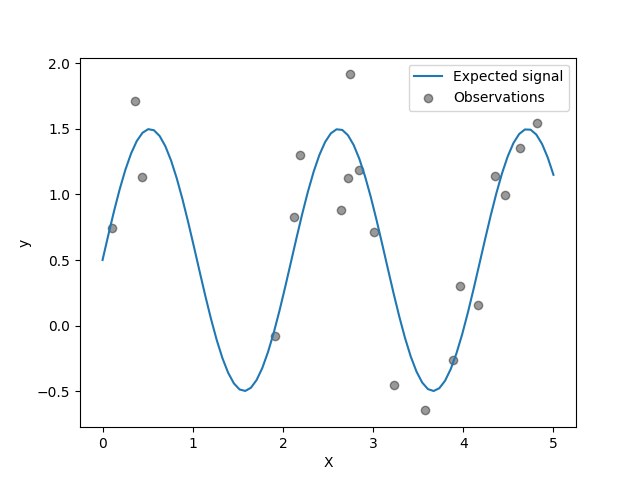
目标是转化输入 X 使用正弦函数。现在，我们将生成一些噪声训练样本。为了说明噪声水平，我们将绘制真实信号和噪声训练样本。

rng = np.random.RandomState(0)
X_train = rng.uniform(0, 5, size=20).reshape(-1, 1)
y_train = target_generator(X_train, add_noise=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(
    x=X_train[:, 0],
    y=y_train,
    color="black",
    alpha=0.4,
    label="Observations",
)
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")

探地雷达中核超参数的优化

现在，我们将创建 GaussianProcessRegressor 使用添加器内核添加 RBF 和 WhiteKernel 果仁。的 WhiteKernel 是一个内核，它将能够估计数据中存在的噪声量， RBF 将用于匹配数据和目标之间的非线性。

然而，我们将证明超参数空间包含几个局部极小值。它将强调初始超参数值的重要性。

我们将使用具有高噪音水平和大长度规模的内核创建一个模型，该模型将通过噪音解释数据中的所有变化。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel

kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

/xpy/lib/python3.11/site-packages/sklearn/gaussian_process/kernels.py:452: ConvergenceWarning:

The optimal value found for dimension 0 of parameter k1__k2__length_scale is close to the specified upper bound 1000.0. Increasing the bound and calling fit again may find a better value.

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

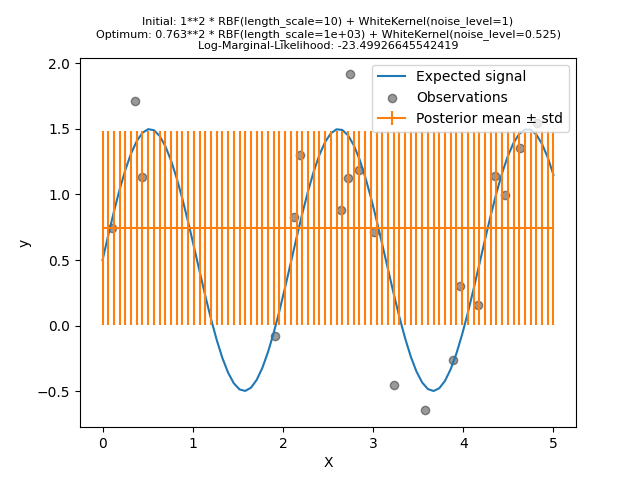
我们看到，找到的最佳内核仍然具有高噪声水平和更大的长度尺度。长度尺度达到了我们允许的这个参数的最大界限，结果我们得到了一个警告。

更重要的是，我们观察到该模型没有提供有用的预测：平均预测似乎是恒定的：它不遵循预期的无噪音信号。

现在，我们将初始化 RBF 具有较大 length_scale 初始值和 WhiteKernel 具有较小的初始噪音水平，同时保持参数界限不变。

kernel = 1.0 * RBF(length_scale=1e-1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1e-2, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

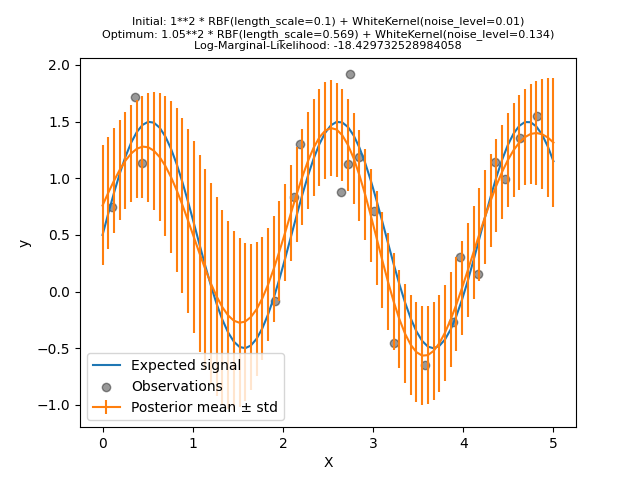
首先，我们看到该模型的预测比之前的模型更精确：这个新模型能够估计无噪音的函数关系。

查看核心超参数，我们发现发现的最佳组合比第一个模型具有更小的噪音水平和更短的长度规模。

我们可以检查的负Log-Marginal-Likemble（LML） GaussianProcessRegressor 对于不同的超参数来了解局部极小值。

from matplotlib.colors import LogNorm

length_scale = np.logspace(-2, 4, num=80)
noise_level = np.logspace(-2, 1, num=80)
length_scale_grid, noise_level_grid = np.meshgrid(length_scale, noise_level)

log_marginal_likelihood = [
    gpr.log_marginal_likelihood(theta=np.log([0.36, scale, noise]))
    for scale, noise in zip(length_scale_grid.ravel(), noise_level_grid.ravel())
]
log_marginal_likelihood = np.reshape(log_marginal_likelihood, noise_level_grid.shape)

vmin, vmax = (-log_marginal_likelihood).min(), 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), num=20), decimals=1)
plt.contour(
    length_scale_grid,
    noise_level_grid,
    -log_marginal_likelihood,
    levels=level,
    norm=LogNorm(vmin=vmin, vmax=vmax),
)
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Length-scale")
plt.ylabel("Noise-level")
plt.title("Negative log-marginal-likelihood")
plt.show()

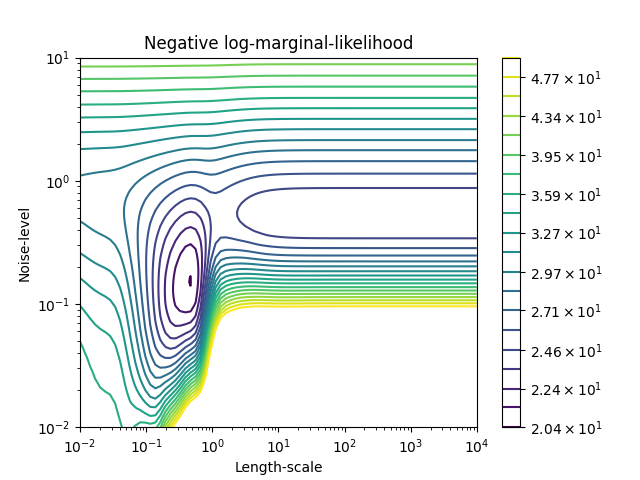
我们看到，有两个局部极小值对应于之前找到的超参数的组合。根据超参数的初始值，基于梯度的优化可能会或可能不会收敛到最佳模型。因此，对于不同的初始化重复优化多次非常重要。这可以通过设置 n_restarts_optimizer 参数 GaussianProcessRegressor 课

让我们再次尝试用坏的初始值来适应我们的模型，但这次随机重新启动10次。

kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
    noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(
    kernel=kernel, alpha=0.0, n_restarts_optimizer=10, random_state=0
)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)

plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
    (
        f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
        f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
    ),
    fontsize=8,
)

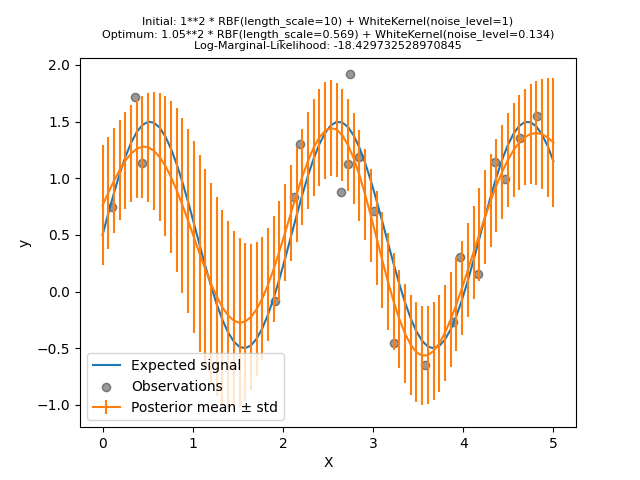
正如我们所希望的那样，随机重启允许优化找到最佳的超参数集，尽管初始值不好。

相关实例

不同核的先验和后验高斯过程的说明

Illustration of prior and posterior Gaussian process for different kernels

高斯过程回归：基本入门示例

Gaussian Processes regression: basic introductory example

利用高斯过程分类（GSK）进行概率预测

Probabilistic predictions with Gaussian process classification (GPC)

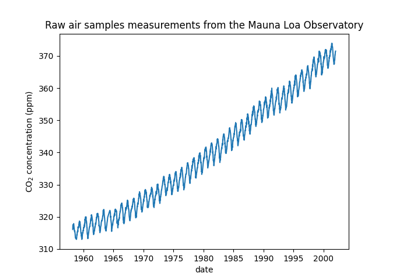
使用高斯过程回归（GPT）预测Mona Loa数据集的二氧化碳水平

Forecasting of CO2 level on Mona Loa dataset using Gaussian process regression (GPR)