多项和一对二回归的决策边界#

此示例比较了具有三个类别的2D数据集上的多项和一对二次逻辑回归的决策边界。

我们对两种方法的决策边界进行比较，相当于调用该方法 predict .此外，当一类的概率估计为0.5时，我们绘制了与该线对应的超平面。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

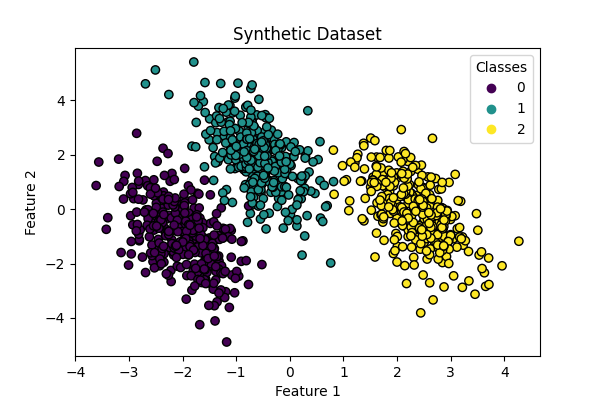
数据集生成#

我们使用生成合成数据集 make_blobs 功能该数据集由来自三个不同类别的1，000个样本组成，以以下为中心 [-5, 0] , [0, 1.5] ，而且 [5, -1] .生成后，我们应用线性变换来引入特征之间的一些相关性，并使问题更具挑战性。这会产生具有三个重叠类别的2D数据集，适合展示多项逻辑回归和一对零回归之间的差异。

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_blobs

centers = [[-5, 0], [0, 1.5], [5, -1]]
X, y = make_blobs(n_samples=1_000, centers=centers, random_state=40)
transformation = [[0.4, 0.2], [-0.4, 1.2]]
X = np.dot(X, transformation)

fig, ax = plt.subplots(figsize=(6, 4))

scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="black")
ax.set(title="Synthetic Dataset", xlabel="Feature 1", ylabel="Feature 2")
_ = ax.legend(*scatter.legend_elements(), title="Classes")

分类器训练#

我们训练两种不同的逻辑回归分类器：多项分类器和一vs-rest分类器。多项分类器同时处理所有类别，而一对休息方法针对所有其他类别训练每个类别的二进制分类器。

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

logistic_regression_multinomial = LogisticRegression().fit(X, y)
logistic_regression_ovr = OneVsRestClassifier(LogisticRegression()).fit(X, y)

accuracy_multinomial = logistic_regression_multinomial.score(X, y)
accuracy_ovr = logistic_regression_ovr.score(X, y)

决策边界可视化#

让我们可视化该方法提供的两个模型的决策边界 predict 分类器的。

from sklearn.inspection import DecisionBoundaryDisplay

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        f"Multinomial Logistic Regression\n(Accuracy: {accuracy_multinomial:.3f})",
        ax1,
    ),
    (
        logistic_regression_ovr,
        f"One-vs-Rest Logistic Regression\n(Accuracy: {accuracy_ovr:.3f})",
        ax2,
    ),
]:
    DecisionBoundaryDisplay.from_estimator(
        model,
        X,
        ax=ax,
        response_method="predict",
        alpha=0.8,
    )
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    legend = ax.legend(*scatter.legend_elements(), title="Classes")
    ax.add_artist(legend)
    ax.set_title(title)

Multinomial Logistic Regression (Accuracy: 0.995), One-vs-Rest Logistic Regression (Accuracy: 0.976)

我们看到决策边界是不同的。这种差异源于他们的做法：

多项逻辑回归在优化期间同时考虑所有类别。
一次与休息的逻辑回归将每个类别独立地与所有其他类别进行匹配。

这些不同的策略可能会导致不同的决策边界，特别是在复杂的多类问题中。

超平面可视化#

当一类的概率估计为0.5时，我们还可视化了与该线对应的超平面。

def plot_hyperplanes(classifier, X, ax):
    xmin, xmax = X[:, 0].min(), X[:, 0].max()
    ymin, ymax = X[:, 1].min(), X[:, 1].max()
    ax.set(xlim=(xmin, xmax), ylim=(ymin, ymax))

    if isinstance(classifier, OneVsRestClassifier):
        coef = np.concatenate([est.coef_ for est in classifier.estimators_])
        intercept = np.concatenate([est.intercept_ for est in classifier.estimators_])
    else:
        coef = classifier.coef_
        intercept = classifier.intercept_

    for i in range(coef.shape[0]):
        w = coef[i]
        a = -w[0] / w[1]
        xx = np.linspace(xmin, xmax)
        yy = a * xx - (intercept[i]) / w[1]
        ax.plot(xx, yy, "--", linewidth=3, label=f"Class {i}")

    return ax.get_legend_handles_labels()

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        "Multinomial Logistic Regression Hyperplanes",
        ax1,
    ),
    (logistic_regression_ovr, "One-vs-Rest Logistic Regression Hyperplanes", ax2),
]:
    hyperplane_handles, hyperplane_labels = plot_hyperplanes(model, X, ax)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    scatter_handles, scatter_labels = scatter.legend_elements()

    all_handles = hyperplane_handles + scatter_handles
    all_labels = hyperplane_labels + scatter_labels

    ax.legend(all_handles, all_labels, title="Classes")
    ax.set_title(title)

plt.show()

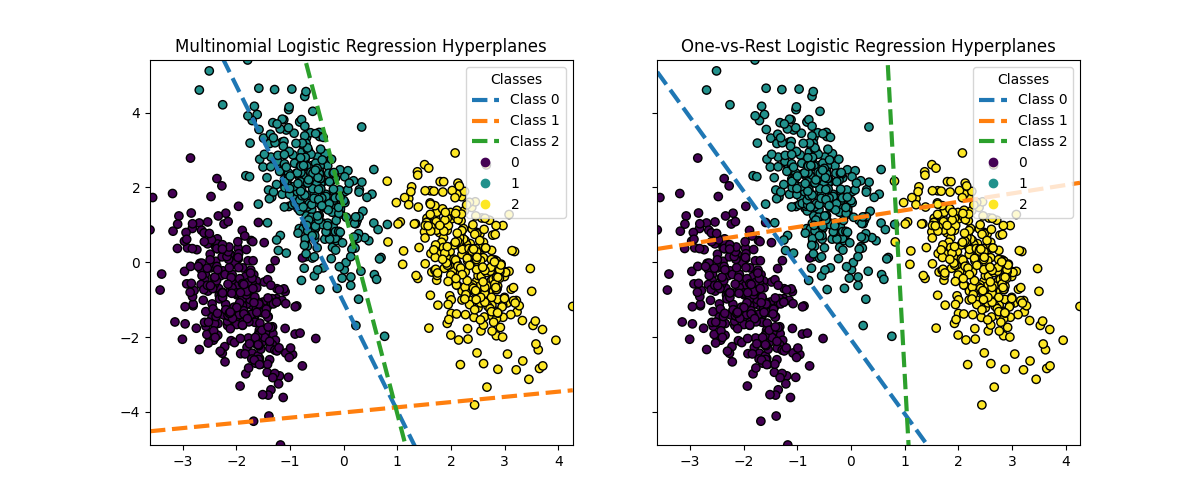
Multinomial Logistic Regression Hyperplanes, One-vs-Rest Logistic Regression Hyperplanes

虽然类0和2的超平面在两种方法之间非常相似，但我们观察到类1的超平面明显不同。这种差异源于one-vs-rest和多项式logistic回归的基本方法：

对于一次与休息的逻辑回归：

每个超平面都是通过考虑一个类与所有其他类来独立确定的。
对于类1，超平面代表最好地将类1与组合的类0和2分开的决策边界。
这种二进制方法可以导致更简单的决策边界，但可能无法同时捕获所有类之间的复杂关系。
条件类概率没有可能的解释。

对于多项逻辑回归：

所有超平面都是同时确定的，同时考虑所有类之间的关系。
模型最小化的损失是适当的评分规则，这意味着模型经过优化以估计条件类概率，因此这些概率是有意义的。
每个超平面代表决策边界，其中一个类别的概率变得高于其他类别，基于总体概率分布。
这种方法可以捕捉类之间更微妙的关系，可能会在多类问题中实现更准确的分类。

超平面的差异，特别是对于第1类，突出了这些方法如何产生不同的决策边界，尽管总体精度相似。

在实践中，建议使用多项逻辑回归，因为它可以最大限度地减少公式良好的损失函数，从而获得更好校准的类概率，从而获得更可解释的结果。当谈到决策边界时，应该制定一个效用函数，将类概率转换为对当前问题有意义的量。One vs-rest允许不同的决策边界，但不允许像效用函数那样对类之间的权衡进行细粒度控制。

Total running time of the script: （0分0.488秒）