具有多项核逼近的可扩展学习#

该实施例说明使用 PolynomialCountSketch 以有效地生成多项核特征空间逼近。这用于训练接近核化分类器准确度的线性分类器。

我们使用Covtype数据集 [2] 在张量素描的原始论文上， [1] ，即由 PolynomialCountSketch .

首先，我们计算线性分类器对原始特征的准确度。然后，我们在不同数量的特征上训练线性分类器 (n_components ）生成于 PolynomialCountSketch ，以可扩展的方式逼近核化分类器的准确性。

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

准备数据#

加载Covype数据集，其中包含581，012个样本，每个样本有54个特征，分布在6个类别中。该数据集的目标是仅根据制图变量（没有遥感数据）预测森林覆盖类型。加载后，我们将其转换为二元分类问题，以匹配LIBSV网页中数据集的版本 [2] ，这是用在 [1] .

from sklearn.datasets import fetch_covtype

X, y = fetch_covtype(return_X_y=True)

y[y != 2] = 0
y[y == 2] = 1  # We will try to separate class 2 from the other 6 classes.

划分数据#

在这里，我们选择5，000个样本进行训练，选择10，000个样本进行测试。要实际重现原始张量草图论文中的结果，请选择100，000进行训练。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=5_000, test_size=10_000, random_state=42
)

特征归一化#

现在将功能扩展到范围 [0, 1] 匹配LIBSV网页中数据集的格式，然后按照原始张量草图论文中所做的标准化为单位长度 [1] .

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler, Normalizer

mm = make_pipeline(MinMaxScaler(), Normalizer())
X_train = mm.fit_transform(X_train)
X_test = mm.transform(X_test)

建立基线模型#

作为基线，根据原始特征训练线性支持机并打印准确性。我们还测量和存储准确性和训练时间，以便稍后绘制它们。

import time

from sklearn.svm import LinearSVC

results = {}

lsvm = LinearSVC()
start = time.time()
lsvm.fit(X_train, y_train)
lsvm_time = time.time() - start
lsvm_score = 100 * lsvm.score(X_test, y_test)

results["LSVM"] = {"time": lsvm_time, "score": lsvm_score}
print(f"Linear SVM score on raw features: {lsvm_score:.2f}%")

Linear SVM score on raw features: 75.62%

建立核逼近模型#

Then we train linear SVMs on the features generated by PolynomialCountSketch with different values for n_components, showing that these kernel feature approximations improve the accuracy of linear classification. In typical application scenarios, n_components should be larger than the number of features in the input representation in order to achieve an improvement with respect to linear classification. As a rule of thumb, the optimum of evaluation score / run time cost is typically achieved at around n_components = 10 * n_features, though this might depend on the specific dataset being handled. Note that, since the original samples have 54 features, the explicit feature map of the polynomial kernel of degree four would have approximately 8.5 million features (precisely, 54^4). Thanks to PolynomialCountSketch, we can condense most of the discriminative information of that feature space into a much more compact representation. While we run the experiment only a single time (n_runs = 1) in this example, in practice one should repeat the experiment several times to compensate for the stochastic nature of PolynomialCountSketch.

from sklearn.kernel_approximation import PolynomialCountSketch

n_runs = 1
N_COMPONENTS = [250, 500, 1000, 2000]

for n_components in N_COMPONENTS:
    ps_lsvm_time = 0
    ps_lsvm_score = 0
    for _ in range(n_runs):
        pipeline = make_pipeline(
            PolynomialCountSketch(n_components=n_components, degree=4),
            LinearSVC(),
        )

        start = time.time()
        pipeline.fit(X_train, y_train)
        ps_lsvm_time += time.time() - start
        ps_lsvm_score += 100 * pipeline.score(X_test, y_test)

    ps_lsvm_time /= n_runs
    ps_lsvm_score /= n_runs

    results[f"LSVM + PS({n_components})"] = {
        "time": ps_lsvm_time,
        "score": ps_lsvm_score,
    }
    print(
        f"Linear SVM score on {n_components} PolynomialCountSketch "
        f"features: {ps_lsvm_score:.2f}%"
    )

Linear SVM score on 250 PolynomialCountSketch features: 76.55%
Linear SVM score on 500 PolynomialCountSketch features: 76.92%
Linear SVM score on 1000 PolynomialCountSketch features: 77.79%
Linear SVM score on 2000 PolynomialCountSketch features: 78.59%

建立核化SVM模型#

训练一个核化的SVM，看看它有多好。 PolynomialCountSketch 接近内核的性能。当然，这可能需要一些时间，因为SRC类的可扩展性相对较差。这就是内核逼近器如此有用的原因：

from sklearn.svm import SVC

ksvm = SVC(C=500.0, kernel="poly", degree=4, coef0=0, gamma=1.0)

start = time.time()
ksvm.fit(X_train, y_train)
ksvm_time = time.time() - start
ksvm_score = 100 * ksvm.score(X_test, y_test)

results["KSVM"] = {"time": ksvm_time, "score": ksvm_score}
print(f"Kernel-SVM score on raw features: {ksvm_score:.2f}%")

Kernel-SVM score on raw features: 79.78%

比较结果#

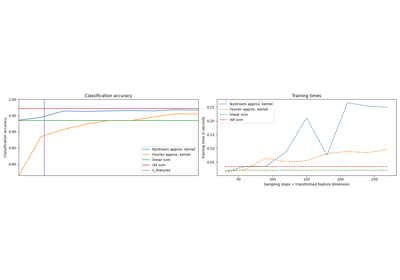
最后，根据训练时间绘制不同方法的结果。正如我们所看到的，核化的支持者实现了更高的准确性，但其训练时间要长得多，最重要的是，如果训练样本数量增加，训练时间会增长得更快。

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(
    [
        results["LSVM"]["time"],
    ],
    [
        results["LSVM"]["score"],
    ],
    label="Linear SVM",
    c="green",
    marker="^",
)

ax.scatter(
    [
        results["LSVM + PS(250)"]["time"],
    ],
    [
        results["LSVM + PS(250)"]["score"],
    ],
    label="Linear SVM + PolynomialCountSketch",
    c="blue",
)

for n_components in N_COMPONENTS:
    ax.scatter(
        [
            results[f"LSVM + PS({n_components})"]["time"],
        ],
        [
            results[f"LSVM + PS({n_components})"]["score"],
        ],
        c="blue",
    )
    ax.annotate(
        f"n_comp.={n_components}",
        (
            results[f"LSVM + PS({n_components})"]["time"],
            results[f"LSVM + PS({n_components})"]["score"],
        ),
        xytext=(-30, 10),
        textcoords="offset pixels",
    )

ax.scatter(
    [
        results["KSVM"]["time"],
    ],
    [
        results["KSVM"]["score"],
    ],
    label="Kernel SVM",
    c="red",
    marker="x",
)

ax.set_xlabel("Training time (s)")
ax.set_ylabel("Accuracy (%)")
ax.legend()
plt.show()

引用#

[1] 范、宁和拉斯穆斯·佩吉。“通过显式特征地图快速且可扩展的多项函数核。“KDD ' 13（2013）。https://doi.org/10.1145/2487575.2487591

[2] LIBSVM二进制数据集存储库https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html

Total running time of the script: （0分15.087秒）