1.6. 最近邻居

sklearn.neighbors 为无监督和有监督的基于邻居的学习方法提供功能。 无监督近邻是许多其他学习方法的基础，尤其是多维学习和谱集群。 受监督的基于邻居的学习有两种类型： classification 对于具有离散标签的数据，以及 regression 对于具有连续标签的数据。

最近邻方法背后的原理是找到距离新点最近的预定义数量的训练样本，并从这些样本中预测标签。 样本的数量可以是用户定义的常数（k-最近邻学习），也可以根据点的局部密度（基于半径的邻居学习）而变化。一般来说，距离可以是任何度量：标准欧几里得距离是最常见的选择。基于邻居的方法称为 non-generalizing 机器学习方法，因为它们简单地“记住”所有的训练数据（可能转换成快速索引结构，如 Ball Tree 或 KD Tree ).

尽管它很简单，但最近邻居在大量分类和回归问题上取得了成功，包括手写数字和卫星图像场景。作为一种非参数方法，它通常在决策边界非常不规则的分类情况下是成功的。

中的类 sklearn.neighbors 可以处理NumPy数组或 scipy.sparse 矩阵作为输入。 对于密集矩阵，支持大量可能的距离度量。 对于稀疏矩阵，搜索支持任意Minkowski度量。

有许多学习例程的核心依赖于最近邻。 一个例子是 kernel density estimation ，在 density estimation 科.

1.6.1. 无人监督的最近邻居

NearestNeighbors 实现无监督的近邻学习。它充当三种不同最近邻算法的统一接口： BallTree , KDTree ，以及基于中例程的暴力算法 sklearn.metrics.pairwise .邻居搜索算法的选择通过关键词控制 'algorithm' ，这必须是 ['auto', 'ball_tree', 'kd_tree', 'brute'] . 当默认值 'auto' 通过时，算法尝试从训练数据中确定最佳方法。 有关每个选项的优点和缺点的讨论，请参阅 Nearest Neighbor Algorithms .

警告

关于最近邻算法，如果两个邻居 \(k+1\) 和 \(k\) 具有相同的距离但不同的标签，结果将取决于训练数据的排序。

1.6.1.1. 寻找最近的邻居

对于寻找两组数据之间最近邻居的简单任务，内部的无监督算法 sklearn.neighbors 可以使用：

>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)
>>> distances
array([[0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356],
       [0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356]])

由于查询集与训练集匹配，因此每个点的最近邻居是距离为零的点本身。

还可以有效地生成显示相邻点之间连接的稀疏图：

>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 1., 1., 0., 0., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 0., 1., 1.]])

数据集的结构使得索引顺序中附近的点在参数空间中附近，从而产生K近邻的大致块对角矩阵。 这种稀疏图在各种情况下都很有用，这些情况利用点之间的空间关系进行无监督学习：特别是，请参阅 Isomap , LocallyLinearEmbedding ，而且 SpectralClustering .

1.6.1.2. KDTree和BallTree课程

或者，可以使用 KDTree 或 BallTree 直接上课寻找最近的邻居。 这是由 NearestNeighbors 上面使用的类。 Ball Tree和KD Tree具有相同的界面;我们将在这里展示使用KD Tree的示例：

>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)

参阅 KDTree 和 BallTree 类文档，了解有关可用于最近邻搜索的选项的更多信息，包括查询策略、距离指标等的规范。有关有效指标使用的列表 KDTree.valid_metrics 和 BallTree.valid_metrics :

>>> from sklearn.neighbors import KDTree, BallTree
>>> KDTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity']
>>> BallTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity', 'seuclidean', 'mahalanobis', 'hamming', 'canberra', 'braycurtis', 'jaccard', 'dice', 'rogerstanimoto', 'russellrao', 'sokalmichener', 'sokalsneath', 'haversine', 'pyfunc']

1.6.2. 最近邻分类

基于邻居的分类是一种 instance-based learning 或 non-generalizing learning 它不试图构建一个通用的内部模型，而只是存储训练数据的实例。分类是根据每个点的最近邻居的简单多数投票来计算的：为查询点分配该点的最近邻居中具有最多代表的数据类。

scikit-learn实现两种不同的最近邻分类器： KNeighborsClassifier 基于 \(k\) 每个查询点的最近邻居，其中 \(k\) 是用户指定的整值。 RadiusNeighborsClassifier 根据固定半径内邻居数量实现学习 \(r\) 每个训练点，其中 \(r\) 是用户指定的浮点值。

的 \(k\) - 邻居分类 KNeighborsClassifier 是最常用的技术。价值的最佳选择 \(k\) 高度依赖数据：一般来说， \(k\) 抑制了噪音的影响，但使分类边界不那么明显。

在数据未均匀采样的情况下，基于半径的邻居分类 RadiusNeighborsClassifier 可以是更好的选择。用户指定固定半径 \(r\) ，以便稀疏邻居中的点使用更少的最近邻居进行分类。 对于多维参数空间，由于所谓的“维度诅咒”，这种方法变得不那么有效。

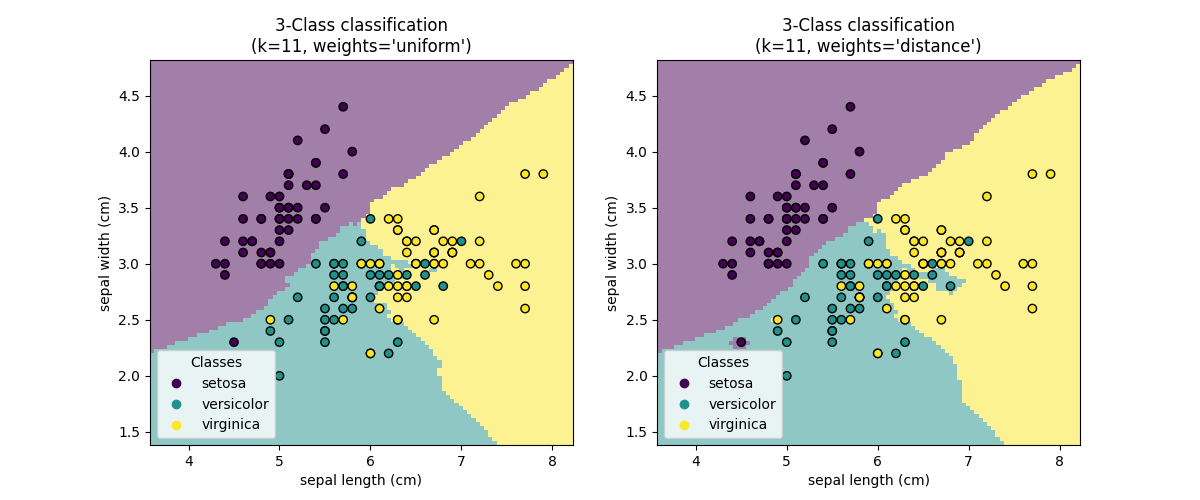
基本的最近邻分类使用统一权重：即，分配给查询点的值是根据最近邻的简单多数投票计算的。 在某些情况下，最好对邻居进行加权，以便更近的邻居对适合度的贡献更大。 这可以通过 weights 关键字 默认值， weights = 'uniform' 为每个邻居分配统一的权重。 weights = 'distance' 分配与距查询点距离的倒数成比例的权重。 或者，可以提供用户定义的距离函数来计算权重。

示例

• 最近邻分类 ：使用最近邻居进行分类的示例。

1.6.3. 最近邻居回归

基于邻居的回归可用于数据标签是连续而不是离散变量的情况。 分配给查询点的标签是根据其最近邻居的标签的平均值计算的。

scikit-learn实现两个不同的邻居回归器： KNeighborsRegressor 基于 \(k\) 每个查询点的最近邻居，其中 \(k\) 是用户指定的整值。 RadiusNeighborsRegressor 实现基于固定半径内邻居的学习 \(r\) 查询点的，其中 \(r\) 是用户指定的浮点值。

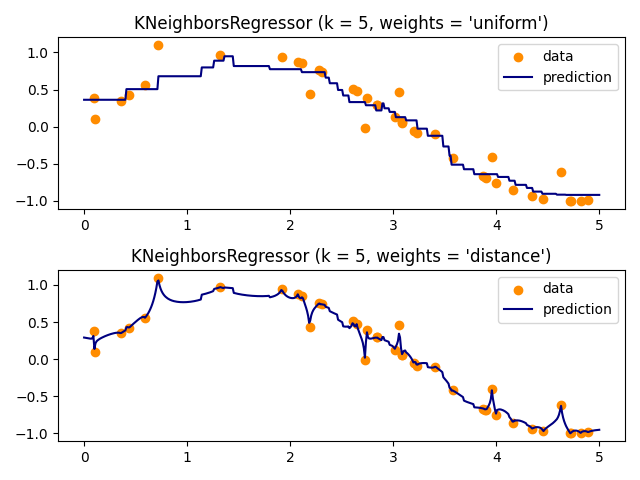
基本的最近邻回归使用统一权重：即，局部邻居中的每个点对查询点的分类都有统一的贡献。 在某些情况下，对点加权可能是有利的，以便附近的点比远处的点对回归的贡献更大。 这可以通过 weights 关键字 默认值， weights = 'uniform' ，为所有点分配相等的权重。 weights = 'distance' 分配与距查询点距离的倒数成比例的权重。或者，可以提供用户定义的距离函数，该函数将用于计算权重。

The use of multi-output nearest neighbors for regression is demonstrated in 使用多输出估计器完成面. In this example, the inputs X are the pixels of the upper half of faces and the outputs Y are the pixels of the lower half of those faces.

示例

• 最近邻回归 ：使用最近邻居的回归示例。

• 使用多输出估计器完成面 ：使用最近邻居的多输出回归的示例。

1.6.4. 最近邻居算法

1.6.4.1. 蛮力

最近邻的快速计算是机器学习的一个活跃研究领域。最简单的邻居搜索实现涉及数据集中所有点对之间距离的暴力计算： \(N\) 样品 \(D\) 维度，这种方法的规模为 \(O[D N^2]\) . 高效的暴力邻居搜索对于小数据样本来说非常有竞争力。然而，随着样本数量 \(N\) 随着时间的增长，暴力方法很快就会变得不可行。 在里面的班级里 sklearn.neighbors ，使用关键字指定暴力邻居搜索 algorithm = 'brute' ，并使用中可用的例程计算 sklearn.metrics.pairwise .

1.6.4.2. K-D树

为了解决暴力方法的计算效率低下的问题，人们发明了各种基于树的数据结构。 一般来说，这些结构试图通过有效地编码样本的聚合距离信息来减少所需的距离计算数量。基本想法是如果点 \(A\) 与点非常遥远 \(B\) ，和点 \(B\) 非常接近点 \(C\) ，那么我们就知道了点 \(A\) 和 \(C\) 距离很远， without having to explicitly calculate their distance .这样，最近邻搜索的计算成本可以降低到 \(O[D N \log(N)]\) 或者更好。这是对大规模暴力的重大改进 \(N\) .

An early approach to taking advantage of this aggregate information was the KD tree data structure (short for K-dimensional tree), which generalizes two-dimensional Quad-trees and 3-dimensional Oct-trees to an arbitrary number of dimensions. The KD tree is a binary tree structure which recursively partitions the parameter space along the data axes, dividing it into nested orthotropic regions into which data points are filed. The construction of a KD tree is very fast: because partitioning is performed only along the data axes, no \(D\)-dimensional distances need to be computed. Once constructed, the nearest neighbor of a query point can be determined with only \(O[\log(N)]\) distance computations. Though the KD tree approach is very fast for low-dimensional (\(D < 20\)) neighbors searches, it becomes inefficient as \(D\) grows very large: this is one manifestation of the so-called "curse of dimensionality". In scikit-learn, KD tree neighbors searches are specified using the keyword algorithm = 'kd_tree', and are computed using the class KDTree.

引用

• "Multidimensional binary search trees used for associative searching" <https://dl.acm.org/citation.cfm?doid=361002.361007> _，Bentley，J.L.，ACM通讯（1975年）

1.6.4.3. Ball Tree

为了解决更高维度KD树的低效问题， ball tree 数据结构已开发。 KD树沿着笛卡儿轴划分数据，而球树则在一系列嵌套超球体中划分数据。 这使得树的构建比KD树的成本更高，但产生的数据结构在高度结构化的数据上非常有效，即使是在非常高的维度上。

球树将数据递进地划分为由重心定义的节点 \(C\) 和半径 \(r\) ，使得节点中的每个点都位于由 \(r\) 和 \(C\) .通过使用 triangle inequality :

\[|x+y| \leq |x| + |y|\]

通过这种设置，测试点和重心之间的单一距离计算足以确定到节点内所有点的距离的下限和上限。由于球树节点的球形几何形状，它的性能优于 KD-tree 在高维度中，尽管实际性能高度依赖于训练数据的结构。在scikit-learn中，使用关键字指定基于球树的邻居搜索 algorithm = 'ball_tree' ，并使用类计算 BallTree .或者，用户可以使用 BallTree 直接上课。

引用

• "Five Balltree Construction Algorithms" <https://citeseerx.ist.psu.edu/doc_view/pid/17ac002939f8e950ffb32ec4dc8e86bdd8cb5ff1> _，Omohundro，SM，国际计算机科学研究所技术报告（1989年）

最近邻居选择算法

给定数据集的最佳算法是一个复杂的选择，并且取决于多种因素：

• 数量的样本 \(N\) （即 n_samples ）和维度 \(D\) （即 n_features ).

  • Brute force 查询时间随着 \(O[D N]\)

  • Ball tree 查询时间增长大约 \(O[D \log(N)]\)

  • KD tree 查询时间随着 \(D\) 以一种难以精确量化的方式。 小 \(D\) (less超过20左右）成本大约是 \(O[D\log(N)]\) ，并且KD树查询可以非常高效。对于较大 \(D\) ，成本增加到近 \(O[DN]\) ，并且树结构造成的负担可能会导致查询比暴力更慢。

  对于小数据集 (\(N\) 少于30个左右）， \(\log(N)\) 堪比 \(N\) ，并且暴力算法可能比基于树的方法更有效。 两 KDTree 和 BallTree 通过提供 leaf size 参数：这控制查询切换到暴力时的样本数。 这使得这两种算法都接近小型的暴力计算的效率 \(N\) .

• 数据结构： intrinsic dimensionality 数据和/或 sparsity 的数据。内在维度是指维度 \(d \le D\) 数据所在的多管齐下，它可以线性或非线性嵌入参数空间中。稀疏性是指数据填充参数空间的程度（这与“稀疏”矩阵中使用的概念区分开来。 数据矩阵可能没有零项，但 structure 在这个意义上仍然可以是“稀疏的”）。

  • Brute force 查询时间不受数据结构的影响。

  • Ball tree 和 KD tree 查询时间可能会受到数据结构的很大影响。 一般来说，内在维度较小的稀疏数据会导致更快的查询时间。 由于KD树内部表示与参数轴对齐，因此对于任意结构化的数据，它通常不会表现出像球树那么多的改进。

  机器学习中使用的数据集往往非常结构化，非常适合基于树的查询。

• 相邻要素的数目 \(k\) 请求查询点。

  • Brute force 查询时间在很大程度上不受 \(k\)

  • Ball tree 和 KD tree 查询时间将变得更慢， \(k\) 增大 这是由于两个影响：首先，更大的 \(k\) 导致需要搜索参数空间的更大部分。二是利用 \(k > 1\) 在穿越树时需要对结果进行内部排队。

  作为 \(k\) 与之相比， \(N\) ，在基于树的查询中修剪分支的能力就会降低。 在这种情况下，粗暴查询可以更有效。

• 查询点的数量。 球树和KD树都需要一个构建阶段。 当在许多查询中摊销时，该建设的成本变得可以忽略不计。 然而，如果只执行少量查询，则构建可能会占总成本的很大一部分。 如果需要很少的查询点，那么暴力比基于树的方法更好。

目前， algorithm = 'auto' 选择 'brute' 如果验证以下任何情况：

• 输入数据稀疏

• metric = 'precomputed'

• \(D > 15\)

• \(k >= N/2\)

• effective_metric_ 中没有 VALID_METRICS 任何一个的列表 'kd_tree' 或 'ball_tree'

否则，它会选择第一个 'kd_tree' 和 'ball_tree' 具有 effective_metric_ 在其 VALID_METRICS 名单该启发式基于以下假设：

• 查询点的数量至少与训练点的数量顺序相同

• leaf_size 接近其默认值 30

• 当 \(D > 15\) ，对于基于树的方法来说，数据的内在维度通常太高

的影响 leaf_size

如上所述，对于小样本大小，暴力搜索可能比基于树的查询更有效。 通过内部切换到叶节点内的暴力搜索，在球树和KD树中考虑了这一事实。 此开关的级别可以使用参数指定 leaf_size . 此参数选择有很多影响：

construction time

更大的 leaf_size 导致树构建时间更快，因为需要创建的节点更少

query time

无论是大还是小 leaf_size 可能导致次优的查询成本。为 leaf_size 接近1时，穿越节点涉及的负载可能会显着减慢查询时间。 为 leaf_size 接近训练集的大小时，查询本质上变成了暴力。两者之间的一个很好的妥协是 leaf_size = 30 ，参数的默认值。

memory

作为 leaf_size 增加时，存储树结构所需的内存就会减少。 这对于球树来说尤其重要，它存储了 \(D\) - 每个节点的维度重心。 所需的存储空间 BallTree 约为 1 / leaf_size 乘以训练集的大小。

leaf_size 未被引用用于强力查询。

最近邻算法的有效收件箱

有关可用指标的列表，请参阅 DistanceMetric 类和中列出的指标 sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS .请注意，“cos”指标使用 cosine_distances .

A list of valid metrics for any of the above algorithms can be obtained by using their valid_metric attribute. For example, valid metrics for KDTree can be generated by:

>>> from sklearn.neighbors import KDTree
>>> print(sorted(KDTree.valid_metrics))
['chebyshev', 'cityblock', 'euclidean', 'infinity', 'l1', 'l2', 'manhattan', 'minkowski', 'p']

1.6.5. 最近的重心分类器

的 NearestCentroid 分类器是一种简单的算法，通过其成员的重心来表示每个类别。实际上，这使得它类似于 KMeans 算法它也没有可选择的参数，使其成为一个很好的基线分类器。然而，它确实会在非凸类上受到影响，以及当类具有巨大方差差异时，因为假设所有维度的方差相等。请参阅线性辨别分析 (LinearDiscriminantAnalysis ）和二次鉴别分析 (QuadraticDiscriminantAnalysis ）对于不做出这一假设的更复杂的方法。默认值的使用 NearestCentroid 很简单：

>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]

1.6.5.1. 最近的缩小的中心

的 NearestCentroid 分类器具有 shrink_threshold 参数，它实现了最近的收缩质心分类器。实际上，每个质心的每个特征的值除以该特征的类内方差。然后，特征值被减少， shrink_threshold .最值得注意的是，如果特定特征值过零，则将其设置为零。实际上，这消除了该特征对分类的影响。例如，这对于去除有噪的特征很有用。

在下面的示例中，使用较小的收缩阈值可以将模型的准确性从0.81提高到0.82。

最近的中心_1最近的中心_2

示例

• 最近的重心分类 ：使用具有不同收缩阈值的最近重心进行分类的示例。

1.6.6. 最近邻Transformer

许多scikit-learning估计器依赖于最近的邻居：几个分类器和回归器，例如 KNeighborsClassifier 和 KNeighborsRegressor ，还有一些集群方法，例如 DBSCAN 和 SpectralClustering ，以及一些多种嵌入，例如 TSNE 和 Isomap .

所有这些估计器都可以在内部计算最近邻居，但其中大多数也接受预先计算的最近邻居 sparse graph ，如由 kneighbors_graph 和 radius_neighbors_graph .具有模式 mode='connectivity' ，这些函数根据需要返回二进制邻近稀疏图，例如， SpectralClustering .而对于 mode='distance' ，它们根据需要返回距离稀疏图，例如， DBSCAN .要将这些函数包含在scikit-learn管道中，还可以使用相应的类 KNeighborsTransformer 和 RadiusNeighborsTransformer .这个稀疏图API的好处是多方面的。

First, the precomputed graph can be reused multiple times, for instance while varying a parameter of the estimator. This can be done manually by the user, or using the caching properties of the scikit-learn pipeline:

>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir()  # we use a temporary folder here
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
...     KNeighborsTransformer(mode='distance'),
...     Isomap(n_components=3, metric='precomputed'),
...     memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)

其次，预先计算图可以对最近邻估计进行更精细的控制，例如通过参数启用多处理 n_jobs ，这可能并非在所有估计器中都可用。

最后，预计算可以由自定义估计器执行，以使用不同的实现，例如近似最近邻方法，或具有特殊数据类型的实现。预先计算的邻居 sparse graph 需要格式化为中 radius_neighbors_graph 输出：

• CSR矩阵（尽管将接受COO、CSC或LIL）。

• 仅显式存储每个样本相对于训练数据的最近邻居。这应该包括与查询点距离为0的那些，包括计算训练数据与其本身之间最近的邻居时的矩阵对角线。

• 每一行的 data 应按递减顺序存储距离（可选。未排序的数据将被稳定排序，从而增加计算负担）。

• 数据中的所有值都应该是非负的。

• 不应该有重复的 indices 在任何行中（参见https：//github.com/scipy/scipy/issues/5807）。

• 如果传递预先计算的矩阵的算法使用k个最近的邻居（与半径邻居相反），则必须在每一行中存储至少k个邻居（或k+1，如以下注释中所解释的）。

备注

当查询特定数量的邻居时（使用 KNeighborsTransformer ），的定义 n_neighbors 是模糊的，因为它可以将每个训练点包括为其自己的邻居，也可以将它们排除在外。这两种选择都不是完美的，因为将它们纳入训练和测试期间会导致非我邻居数量的不同，而将它们排除在外会导致非我邻居数量的不同 fit(X).transform(X) 和 fit_transform(X) ，这是针对scikit-learn API的。在 KNeighborsTransformer 我们使用的定义包括每个训练点作为它自己的邻居在计数 n_neighbors .然而，出于与使用其他定义的其他估计器的兼容性原因，当 mode == 'distance' .为了最大化与所有估计器的兼容性，一个安全的选择是始终在自定义最近邻估计器中包括一个额外的邻居，因为不必要的邻居将被以下估计器过滤。

示例

• TSNE的大约最近邻居 ：管道化的一个例子 KNeighborsTransformer 和 TSNE .还提出了两个基于外部包的自定义最近邻估计器。

• 缓存最近的邻居 ：管道化的一个例子 KNeighborsTransformer 和 KNeighborsClassifier 以在超参数网格搜索期间启用邻居图的缓存。

1.6.7. 邻里要素分析

邻里要素分析（NCA， NeighborhoodComponentsAnalysis ）是一种距离度量学习算法，其目的是与标准欧几里得距离相比提高最近邻分类的准确性。该算法直接最大化训练集上的留一法k近邻（KNN）得分的随机变量。它还可以学习数据的低维线性投影，可用于数据可视化和快速分类。

nca_adfertion_1 nca_adfertion_2

在上面的插图中，我们考虑了随机生成的数据集中的一些点。我们重点关注点3的随机KNN分类。样本3和另一个点之间链接的厚度与它们的距离成正比，并且可以被视为随机最近邻预测规则分配给该点的相对权重（或概率）。在原始空间中，样本3有许多来自各个类的随机邻居，因此正确的类不太可能。然而，在NCA学习的投影空间中，唯一具有不可忽略权重的随机邻居来自与样本3相同的类，确保后者将被很好地分类。看到 mathematical formulation 了解更多详细信息。

1.6.7.1. 分类

结合最近邻分类器 (KNeighborsClassifier ），NCA对于分类来说很有吸引力，因为它可以自然地处理多类问题，而无需增加模型大小，并且不会引入需要用户微调的额外参数。

NCA分类已被证明在实践中对于不同大小和难度的数据集效果良好。与线性鉴别分析等相关方法不同，NCA不对类别分布做出任何假设。最近邻分类自然会产生高度不规则的决策边界。

要使用此模型进行分类，需要结合 NeighborhoodComponentsAnalysis 学习最佳转换的实例 KNeighborsClassifier 在投影空间中执行分类的实例。以下是使用这两个类的示例：

>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...

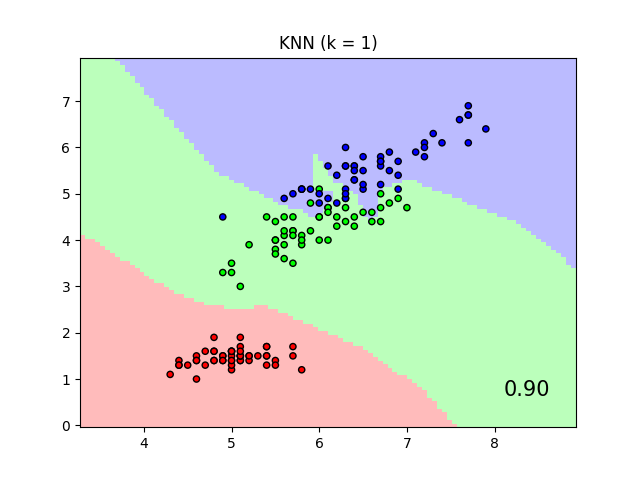
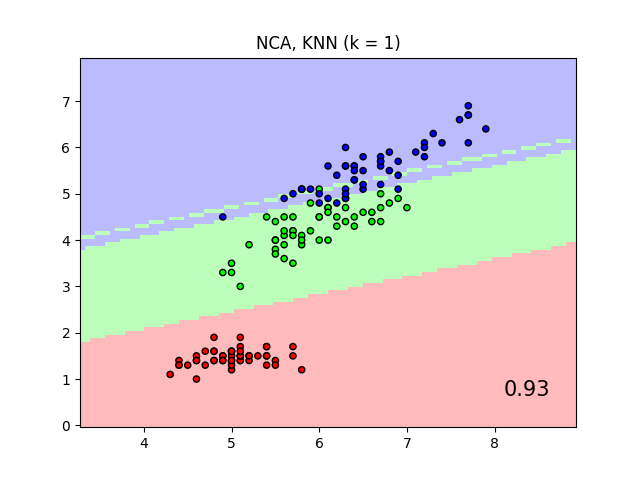
出于可视化目的，该图显示了仅对两个特征进行训练和评分时，虹膜数据集上的最近邻分类和邻居成分分析分类的决策边界。

1.6.7.2. 降维

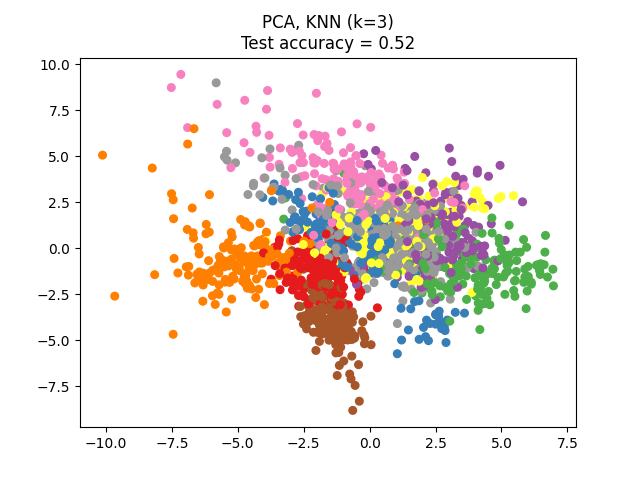
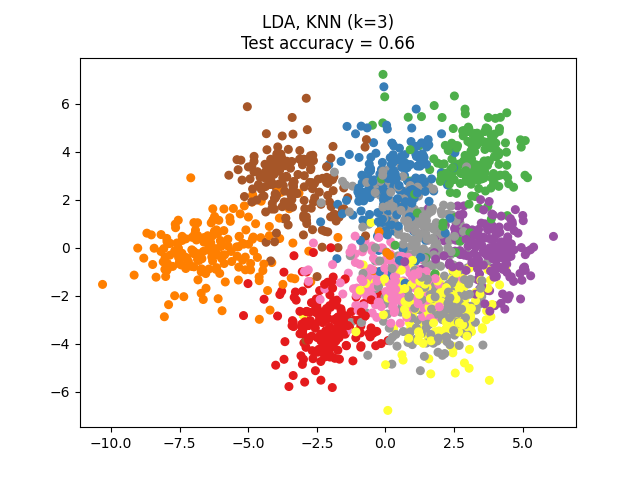
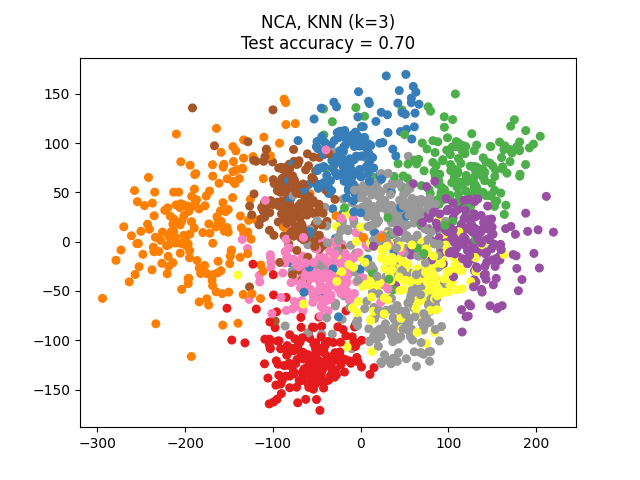
NCA可用于执行监督降维。将输入数据投影到由最小化NCA目标的方向组成的线性子空间上。可以使用参数设置所需的维数 n_components .例如，下图显示了降维与主成分分析的比较 (PCA ）、线性鉴别分析 (LinearDiscriminantAnalysis ）和邻里成分分析 (NeighborhoodComponentsAnalysis ）在Digits数据集上，一个有大小的数据集 \(n_{samples} = 1797\) 和 \(n_{features} = 64\) .数据集被分成相等大小的训练集和测试集，然后标准化。为了评估3-最近邻分类精度计算的2维投影点发现的每种方法。每个数据样本属于10个类之一。

示例

• 比较使用和不使用邻居成分分析的最近邻居

• 利用邻居成分分析降低维度

• 手写数字的流形学习：局部线性嵌入，Isomap...

1.6.7.3. 数学公式

NCA的目标是学习大小的最佳线性变换矩阵 (n_components, n_features) ，它使所有样本的总和最大化 \(i\) 概率 \(p_i\) 的 \(i\) 已正确分类，即：

\[\underset{L}{\arg\max} \sum\limits_{i=0}^{N - 1} p_{i}\]

与 \(N\) = n_samples 和 \(p_i\) 样本的概率 \(i\) 根据所学习的嵌入空间中的随机最近邻规则正确分类：

\[p_{i}=\sum\limits_{j \in C_i}{p_{i j}}\]

哪里 \(C_i\) 是与样本相同类中的点集 \(i\) ，而且 \(p_{i j}\) 是嵌入空间中欧几里得距离上的softmax：

\[p_{i j} = \frac{\exp(-||L x_i - L x_j||^2)}{\sum\limits_{k \ne i} {\exp{-(||L x_i - L x_k||^2)}}} , \quad p_{i i} = 0\]

马氏距离

NCA可以被视为学习（平方）Mahalanobis距离指标：

\[|| L（x_i - x_j）||' 2 =（x_i - x_j）' TM（x_i - x_j），\]

哪里 \(M = L^T L\) 是一个对称的正半定大小矩阵 (n_features, n_features) .

1.6.7.4. 执行

此实现遵循原始论文中解释的内容 [1]. 对于优化方法，它目前使用scipy的L-BFSG-B，在每次迭代时进行完整的梯度计算，以避免调整学习率并提供稳定的学习。

请参阅下面的示例和 NeighborhoodComponentsAnalysis.fit 获取更多信息.

1.6.7.5. 复杂性

1.6.7.5.1. 培训

NCA存储成对距离矩阵，取 n_samples ** 2 记忆时间复杂性取决于优化算法执行的迭代次数。然而，可以使用参数设置最大迭代次数 max_iter .对于每次迭代，时间复杂性是 O(n_components x n_samples x min(n_samples, n_features)) .

1.6.7.5.2. 变换

这里 transform 操作返回 \(LX^T\) ，因此其时间复杂度等于 n_components * n_features * n_samples_test .操作中不会增加空间复杂性。

引用

[1]

"Neighbourhood Components Analysis" <https://papers.nips.cc/paper_files/paper/2004/file/42fe880812925e520249e808937738d2-Paper.pdf> _，J·戈德堡，S. Roweis，G.辛顿河Salakhutdinov，《神经信息处理系统的进展》，第17卷，2005年5月，第17页。513-520.

• Wikipedia entry on Neighborhood Components Analysis <https://en.wikipedia.org/wiki/Neighbourhood_components_analysis> _