7.7. 核近似

该子模块包含近似对应于某些内核的特征映射的函数，因为它们用于例如支持向量机（参见 支持向量机 ).以下特征函数对输入执行非线性变换，这可以作为线性分类或其他算法的基础。

与使用大致显式特征地图相比，使用大致显式特征地图的优势 kernel trick 隐式利用特征地图的原因是显式映射可以更适合在线学习，并且可以显着降低使用非常大的数据集的学习成本。标准的内核化支持器不能很好地扩展到大型数据集，但使用大约的内核映射，可以使用效率更高的线性支持器。特别是，核地图逼近与 SGDClassifier 可以使大型数据集上的非线性学习成为可能。

由于使用近似嵌入的经验工作并不多，因此建议尽可能将结果与精确的内核方法进行比较。

参见

多元回归：用基函数扩展线性模型 进行精确的多项变换。

7.7.1. 核逼近的Nystroem方法

The Nystroem method, as implemented in Nystroem is a general method for reduced rank approximations of kernels. It achieves this by subsampling without replacement rows/columns of the data on which the kernel is evaluated. While the computational complexity of the exact method is \(\mathcal{O}(n^3_{\text{samples}})\), the complexity of the approximation is \(\mathcal{O}(n^2_{\text{components}} \cdot n_{\text{samples}})\), where one can set \(n_{\text{components}} \ll n_{\text{samples}}\) without a significant decrease in performance [WS2001].

我们可以构造核矩阵的特征分解 \(K\) ，根据数据的特征，然后将其拆分为采样和未采样的数据点。

\[\begin{split}K = U \Lambda U^T = \begin{bmatrix} U_1 \\ U_2\end{bmatrix} \Lambda \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}^T = \begin{bmatrix} U_1 \Lambda U_1^T & U_1 \Lambda U_2^T \\ U_2 \Lambda U_1^T & U_2 \Lambda U_2^T \end{bmatrix} \equiv \begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix}\end{split}\]

其中：

• \(U\) 是正常的

• \(\Lambda\) 是特征值的对角矩阵

• \(U_1\) 是所选样本的标准正交矩阵

• \(U_2\) 是未选择的样本的标准正交矩阵

鉴于 \(U_1 \Lambda U_1^T\) 可以通过矩阵的正交化获得 \(K_{11}\) ，而且 \(U_2 \Lambda U_1^T\) 可以被评估（以及它的转置），唯一剩下需要阐明的术语是 \(U_2 \Lambda U_2^T\) .为此，我们可以用已经评估过的矩阵来表达它：

\[\begin{split}\begin{align} U_2 \Lambda U_2^T &= \left(K_{21} U_1 \Lambda^{-1}\right) \Lambda \left(K_{21} U_1 \Lambda^{-1}\right)^T \\&= K_{21} U_1 (\Lambda^{-1} \Lambda) \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} U_1 \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} K_{11}^{-1} K_{21}^T \\&= \left( K_{21} K_{11}^{-\frac12} \right) \left( K_{21} K_{11}^{-\frac12} \right)^T .\end{align}\end{split}\]

期间 fit ，班级 Nystroem 评估基础 \(U_1\) ，并计算正规化常数， \(K_{11}^{-\frac12}\) .后来到 transform ，核矩阵是在基（由 components_ 属性）和新的数据点， X .然后将此矩阵乘以 normalization_ 最终结果的矩阵。

默认情况下 Nystroem 使用 rbf 内核，但它可以使用任何内核函数或预先计算的内核矩阵。使用的样本数量（也是计算出的特征的维度）由参数给出 n_components .

示例

• 请参阅标题为的示例 与时间相关的特征工程 ，这展示了一个使用 Nystroem 内核。

7.7.2. 放射基函数核

的 RBFSampler 为辐射基函数核构建一个近似映射，也称为 Random Kitchen Sinks [RR2007]. 在应用线性算法之前，该转换可以用于显式地建模核映射：：

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

该映射依赖于对内核值的蒙特卡罗近似。的 fit 函数执行Monte Carlo采样，而 transform 方法执行数据的映射。 由于过程固有的随机性，不同调用的结果可能会有所不同 fit 功能

的 fit 函数接受两个参数： n_components ，其是特征变换的目标维度，以及 gamma ，RBF内核的参数。 更高 n_components 将产生更好的核逼近，并产生与核支持机产生的结果更相似的结果。请注意，“匹配”特征函数实际上并不取决于提供给 fit 功能仅使用数据的维度。有关该方法的详细信息请参阅 [RR2007].

对于给定值的 n_components RBFSampler 通常不太准确， Nystroem . RBFSampler 不过，计算成本更低，从而更有效地利用更大的特征空间。

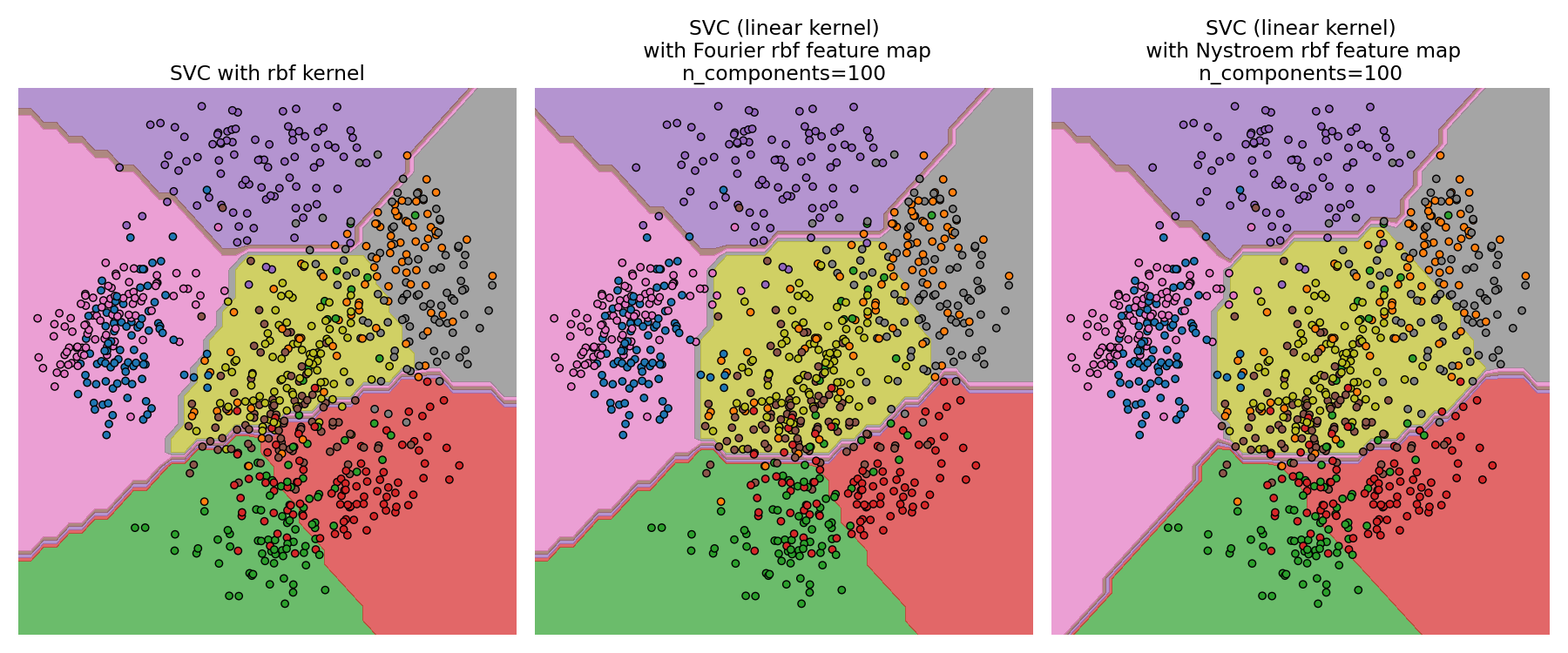
比较精确的RBS核（左）与逼近核（右）

示例

• 基于RBS核的显式特征图逼近

7.7.3. 加性卡平方核

加性卡平方核是柱状图的一个核，通常用于计算机视觉。

这里使用的加性卡平方核由下式给出

\[k（x，y）= \sum_i \fRAC{2x_iy_i}{x_i+y_i}\]

这与 sklearn.metrics.pairwise.additive_chi2_kernel .的作者 [VZ2010] 更喜欢上面的版本，因为它总是肯定的。由于内核是可添加的，因此可以处理所有成分 \(x_i\) 单独用于嵌入。这使得可以以规则的间隔对傅里叶变换进行采样，而不是使用蒙特卡洛采样进行逼近。

类 AdditiveChi2Sampler 实现这种组件式确定性采样。每个组件都进行抽样 \(n\) 时代，屈服 \(2n+1\) 每个输入维度的维度（二的倍数源于傅里叶变换的实部分和复部分）。在文献中， \(n\) 通常选择为1或2，将数据集转换为大小 n_samples * 5 * n_features (in的情况 \(n=2\) ).

由提供的大致特征地图 AdditiveChi2Sampler 可以与提供的近似特征图相结合， RBFSampler 以产生取指数的卡平方核的大约特征地图。看到 [VZ2010] 有关详细信息和 [VVZ2010] 用于与 RBFSampler .

7.7.4. 斜方核

斜卡平方核由下式给出：

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

它的属性与计算机视觉中经常使用的取指数卡平方核类似，但允许对特征地图进行简单的蒙特卡罗逼近。

的使用 SkewedChi2Sampler 与上述的使用相同 RBFSampler .唯一的区别是自由参数，即所谓的 \(c\) .有关此映射的动机和数学细节，请参阅 [LS2010].

7.7.5. 通过张量草图进行多项核逼近

的 polynomial kernel 是一种流行的内核函数类型，由以下公式给出：

\[k（x，y）=（\gamma x^\top y +c_0）' d\]

其中：

• x , y 是输入载体

• d 是核心度

直观地说，次数的多项核的特征空间 d 由输入特征之间所有可能的度' d '积组成，这使得学习算法能够使用此内核来考虑特征之间的交互。

张量草图 [PP2013] 方法，如在中实现的 PolynomialCountSketch ，是一种可扩展的、独立于输入数据的多项核逼近方法。它基于伯爵素描的概念 [WIKICS] [CCF2002] ，一种类似于特征哈希的维度缩减技术，而是使用几个独立的哈希函数。TensorSketch获得两个载体（或一个载体与其本身）的外积的计数Sketch，它可以用作多元核特征空间的逼近。特别是，TensorSketch不是显式计算外积，而是计算载体的计数草图，然后通过快速傅里叶变换使用多项相乘来计算其外积的计数草图。

Conveniently, the training phase of TensorSketch simply consists of initializing some random variables. It is thus independent of the input data, i.e. it only depends on the number of input features, but not the data values. In addition, this method can transform samples in \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\) time, where \(n_{\text{components}}\) is the desired output dimension, determined by n_components.

示例

• 具有多项核逼近的可扩展学习

7.7.6. 数学细节

支持向量机或核化PCA等核方法依赖于复制核希尔伯特空间的性质。对于任何正值核函数 \(k\) （所谓的Mercer内核），保证存在映射 \(\phi\) 希尔伯特空间 \(\mathcal{H}\) ，这样

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

Where \(\langle \cdot, \cdot \rangle\) denotes the inner product in the Hilbert space.

如果线性支持向量机或PCA等算法仅依赖于数据点的纯积 \(x_i\) ，可以使用的值 \(k(x_i, x_j)\) ，相当于将算法应用于映射的数据点 \(\phi(x_i)\) .的好处 \(k\) 是地图 \(\phi\) 永远不必显式计算，从而允许任意大特征（甚至无限大）。

内核方法的一个缺点是，可能需要存储许多内核值 \(k(x_i, x_j)\) 优化期间。如果将核化分类器应用于新数据 \(y_j\) , \(k(x_i, y_j)\) 需要计算才能做出预测，可能针对许多不同的 \(x_i\) 在训练集中。

此子模块中的类允许逼近嵌入 \(\phi\) ，从而显式地与表示一起工作 \(\phi(x_i)\) ，这消除了应用内核或存储训练示例的需要。

引用

[WS2001]

"Using the Nyström method to speed up kernel machines" 威廉姆斯，CKI;西格，M. - 2001.

[RR2007] (1,2)

"Random features for large-scale kernel machines" 拉希米，A.和Recht，B. - 神经信息处理进展2007年，

[LS2010]

"Random Fourier approximations for skewed multiplicative histogram kernels" 李，F.，约内斯库，C.，和斯明奇塞斯库，C. - 模式识别，DAGM 2010，计算机科学讲座笔记。

[VZ2010] (1,2)

"Efficient additive kernels via explicit feature maps" 维达尔迪，A.和Zisserman，A. - 计算机视觉与模式识别2010

[VVZ2010]

"Generalized RBF feature maps for Efficient Detection" 文帕蒂，S.和维达尔迪，A.和Zisserman，A.和Jawahar，CV - 2010

[PP2013]

"Fast and scalable polynomial kernels via explicit feature maps" 范，N.，' Pagh，R. - 2013

[CCF2002]

"Finding frequent items in data streams" 查里卡，M.，陈，K.，& Farach-Colton - 2002

[WIKICS]

"Wikipedia: Count sketch" <https://en.wikipedia.org/wiki/Count_sketch> _