2.4. 双聚类#

双集群算法同时对数据矩阵的行和列进行集群。这些行和列的集群被称为双集群。每个都确定具有某些所需属性的原始数据矩阵的子矩阵。

例如，给定形状矩阵 (10, 10) ，一个可能的具有三行两列的双集群会产生形状的子矩阵 (3, 2)

>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

为了可视化的目的，给定一个双集群，数据矩阵的行和列可以重新排列，以使双集群连续。

算法在定义双集群的方式上有所不同。一些常见类型包括：

常量值、常量行或常量列
异常高或低值
低方差子矩阵
相关行或列

算法在如何将行和列分配给双集群方面也有所不同，这导致了不同的双集群结构。当行和列被分成分区时，就会出现块对角线或棋盘结构。

如果每一行和每一列都恰好属于一个双聚类，那么重新排列数据矩阵的行和列就会显示对角线上的双聚类。下面是这种结构的一个例子，其中双聚类具有比其他行和列更高的平均值：

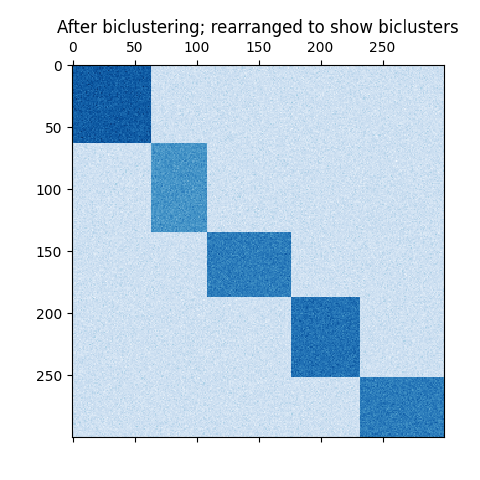
../_images/sphx_glr_plot_spectral_coclustering_003.png — 通过划分行和列形成的双集群的示例。#

在棋盘格情况下，每一行属于所有列集群，每一列属于所有行集群。以下是该结构的一个示例，其中每个双集群内的值的方差很小：

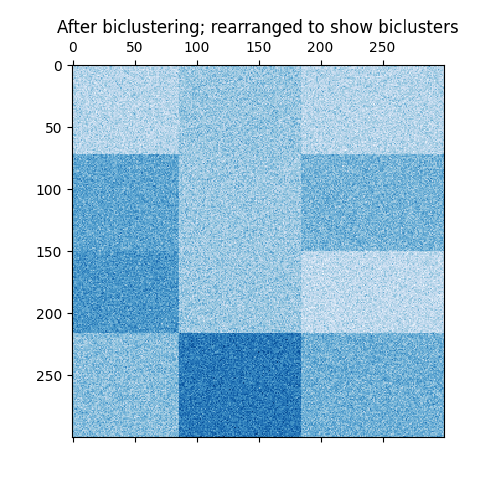
../_images/sphx_glr_plot_spectral_biclustering_003.png — 棋盘双簇的一个例子。#

匹配模型后，行和列集群成员资格可以在 rows_ 和 columns_ 美德.先知-愿 rows_[i] 是一个具有非零条目的二进制载体，对应于属于双集群的行 i .同样， columns_[i] 指示哪些列属于双集群 i .

一些模特还拥有 row_labels_ 和 column_labels_ 美德.先知-愿这些模型划分行和列，例如块对角线和棋盘双簇结构。

备注

Biclustering has many other names in different fields including co-clustering, two-mode clustering, two-way clustering, block clustering, coupled two-way clustering, etc. The names of some algorithms, such as the Spectral Co-Clustering algorithm, reflect these alternate names.

2.4.1. 光谱协同聚集#

的 SpectralCoclustering 算法查找值高于相应其他行和列中的值的双集群。每一行和每一列恰好属于一个双集群，因此重新排列行和列以使分区连续会显示对角线上的这些高值：

备注

该算法将输入数据矩阵视为二分图：矩阵的行和列对应于两组顶点，每个条目对应于行和列之间的边。该算法逼近该图的规范化切割以找到重子图。

2.4.1.1. 数学公式#

最佳正规化切割的大约解可以通过图的拉普拉斯的广义特征值分解来找到。通常这意味着直接使用拉普拉斯矩阵。如果原始数据矩阵 \(A\) 具有形状 \(m \times n\) ，相应二部图的拉普拉斯矩阵具有形状 \((m + n) \times (m + n)\) .然而，在这种情况下，可以直接与 \(A\) ，其更小且更高效。

输入矩阵 \(A\) 预处理如下：

\[A_n = R '{-1/2} A C '\]

哪里 \(R\) 是带入口的对角矩阵 \(i\) 等于 \(\sum_{j} A_{ij}\) 和 \(C\) 是带入口的对角矩阵 \(j\) 等于 \(\sum_{i} A_{ij}\) .

奇异值分解， \(A_n = U \Sigma V^\top\) ，提供的行和列的分区 \(A\) .左奇异向量的子集给出行分区，右奇异向量的子集给出列分区。

The \(\ell = \lceil \log_2 k \rceil\) singular vectors, starting from the second, provide the desired partitioning information. They are used to form the matrix \(Z\):

\[\begin{split}Z = \begin{bmatrix} R^{-1/2} U \\\\ C^{-1/2} V \end{bmatrix}\end{split}\]

那里的柱子 \(U\) 是 \(u_2, \dots, u_{\ell + 1}\) ，同样， \(V\) .

然后是一排排的 \(Z\) 使用聚集 k-means .第一 n_rows 标签提供行分区，其余的 n_columns 标签提供列分区。

示例

光谱协同聚集算法的演示：一个简单的例子，展示了如何使用双聚类生成数据矩阵并将此方法应用于它。
使用谱协同集群算法对文档进行二集群：在二十个新闻组数据集中寻找双集群的示例。

引用

Dhillon，Inderjit S，2001年。 Co-clustering documents and words using bipartite spectral graph partitioning

2.4.2. 光谱双集群#

的 SpectralBiclustering 算法假设输入数据矩阵具有隐藏的棋盘结构。具有这种结构的矩阵的行和列可以被划分，以便行集群和列集群的Cartesian积中的任何双集群的条目大致恒定。例如，如果有两个行分区和三个列分区，那么每一行将属于三个双集群，而每一列将属于两个双集群。

该算法对矩阵的行和列进行分区，以便相应的块常数棋盘矩阵提供对原始矩阵的良好逼近。

2.4.2.1. 数学公式#

输入矩阵 \(A\) 首先被规范化，使棋盘图案更加明显。有三种可能的方法：

Independent row and column normalization ，就像在光谱协同聚集中一样。此方法使行和为一个常数，而列和为一个不同的常数。
Bistochastization ：重复行和列规范化，直到收敛。此方法使行和列之和为相同的常数。
Log normalization: the log of the data matrix is computed: \(L = \log A\). Then the column mean \(\overline{L_{i \cdot}}\), row mean \(\overline{L_{\cdot j}}\), and overall mean \(\overline{L_{\cdot \cdot}}\) of \(L\) are computed. The final matrix is computed according to the formula

\[K_{ij} = L_{ij} - \overline{L_{i \cdot}} - \overline{L_{\cdot j}} + \overline{L_{\cdot \cdot}}\]

规范化后，计算前几个奇异载体，就像谱协同集群算法一样。

如果使用log正规化，则所有奇异载体都有意义。然而，如果使用独立正规化或双随机化，则第一奇异载体， \(u_1\) 和 \(v_1\) .都被丢弃了从现在开始，“第一个”奇异载体是指 \(u_2 \dots u_{p+1}\) 和 \(v_2 \dots v_{p+1}\) 除了对数归一化的情况之外。

给定这些奇异载体，根据哪一个可以最好地用分段常数载体逼近来对它们进行排名。使用一维k均值找到每个载体的近似值，并使用欧几里得距离进行评分。选择最佳左和右奇异载体的某个子集。接下来，将数据投影到奇异载体的最佳子集并进行集群。

例如，如果 \(p\) 计算奇异值， \(q\) 如所描述的那样找到最好的，其中 \(q<p\) .让 \(U\) 是一个矩阵， \(q\) 最佳左奇异载体，类似地 \(V\) 对于右边。要分区行， \(A\) 预计为 \(q\) 维度空间： \(A * V\) .处理 \(m\) 一排排的这个 \(m \times q\) 将矩阵作为样本并使用k均值进行聚集产生行标签。同样，将柱投影到 \(A^{\top} * U\) 并将其聚集起来 \(n \times q\) 矩阵生成列标签。

示例

光谱双集群算法的演示：一个简单的示例，展示了如何生成棋盘矩阵并对其进行双集群。

引用

Kluger，Yuval，et.阿尔。，2003. Spectral biclustering of microarray data: coclustering genes and conditions

2.4.3. 双集群评估#

评估双集群结果有两种方法：内部和外部。内部指标（例如集群稳定性）仅依赖于数据和结果本身。目前scikit-learn中没有内部双集群措施。外部措施是指外部信息来源，例如真正的解决方案。当处理真实数据时，真正的解决方案通常是未知的，但双集群人工数据可能对于精确评估算法很有用，因为真正的解决方案是已知的。

为了将一组找到的双聚类与一组真正的双聚类进行比较，需要两个相似性度量：一个是单个双聚类的相似性度量，另一个是将这些单个相似性组合成一个整体分数的方法。

为了比较单个双集群，使用了多种措施。目前，仅实现Jaccard指数：

\[J(A, B) = \frac{|A \cap B|}{|A| + |B| - |A \cap B|}\]

哪里 \(A\) 和 \(B\) 是双集群， \(|A \cap B|\) 是它们交集中的元素数。当双聚类完全不重叠时，Jaccard索引达到最小值0，当它们相同时，Jaccard索引达到最大值1。

已经开发了多种方法来比较两组双集群。目前，只有 consensus_score （Hochreiter et.阿尔。，2010年）可用：

使用Jaccard指数或类似的测量方法计算成对双集群（每套一个）的双集群相似性。
以一对一的方式将双集群从一组分配到另一组，以最大化其相似性的总和。此步骤是使用 scipy.optimize.linear_sum_assignment ，它使用修改后的Jonker-Volgenant算法。
相似性的最终总和除以较大集合的大小。

当所有双集群对完全不相同时，出现最低共识评分0。当两组相同时，最大得分为1。

引用

Hochreiter，Bodenhofer，et.阿尔。，2010. FABIA: factor analysis for bicluster acquisition .