2.6. 协方差估计#
许多统计问题需要估计总体的协方差矩阵,这可以被视为对数据集散点图形状的估计。大多数时候,此类估计必须对其性质(大小、结构、同质性)对估计质量有很大影响的样本进行。的 sklearn.covariance 该包提供了在各种设置下准确估计人口协方差矩阵的工具。
我们假设观察是独立且同分布的(i.i.d.)。
2.6.1. 经验协方差#
已知数据集的协方差矩阵可以很好地逼近经典 maximum likelihood estimator (or“经验协方差”),前提是观察的数量与特征(描述观察的变量)的数量相比足够大。更准确地说,样本的最大似然估计量是相应总体协方差矩阵的渐进无偏估计量。
The empirical covariance matrix of a sample can be computed using the
empirical_covariance function of the package, or by fitting an
EmpiricalCovariance object to the data sample with the
EmpiricalCovariance.fit method. Be careful that results depend
on whether the data are centered, so one may want to use the
assume_centered parameter accurately. More precisely, if
assume_centered=False, then the test set is supposed to have the
same mean vector as the training set. If not, both should be centered
by the user, and assume_centered=True should be used.
示例
看到 收缩协方差估计:LedoitWolf vs OAS和最大似然 例如如何安装
EmpiricalCovariance对象到数据。
2.6.2. 收缩协方差#
2.6.2.1. 基本收缩率#
尽管最大似然估计量是协方差矩阵的渐进无偏估计量,但它并不是协方差矩阵特征值的良好估计量,因此从其求逆中获得的精度矩阵并不准确。有时,甚至会出现经验协方差矩阵由于数字原因无法求反的情况。为了避免此类逆问题,引入了经验协方差矩阵的变换: shrinkage .
在scikit-learn中,这种转换(具有用户定义的收缩系数)可以直接应用于预先计算的协方差 shrunk_covariance 法此外,协方差的缩小估计量可以与具有 ShrunkCovariance 对象及其 ShrunkCovariance.fit 法同样,结果取决于数据是否集中,因此可能需要使用 assume_centered 参数准确。
Mathematically, this shrinkage consists in reducing the ratio between the smallest and the largest eigenvalues of the empirical covariance matrix. It can be done by simply shifting every eigenvalue according to a given offset, which is equivalent of finding the l2-penalized Maximum Likelihood Estimator of the covariance matrix. In practice, shrinkage boils down to a simple convex transformation : \(\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id\).
选择收缩量, \(\alpha\) 相当于设置偏差/方差权衡,下文将对此进行讨论。
示例
看到 收缩协方差估计:LedoitWolf vs OAS和最大似然 例如如何适应
ShrunkCovariance对象到数据。
2.6.2.2. 勒多伊特-沃尔夫萎缩#
在他们2004年的论文中 [1], O.勒多伊特和M.沃尔夫提出计算最佳收缩系数的公式 \(\alpha\) 这将最大限度地减少估计协方差矩阵和真实协方差矩阵之间的均方误差。
协方差矩阵的Ledoit-Wolf估计量可以在样本上使用 ledoit_wolf 功能 sklearn.covariance 包装,或者可以通过安装 LedoitWolf 反对同一样本。
备注
Case when population covariance matrix is isotropic
值得注意的是,当样本数量远远大于特征数量时,人们预计不需要收缩。这背后的直觉是,如果总体协方差是满等级的,当样本数量增加时,样本协方差也将变得正值。因此,不需要收缩,并且该方法应该自动做到这一点。
然而,当人口协方差恰好是单位矩阵的倍数时,Ledoit-Wolf程序中的情况并非如此。在这种情况下,随着样本数量的增加,Ledoit-Wolf收缩估计接近1。这表明Ledoit-Wolf意义上的协方差矩阵的最佳估计是单位的倍数。由于人口协方差已经是单位矩阵的倍数,因此Ledoit-Wolf解确实是一个合理的估计。
示例
看到 收缩协方差估计:LedoitWolf vs OAS和最大似然 例如如何适应
LedoitWolf以数据为对象,并根据可能性可视化Ledoit-Wolf估计器的性能。
引用
2.6.2.3. Oracle逼近收缩#
在假设数据呈高斯分布的情况下,Chen等人 [2] 推导出了一个公式,旨在选择一个收缩系数,该系数产生的均方误差小于Ledoit和Wolf公式给出的均方误差。由此产生的估计量称为协方差的Oracle收缩逼近估计量。
协方差矩阵的OAS估计量可以在样本上使用 oas 功能 sklearn.covariance 包装,或者可以通过安装 OAS 反对同一样本。
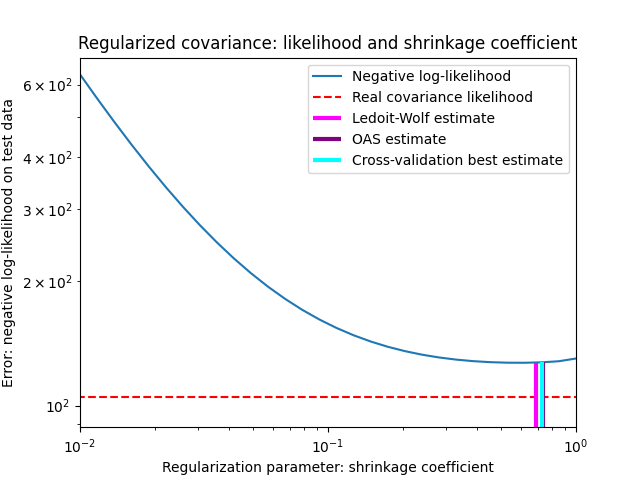
设置收缩时的偏差-方差权衡:比较Ledoit-Wolf和OAS估计量的选择#
引用
示例
看到 收缩协方差估计:LedoitWolf vs OAS和最大似然 例如如何安装
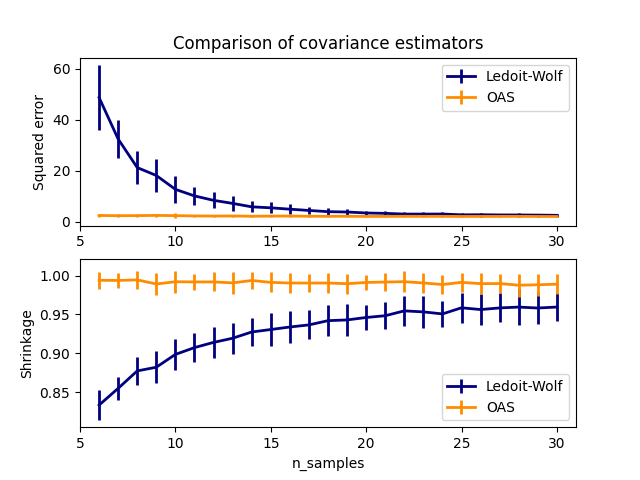
OAS对象到数据。看到 Ledoit-Wolf与OAS估计 为了可视化均方误差之间的差异,
LedoitWolf和OAS协方差的估计量。
2.6.3. 稀疏反协方差#
协方差矩阵的矩阵逆(通常称为精度矩阵)与偏相关矩阵成正比。它给出了部分独立关系。换句话说,如果两个特征在条件上独立于另一个特征,则精度矩阵中相应的系数将为零。这就是为什么估计稀疏精度矩阵是有意义的:协方差矩阵的估计通过从数据中学习独立关系来更好地调节。这被称为 covariance selection .
在小样本情况下,其中 n_samples 大约为 n_features 或更小的稀疏逆协方差估计量往往比收缩协方差估计量工作得更好。然而,在相反的情况下,或者对于非常相关的数据,它们可能在数值上不稳定。此外,与收缩估计器不同,稀疏估计器能够恢复非对角结构。
的 GraphicalLasso 估计器使用l1罚分来强制精度矩阵的稀疏性:它的精度越高 alpha 参数,精度矩阵越稀疏。相应的 GraphicalLassoCV 对象使用交叉验证来自动设置 alpha 参数.
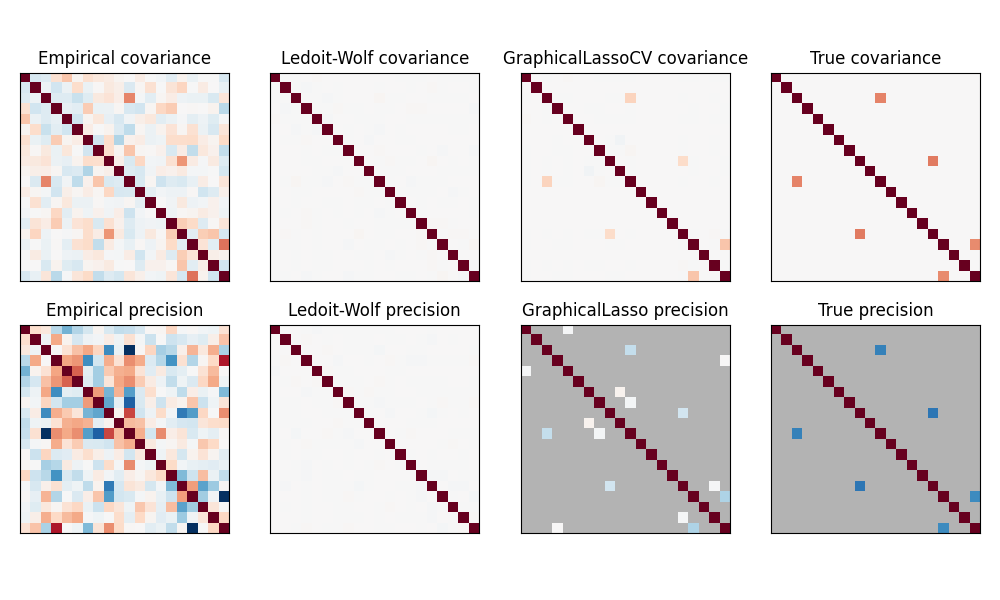
A comparison of maximum likelihood, shrinkage and sparse estimates of the covariance and precision matrix in the very small samples settings.#
备注
Structure recovery
从数据中的相关性恢复图形结构是一件具有挑战性的事情。如果你对这种恢复感兴趣,请记住:
从相关矩阵中恢复比从协方差矩阵中更容易:在运行之前标准化您的观察结果
GraphicalLasso如果基础图的节点的连接比平均节点多得多,则算法将错过其中一些连接。
如果您的观察数量与基础图形中的边数量相比并不大,则您将不会恢复它。
即使您处于有利的恢复条件下,也会通过交叉验证(例如使用
GraphicalLassoCV对象)将导致选择太多边。然而,相关边的权重将比不相关边重。
数学公式如下:
哪里 \(K\) 是要估计的精度矩阵,并且 \(S\) 是样本协方差矩阵。 \(\|K\|_1\) 是的非对角线系数绝对值的和 \(K\) .用于解决这个问题的算法是来自弗里德曼2008年生物统计学论文的格拉索算法。与R中的算法相同 glasso 包.
示例
引用
弗里德曼等人, "Sparse inverse covariance estimation with the graphical lasso" ,生物统计学9,第432页,2008年
2.6.4. 稳健协方差估计#
真实数据集通常会出现测量或记录错误。由于各种原因,也可能出现定期但不常见的观察结果。非常罕见的观察被称为异常值。上面介绍的经验协方差估计量和缩小协方差估计量对数据中异常值的存在非常敏感。因此,应该使用稳健的协方差估计器来估计其真实数据集的协方差。或者,鲁棒协方差估计器可以用于执行异常值检测并根据数据的进一步处理丢弃/淡化一些观察结果。
的 sklearn.covariance 包实现了协方差的稳健估计器,即最小协方差决定因子 [3].
2.6.4.1. 最小协方差行列式#
最小协方差决定性估计器是由PJ Ottseeuw在 [3]. 其想法是找到不是离群值的“良好”观察的给定比例(h),并计算其经验协方差矩阵。 然后重新调整该经验协方差矩阵以补偿所执行的观察选择(“一致性步骤”)。 计算出最小协方差决定性估计量后,可以根据观测的马哈拉诺比斯距离为观测值赋予权重,从而对数据集的协方差矩阵进行重新加权估计(“重新加权步骤”)。
尤利西斯和范德里森 [4] 开发了FastMCR算法以计算最小协方差决定元。将BCD对象与数据匹配时,在scikit-learn中使用该算法。FastBCD算法还同时计算数据集位置的稳健估计。
原始估计可通过以下方式访问: raw_location_ 和 raw_covariance_ 的属性 MinCovDet 稳健协方差估计器对象。
引用
PJ. seeuw。最小平方回归中位数。J. Am Stat Ass,79:871,1984。
一种最小协方差行列式估计的快速算法,1999,美国统计协会和美国质量协会,计量学。
示例
看到 稳健与经验协方差估计 例如如何适应
MinCovDet反对数据,看看在存在异常值的情况下估计如何保持准确。看到 稳健协方差估计和Mahalanobis距离相关性 来想象
EmpiricalCovariance和MinCovDet根据Mahalanobis距离进行协方差估计(因此我们也可以获得对精度矩阵的更好估计)。
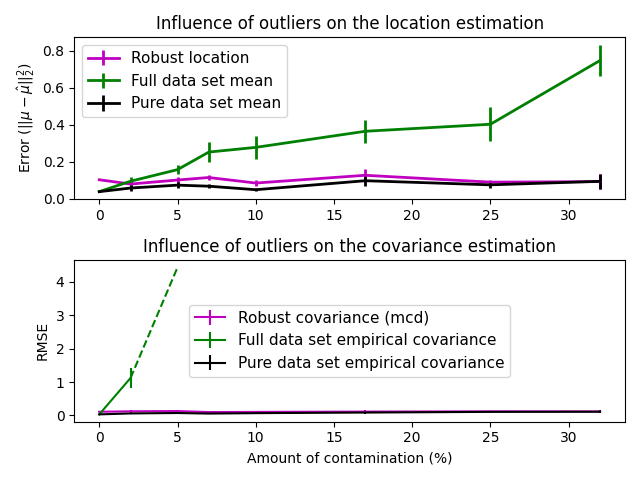
异常值对位置和协方差估计的影响 |
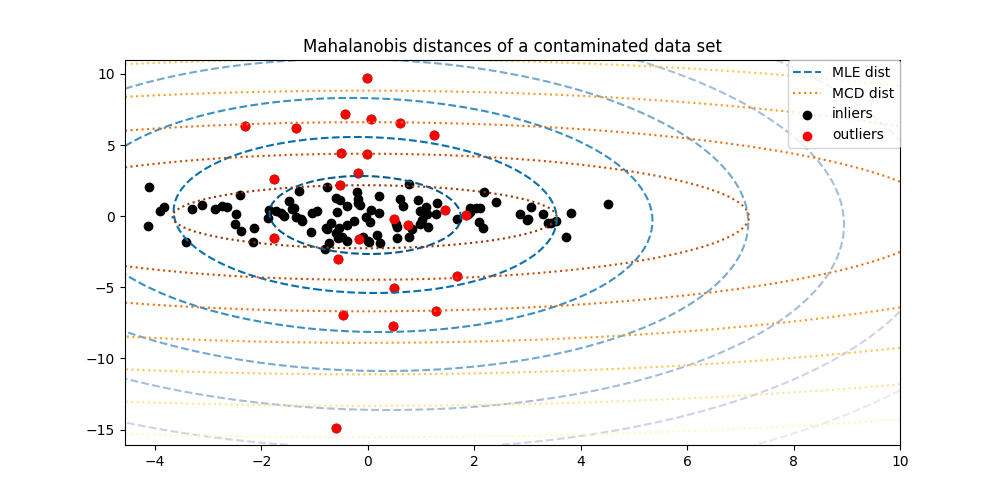
使用Mahalanobis距离分离内值和异常值 |
|---|---|