Sersic1D系列#

class astropy.modeling.functional_models.Sersic1D(amplitude=1, r_eff=1, n=4, **kwargs)[源代码]#

基类：Fittable1DModel

一维Sersic表面亮度分布。

参数:
amplitude : floatPython ：浮点

表面亮度为 r_eff 。

r_eff : floatPython ：浮点

有效(半光)半径。

n : floatPython ：浮点

控制轮廓形状的序列索引。的特定值 n 相当于以下配置文件：

  • N=4 : de Vaucouleurs \(r^{1/4}\) 轮廓

  • N=1：指数分布

  • N=0.5：高斯分布

其他参数:
fixed : dict ，可选Python：Dict，可选

字典 {{parameter_name: boolean}} 在拟合过程中不能改变的参数。True表示参数保持不变。或者 fixed 可以使用参数的属性。

tied : dict ，可选Python：Dict，可选

字典 {{parameter_name: callable}} 链接到其他参数的参数。字典值是提供链接关系的可调用项。或者 tied 可以使用参数的属性。

bounds : dict ，可选Python：Dict，可选

字典 {{parameter_name: value}} 参数的上下界。键是参数名。值是一个长度为2的列表或元组，为参数提供所需的范围。或者 min 和 max 可以使用参数的属性。

eqcons : list ，可选Python：列表，可选

长度函数列表 n 这样的话 eqcons[j](x0,*args) == 0.0 在一个成功优化的问题中。

ineqcons : list ，可选Python：列表，可选

长度函数列表 n 这样的话 ieqcons[j](x0,*args) >= 0.0 是一个成功优化的问题。

参见

Gaussian1D, Moffat1D, Lorentz1D

笔记

的 r 和 r_eff 输入必须具有兼容的单位或无单位数字。

模型公式：

\[I(r) = I_{e} \exp\left\{ -b_{n} \left[\left(\frac{r}{r_{e}}\right)^{(1/n)} -1\right]\right\}\]

哪里 \(I_{e}\) 是 amplitude 和 \(r_{e}\) 是 reff 。

常量 \(b_{n}\) 被定义为 \(r_{e}\) 包含总光度的一半。它可以从以下方程中进行数值求解：

\[\Gamma(2n)=2\Gamma(2n，b_{n})\]

哪里 \(\Gamma(a)\) 是 gamma function 和 \(\gamma(a, x)\) 是 lower incomplete gamma function 。

工具书类

实例

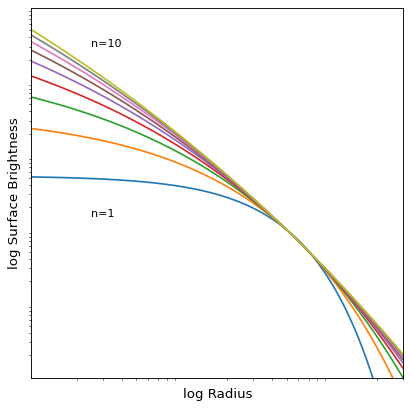
import numpy as np
from astropy.modeling.models import Sersic1D
import matplotlib.pyplot as plt

plt.figure()
plt.subplot(111, xscale='log', yscale='log')
s1 = Sersic1D(amplitude=1, r_eff=5)
r = np.arange(0, 100, 0.01)

for n in range(1, 10):
     s1.n = n
     plt.plot(r, s1(r))

plt.axis([1e-1, 30, 1e-2, 1e3])
plt.xlabel('log Radius')
plt.ylabel('log Surface Brightness')
plt.text(0.25, 1.5, 'n=1')
plt.text(0.25, 300, 'n=10')
plt.xticks([])
plt.yticks([])
plt.show()

(png, svg, pdf)

../_images/astropy-modeling-functional_models-Sersic1D-1.png

属性摘要

amplitude 

input_units 

此属性用于指示evaluate方法所需的单元或单元集，并返回将输入映射到单元（或 None 如果接受任何单位）。

n 

param_names 

描述此类型模型的参数的名称。

r_eff 

方法总结

evaluate(r, amplitude, r_eff, n)

一维Sersic剖面函数。

属性文档

amplitude = Parameter('amplitude', value=1.0)#
input_units#
n = Parameter('n', value=4.0)#
param_names = ('amplitude', 'r_eff', 'n')#

描述此类型模型的参数的名称。

此元组中的参数与初始化特定类型的模型时应传入的顺序相同。某些类型的模型，如多项式模型，根据模型的某些其他属性（如阶数）有不同数量的参数。

定义自定义模型类时，此属性的值由 Parameter 在类中定义的body属性。

r_eff = Parameter('r_eff', value=1.0)#

方法文件

classmethod evaluate(r, amplitude, r_eff, n)[源代码]#

一维Sersic剖面函数。