Ctrl+K

物理模型#

这些模型都是物理驱动的，通常作为物理问题的解决方案。这与那些通常作为数学问题解决方案的数学动机形成鲜明对比。

BlackBody#

这个 BlackBody 模型提供了一个用于 Planck's Law . 黑体函数是

\[B{\nu}（T）=A\frac{2h\nu^{3}/c^{2}}{exp（h\nu/kt）-1}\]

在哪里？ \(\nu\) 是频率， \(T\) 是温度， \(A\) 是比例因子， \(h\) 普朗克常数， \(c\) 是光速 \(k\) 玻尔兹曼常数。

模型的两个参数：比例因子 scale （A） 以及绝对温度 temperature （T） 一。如果 scale 因子没有单位，则结果是以光谱辐射度为单位，特别是ergs/（cm^2 Hz s sr）。如果 scale 因子与光谱辐射度单位一起传递，则结果以这些单位表示（例如，ergs/（cm^2 A s sr）或MJy/sr）。设置 scale 单位为ergs/（cm^2 A s sr）的因子将使普朗克函数为 \(B_\lambda\) . 温度可以通过任何支持的温度单位作为一个量传递。

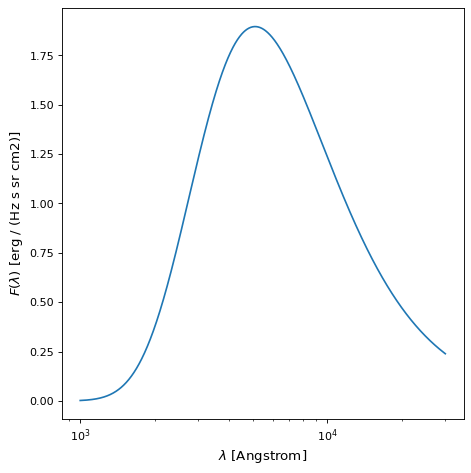
下面是一个温度为10000 K，标度为1的黑体的示例图。小数位数为1表示普朗克函数，返回的默认单位没有缩放 BlackBody .

import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import BlackBody
import astropy.units as u

wavelengths = np.logspace(np.log10(1000), np.log10(3e4), num=1000) * u.AA

# blackbody parameters
temperature = 10000 * u.K

# BlackBody provides the results in ergs/(cm^2 Hz s sr) when scale has no units
bb = BlackBody(temperature=temperature, scale=10000.0)
bb_result = bb(wavelengths)

fig, ax = plt.subplots(ncols=1)
ax.plot(wavelengths, bb_result, '-')

ax.set_xscale('log')
ax.set_xlabel(fr"$\lambda$ [{wavelengths.unit}]")
ax.set_ylabel(fr"$F(\lambda)$ [{bb_result.unit}]")

plt.tight_layout()
plt.show()

(png, svg, pdf)

../_images/physical_models-1.png

这个 bolometric_flux() 成员函数使用 \(\sigma T^4/\pi\) 在哪里？ \(\sigma\) 是Stefan Boltzmann常数。

这个 lambda_max() 和 nu_max() 成员函数给出了 \(B_\lambda\) 和 \(B_\nu\) ，分别使用 Wien's Law .

德鲁德1D#

这个 Drude1D 模型提供了一个材料中电子行为的模型（参见 Drude Model ). 就像 Lorentz1D 模型，德鲁德模型的翅膀比 Gaussian1D 模型。德鲁德剖面已用于模拟尘埃特征，包括2175埃消光特征和中红外芳香族/PAH特征。德鲁德在 \(x\) 是

\[D（x）=A\frac{（f/x_0）^2}{（（x/x_0-x 0/x）^2+（f/x_0）^2}\]

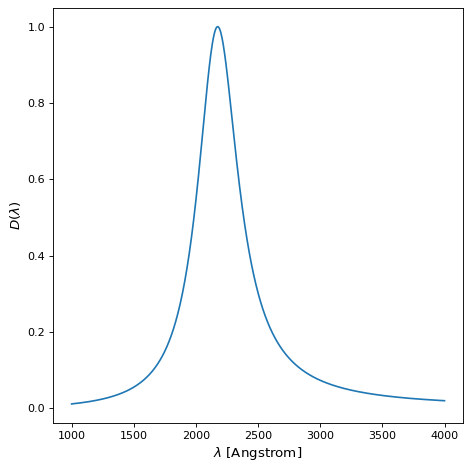
在哪里？ \(A\) 是振幅， \(f\) 是最大宽度的一半，以及 \(x_0\) 是中心波长。Drude1D模型的示例 \(x_0 = 2175\) 埃和 \(f = 400\) 埃如下所示。

import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import Drude1D
import astropy.units as u

wavelengths = np.linspace(1000, 4000, num=1000) * u.AA

# Parameters and model
mod = Drude1D(amplitude=1.0, x_0=2175. * u.AA, fwhm=400. * u.AA)
mod_result = mod(wavelengths)

fig, ax = plt.subplots(ncols=1)
ax.plot(wavelengths, mod_result, '-')

ax.set_xlabel(fr"$\lambda$ [{wavelengths.unit}]")
ax.set_ylabel(r"$D(\lambda)$")

plt.tight_layout()
plt.show()

(png, svg, pdf)

../_images/physical_models-2.png

NFW#

这个 NFW 该模型计算了一维纳瓦罗-弗伦克-怀特轮廓。NFW剖面中的暗物质密度由以下公式给出：

\[\rho（r）=\frac{\delta_c\rho{c}{r/r\u s（1+r/r\u s）^2}\]

在哪里？ \(\rho_{{c}}\) 是轮廓红移时宇宙的临界密度， \(\delta_c\) 是过密度，以及 \(r_s\) 是轮廓的缩放半径。

该模型依赖于三个参数：

mass ：剖面的质量（如果未提供单位，则以太阳质量为单位）

concentration ：剖面浓度

redshift ：外形的红移

以及两个可选的初始化变量：

massfactor ：指定过敏感类型和因子的元组或字符串（默认值为“临界”，200））

cosmo ：用于密度计算的宇宙学（默认默认值_宇宙学）

备注

评估前需要初始化NFW轮廓物体（以便设置质量过密度和宇宙学）。

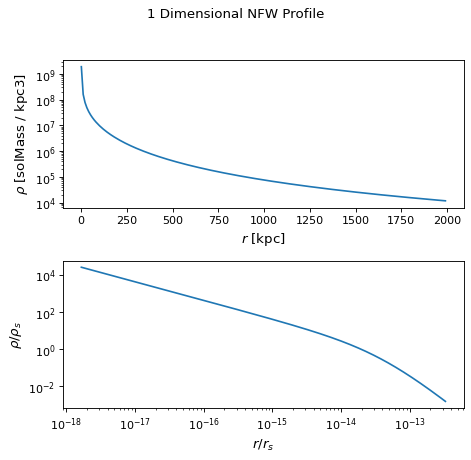
具有以下参数的NFW剖面图示例如下所示：

mass = \(2.0 x 10^{15} M_{sun}\)

concentration =8.5

redshift =0.63

第一张图是NFW剖面密度与半径的函数关系。第二个绘图分别显示由NFW比例密度和比例半径规范化的剖面密度和半径。“缩放密度”（scale density）和“缩放半径”（scale radius）可用作属性 rho_s 和 r_s ，可通过 r_virial .

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import NFW
import astropy.units as u
from astropy import cosmology

# NFW Parameters
mass = u.Quantity(2.0E15, u.M_sun)
concentration = 8.5
redshift = 0.63
cosmo = cosmology.Planck15
massfactor = ("critical", 200)

# Create NFW Object
n = NFW(mass=mass, concentration=concentration, redshift=redshift, cosmo=cosmo,
        massfactor=massfactor)

# Radial distribution for plotting
radii = range(1,2001,10) * u.kpc

# Radial NFW density distribution
n_result = n(radii)

# Plot creation
fig, ax = plt.subplots(2)
fig.suptitle('1 Dimensional NFW Profile')

# Density profile subplot
ax[0].plot(radii, n_result, '-')
ax[0].set_yscale('log')
ax[0].set_xlabel(fr"$r$ [{radii.unit}]")
ax[0].set_ylabel(fr"$\rho$ [{n_result.unit}]")

# Create scaled density / scaled radius subplot
# NFW Object
n = NFW(mass=mass, concentration=concentration, redshift=redshift, cosmo=cosmo,
        massfactor=massfactor)

# Radial distribution for plotting
radii = np.logspace(np.log10(1e-5), np.log10(2), num=1000) * u.Mpc
n_result = n(radii)

# Scaled density / scaled radius subplot
ax[1].plot(radii / n.radius_s, n_result / n.density_s, '-')
ax[1].set_xscale('log')
ax[1].set_yscale('log')
ax[1].set_xlabel(r"$r / r_s$")
ax[1].set_ylabel(r"$\rho / \rho_s$")

# Display plot
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

(png, svg, pdf)

../_images/physical_models-3.png

这个 circular_velocity() 构件提供每个位置的圆速度 r 通过方程式：

\[v{circ}（r）^2=\frac{1}{x}\frac{\ln（1+cx）-（cx）/（1+cx）}{\ln（1+c）-c/（1+c）}\]

其中x是比率 r ：数学：/r_{vir}。圆速度是以公里/秒为单位提供的。

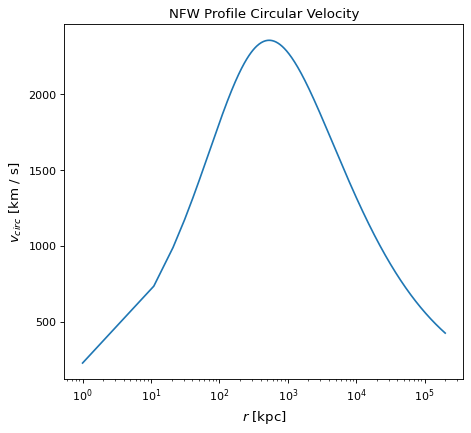
具有以下参数的NFW剖面的圆速度示例图如下所示：

mass = \(2.0 x 10^{15} M_{sun}\)

concentration =8.5

redshift =0.63

“最大圆速度”和“最大圆速度半径”作为属性可用 v_max 和 r_max .

import matplotlib.pyplot as plt
from astropy.modeling.models import NFW
import astropy.units as u
from astropy import cosmology

# NFW Parameters
mass = u.Quantity(2.0E15, u.M_sun)
concentration = 8.5
redshift = 0.63
cosmo = cosmology.Planck15
massfactor = ("critical", 200)

# Create NFW Object
n = NFW(mass=mass, concentration=concentration, redshift=redshift, cosmo=cosmo,
        massfactor=massfactor)

# Radial distribution for plotting
radii = range(1,200001,10) * u.kpc

# NFW circular velocity distribution
n_result = n.circular_velocity(radii)

# Plot creation
fig,ax = plt.subplots()
ax.set_title('NFW Profile Circular Velocity')
ax.plot(radii, n_result, '-')
ax.set_xscale('log')
ax.set_xlabel(fr"$r$ [{radii.unit}]")
ax.set_ylabel(r"$v_{circ}$" + f" [{n_result.unit}]")

# Display plot
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

(png, svg, pdf)

../_images/physical_models-4.png

宇宙学#

的实例 Cosmology 类(和子类)包括|Cosmology.to_Format|，这是一种将Cosmology转换为另一个Python对象的方法。具体地说，任何红移方法都可以转换为 FittableModel 使用参数实例化 format="astropy.model" 。在转换过程中，每个 Cosmology Parameter 被转换为 astropy.modeling.Model Parameter ，而红移方法则成为模型的 __call__ / evaluate 方法。这意味着宇宙学现在可以用数据来拟合了！

>>> from astropy.cosmology import Planck18
>>> model = Planck18.to_format(format="astropy.model", method="lookback_time")
>>> model
<FlatLambdaCDMCosmologyLookbackTimeModel(H0=67.66 km / (Mpc s), Om0=0.30966,
    Tcmb0=2.7255 K, Neff=3.046, m_nu=[0.  , 0.  , 0.06] eV, Ob0=0.04897,
    name='Planck18')>

完成后，例如试衣，可以将模型转换回 Cosmology 使用|Cosmology.from_Format|。

>>> from astropy.cosmology import Cosmology
>>> cosmo = Cosmology.from_format(model, format="astropy.model")
>>> cosmo == Planck18
True
On this page
Edit on GitHub