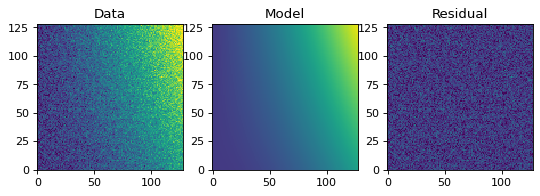模型与数据拟合#
这个模块为一些Numpy和Scipy fitting函数提供了包装器,称为Fitters。所有装配工都可以称为函数。他们举了一个例子 FittableModel 作为输入并修改其 parameters 属性。这样做的目的是使其具有可扩展性,并允许用户方便地添加其他装配工。
用Numpy‘s进行线性拟合 numpy.linalg.lstsq 功能。目前有一些非线性装配工使用 scipy.optimize.leastsq , scipy.optimize.least_squares ,以及 scipy.optimize.fmin_slsqp 。
将输入传递给装配工的规则如下:
非线性装配工当前仅处理单个模型(而不是模型集)。
线性装配工可以将单个输入拟合到多个模型集,从而创建多个拟合模型。这可能需要指定
model_set_axis参数,就像评估模型时使用的一样;这可能是装配工知道如何广播输入数据所必需的。这个
LinearLSQFitter目前只适用于简单(不是复合)模型。当前的拟合器只处理具有单一输出的模型(包括双变量函数,如
Chebyshev2D但不是映射的复合模型x, y -> x', y')拟合数据和模型参数的单位在拟合之前被剥离,以便基础
scipy方法可以处理这些数据。当将数据与单位进行拟合时,应注意这一点,因为单位转换只会在最初执行。这些转换将使用equivalencies向钳工提供的参数与model.input_units_equivalencies适合的模型的属性。
备注
通常,非线性拟合不支持对包含非限定值的数据进行拟合: NaN , Inf ,或 -Inf 。这是底层Scipy库的限制。因此,只要待拟合的数据中存在任何非有限值,就会产生误差。为了避免这个错误,用户应该从他们的数据中“过滤”非限定值,例如,在拟合 model ,带有一个 fitter 使用 data 对于包含非有限值的情况,我们可以按如下方式对这些问题进行“过滤”:
# Filter non-finite values from data
mask = np.isfinite(data)
# Fit model to filtered data
model = fitter(model, x[mask], data[mask])
或对于2D情况::
# Filter non-finite values from data
mask = np.isfinite(data)
# Fit model to filtered data
model = fitter(model, x[mask], y[mask], data[mask])
关于非线性拟合的几点注记#
有几种非线性适配器,它们依赖于几种不同的优化算法。您应该选择哪一个将取决于您试图解决的问题。主要推荐的非线性适合者是:
TRFLSQFitter,它使用信任区域反射(TRF)算法,该算法特别适合有边界的大型稀疏问题,请参阅scipy.optimize.least_squares了解更多详细信息。DogBoxLSQFitter,它使用具有矩形信任区域的狗腿算法,典型的用例是有边界的小问题。不建议针对等级不足的Jacobian问题,请参阅scipy.optimize.least_squares了解更多详细信息。LMLSQFitter,它使用Levenberg-Marquardt(LM)算法,由scipy.optimize.least_squares.不处理边界和/或稀疏Jacobian。通常是解决小型无约束问题的最有效方法。如果您的问题需要Levenberg-Marquardt算法,现在建议您使用该Fitter而不是LevMarLSQFitter因为它使用了scipy中该算法的推荐版本。然而,如果您的问题使用边界,则应该使用另一个非线性Fitter,例如TRFLSQFitter或DogBoxLSQFitter
注意到 LevMarLSQFitter fitter,通过scipy遗留功能使用Levenberg-Marquardt算法 scipy.optimize.leastsq ,不再推荐。该配合器通过简单的最小/最大条件支持参数界限,从而在配合的每个步骤期间,超出界限的参数只需重置为界限的最小或最大。如果在匹配过程中参数接近边界,这可能会导致参数“坚持”到其中一个边界。如果您正在调整的模型利用界限,则应使用其他调整器之一,例如 TRFLSQFitter 或 DogBoxLSQFitter ,如果您不需要边界并且特别想使用Levenberg-Marquardt算法,则应该使用 LMLSQFitter .
简单的一维模型拟合#
在本节中,我们将看到一个将高斯拟合到模拟数据集的简单示例。公司现采用国际 Gaussian1D 和 Trapezoid1D 模型和 TRFLSQFitter 适合数据的调整者:
import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models, fitting
# Generate fake data
rng = np.random.default_rng(0)
x = np.linspace(-5., 5., 200)
y = 3 * np.exp(-0.5 * (x - 1.3)**2 / 0.8**2)
y += rng.normal(0., 0.2, x.shape)
# Fit the data using a box model.
# Bounds are not really needed but included here to demonstrate usage.
t_init = models.Trapezoid1D(amplitude=1., x_0=0., width=1., slope=0.5,
bounds={"x_0": (-5., 5.)})
fit_t = fitting.TRFLSQFitter()
t = fit_t(t_init, x, y, maxiter=200)
# Fit the data using a Gaussian
g_init = models.Gaussian1D(amplitude=1., mean=0, stddev=1.)
fit_g = fitting.TRFLSQFitter()
g = fit_g(g_init, x, y)
# Plot the data with the best-fit model
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(x, y, 'ko')
ax.plot(x, t(x), label='Trapezoid')
ax.plot(x, g(x), label='Gaussian')
ax.set(xlabel='Position', ylabel='Flux')
ax.legend(loc=2)
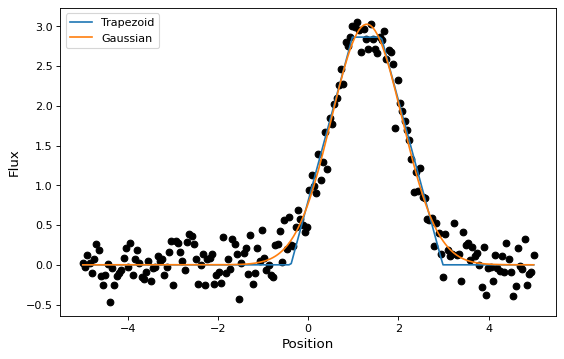
如上所示,一旦实例化,fitter类就可以作为接受初始模型的函数使用 (t_init 或 g_init )以及数据值 (x 和 y ),并返回已安装的模型 (t 或 g )
简单的二维模型拟合#
类似于一维的例子,我们可以创建一个模拟的二维数据集,并拟合一个多项式模型。例如,这可以用来调整图像的背景。
import warnings
import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models, fitting
from astropy.utils.exceptions import AstropyUserWarning
# Generate fake data
rng = np.random.default_rng(0)
y, x = np.mgrid[:128, :128]
z = 2. * x ** 2 - 0.5 * x ** 2 + 1.5 * x * y - 1.
z += rng.normal(0., 0.1, z.shape) * 50000.
# Fit the data using astropy.modeling
p_init = models.Polynomial2D(degree=2)
fit_p = fitting.LMLSQFitter()
with warnings.catch_warnings():
# Ignore model linearity warning from the fitter
warnings.filterwarnings('ignore', message='Model is linear in parameters',
category=AstropyUserWarning)
p = fit_p(p_init, x, y, z)
# Plot the data with the best-fit model
fig, axs = plt.subplots(figsize=(8, 2.5), ncols=3)
ax1 = axs[0]
ax1.imshow(z, origin='lower', interpolation='nearest', vmin=-1e4, vmax=5e4)
ax1.set_title("Data")
ax2 = axs[1]
ax2.imshow(p(x, y), origin='lower', interpolation='nearest', vmin=-1e4,
vmax=5e4)
ax2.set_title("Model")
ax3 = axs[2]
ax3.imshow(z - p(x, y), origin='lower', interpolation='nearest', vmin=-1e4,
vmax=5e4)
ax3.set_title("Residual")