模型#
基础#
这个 astropy.modeling 包将在单个命名空间下收集的多个模型定义为 astropy.modeling.models . 模型的行为类似于参数化函数:
>>> import numpy as np
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=1.2, mean=0.9, stddev=0.5)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Parameters:
amplitude mean stddev
--------- ---- ------
1.2 0.9 0.5
可作为模型属性访问:
>>> g.amplitude
Parameter('amplitude', value=1.2)
>>> g.mean
Parameter('mean', value=0.9)
>>> g.stddev
Parameter('stddev', value=0.5, bounds=(1.1754943508222875e-38, None))
也可以通过以下属性进行更新:
>>> g.amplitude = 0.8
>>> g.amplitude
Parameter('amplitude', value=0.8)
可以通过将模型称为函数来评估它们:
>>> g(0.1)
0.22242984036255528
>>> g(np.linspace(0.5, 1.5, 7))
array([0.58091923, 0.71746405, 0.7929204 , 0.78415894, 0.69394278,
0.54952605, 0.3894018 ])
正如上面的示例所示,一般情况下,大多数模型都根据标准来评估类似数组的输入 Numpy broadcasting rules 对于数组。因此,模型已经可以用来评估共同的功能,独立于软件包的拟合特性。
实例化和评估模型#
通常,通过向构造函数提供定义模型实例的参数值来实例化模型,如 参数 .
另外,一个 Model 实例可以用一组参数表示单个模型,或者 Model set 由一组参数组成,每个参数代表同一参数模型的不同参数化。例如,可以用一个平均值、标准差和振幅实例化一个高斯模型。或者你可以创建一组N高斯函数,其中每一个都将在图像立方体中的不同平面上进行计算。
例如,单个高斯模型可以用所有标量参数实例化:
>>> from astropy.modeling.models import Gaussian1D
>>> g = Gaussian1D(amplitude=1, mean=0, stddev=1)
>>> g
<Gaussian1D(amplitude=1., mean=0., stddev=1.)>
新创建的模型实例 g 现在就像高斯函数一样有特定的参数。只需要一个输入:
>>> g.inputs
('x',)
>>> g(x=0)
1.0
也可以在不显式使用关键字参数的情况下调用模型:
>>> g(0)
1.0
或者可以通过传递多个参数值来实例化一组高斯:
>>> from astropy.modeling.models import Gaussian1D
>>> gset = Gaussian1D(amplitude=[1, 1.5, 2],
... mean=[0, 1, 2],
... stddev=[1., 1., 1.],
... n_models=3)
>>> print(gset)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 3
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 1.0
1.5 1.0 1.0
2.0 2.0 1.0
这个模型的工作原理也类似于高斯函数。模型集中的三个模型可以在同一输入上求值:
>>> gset(1.)
array([0.60653066, 1.5 , 1.21306132])
或在 N=3 输入:
>>> gset([1, 2, 3])
array([0.60653066, 0.90979599, 1.21306132])
有关拟合模型集的综合示例,请参见 拟合模型集 .
模型反转#
所有型号都有 Model.inverse 属性,对于某些模型,它可能返回一个新模型,该模型是它所附加到的模型的解析逆。例如::
>>> from astropy.modeling.models import Linear1D
>>> linear = Linear1D(slope=0.8, intercept=1.0)
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
一个模型的逆对象总是一个完全实例化的模型,因此可以直接计算如下:
>>> linear.inverse(2.0)
1.25
也可以指定 习俗 与模型相反。例如,当一个模型没有解析逆,但可能有一个用数值计算并由另一个模型表示的近似逆的情况下,这可能是有用的。即使目标模型有一个默认的解析逆函数——在本例中,默认值被自定义逆函数覆盖:
>>> from astropy.modeling.models import Polynomial1D
>>> linear.inverse = Polynomial1D(degree=1, c0=-1.25, c1=1.25)
>>> linear.inverse
<Polynomial1D(1, c0=-1.25, c1=1.25)>
如果已将自定义反转指定给模型,则可以使用 del model.inverse . 这会将反转重置为其默认值(如果存在)。如果不存在默认值,则访问 model.inverse 提高 NotImplementedError . 例如,多项式模型没有默认的逆:
>>> del linear.inverse
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
>>> p = Polynomial1D(degree=2, c0=1.0, c1=2.0, c2=3.0)
>>> p.inverse
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "astropy\modeling\core.py", line 796, in inverse
raise NotImplementedError("An analytical inverse transform has not "
NotImplementedError: No analytical or user-supplied inverse transform
has been implemented for this model.
我们当然可以计算一个逆函数,然后把它赋给一个多项式模型。
备注
为模型指定自定义逆时,不执行任何验证以确保它实际上是一个逆或甚至近似逆。所以你自己承担风险来分配定制反转。
边界框#
基于边界盒的高效模型渲染#
所有 Model 子类具有 bounding_box 属性,该属性可用于设置模型的有效限制。当输入范围远大于模型本身的特征宽度时,大大提高了评价效率。例如,要从大型测量目录创建天空模型图像,每个源只应在其贡献大量通量的像素上进行评估。否则,对于一个普通的CPU来说,这个任务在计算上可能是禁止的。
这个 Model.render 方法可用于计算输出数组或输入坐标数组上的模型,将计算限制为 bounding_box 区域(如果已设置)。如果没有传递其他输入数组,此函数还将生成模型的邮票图像。要从数据数组本身提取邮票,请参阅 二维剪切图像 .
使用标准边界框#
有关基本用法,请参见 Model.bounding_box 。默认情况下为no bounding_box 是设置的,但在模型子类上设置 bounding_box 属性或方法是显式定义的。然后,缺省值是围绕完全包含模型的位置对称的最小矩形区域。如果模型没有有限的范围,文档中会注明遏制标准。例如,请参见 Gaussian2D.bounding_box 。
警告
访问 Model.bounding_box 属性在尚未设置或没有默认设置时将导致 NotImplementedError 。如果此行为不受欢迎,则可以改用 Model.get_bounding_box 方法,而不是。如果存在边界框(通过设置或默认),此方法将返回边界框,否则将返回 None 而不是引发错误。
A Model.bounding_box 用户可以将默认设置为任何可调用对象。这对于使用创建的模型特别有用 custom_model 或作为一种 CompoundModel **
>>> from astropy.modeling import custom_model
>>> def ellipsoid(x, y, z, x0=0, y0=0, z0=0, a=2, b=3, c=4, amp=1):
... rsq = ((x - x0) / a) ** 2 + ((y - y0) / b) ** 2 + ((z - z0) / c) ** 2
... val = (rsq < 1) * amp
... return val
...
>>> class Ellipsoid3D(custom_model(ellipsoid)):
... # A 3D ellipsoid model
... def bounding_box(self):
... return ((self.z0 - self.c, self.z0 + self.c),
... (self.y0 - self.b, self.y0 + self.b),
... (self.x0 - self.a, self.x0 + self.a))
...
>>> model1 = Ellipsoid3D()
>>> model1.bounding_box
ModelBoundingBox(
intervals={
x0: Interval(lower=-2.0, upper=2.0)
x1: Interval(lower=-3.0, upper=3.0)
x2: Interval(lower=-4.0, upper=4.0)
}
model=Ellipsoid3D(inputs=('x0', 'x1', 'x2'))
order='C'
)
默认情况下,模型将根据任何输入进行评估。通过传递标志,它们只能在边界框内的输入上求值。对于边界框a之外的输入 fill_value 返回 (np.nan 默认情况下):
>>> model1(-5, 1, 1)
0.0
>>> model1(-5, 1, 1, with_bounding_box=True)
nan
>>> model1(-5, 1, 1, with_bounding_box=True, fill_value=-1)
-1.0
Model.bounding_box 可以通过使用属性设置器在任何模型实例上进行设置。例如,对于单个输入模型,只需设置下界和上界的元组:
>>> from astropy.modeling.models import Polynomial1D
>>> model2 = Polynomial1D(2)
>>> model2.bounding_box = (-1, 1)
>>> model2.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
}
model=Polynomial1D(inputs=('x',))
order='C'
)
>>> model2(-2)
0.0
>>> model2(-2, with_bounding_box=True)
nan
>>> model2(-2, with_bounding_box=True, fill_value=47)
47.0
对于多输入模型, Model.bounding_box 可以通过指定下限/上限元组的元组在任何模型实例上进行设置:
>>> from astropy.modeling.models import Polynomial2D
>>> model3 = Polynomial2D(2)
>>> model3.bounding_box = ((-2, 2), (-1, 1))
>>> model3.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
y: Interval(lower=-2, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='C'
)
>>> model3(-2, 0)
0.0
>>> model3(-2, 0, with_bounding_box=True)
nan
>>> model3(-2, 0, with_bounding_box=True, fill_value=7)
7.0
请注意,如果要直接恢复用于形成边界框的元组,则可以使用 ModelBoundingBox.bounding_box() 方法:
>>> model1.bounding_box.bounding_box()
((np.float64(-4.0), np.float64(4.0)), (np.float64(-3.0), np.float64(3.0)), (np.float64(-2.0), np.float64(2.0)))
>>> model2.bounding_box.bounding_box()
(-1, 1)
>>> model3.bounding_box.bounding_box()
((-2, 2), (-1, 1))
警告
设置多维边界框时,请务必记住,默认情况下,假定元组的元组为 'C' 已排序,这意味着绑定的元组将以与其各自的输入顺序相反的顺序进行排序。也就是说,如果输入的顺序是 ('x', 'y', 'z') 则需要将界限列在 ('z', 'y', 'x') 秩序。
如果用户不想直接使用默认设置 'C' 已订购包围盒。可以使用替代方案 'F' 排序,它按照与输入相同的顺序对边框元组进行排序。要做到这一点,可以使用 bind_bounding_box 函数,并将 order='F' 关键字参数::
>>> from astropy.modeling import bind_bounding_box
>>> model4 = Polynomial2D(3)
>>> bind_bounding_box(model4, ((-1, 1), (-2, 2)), order='F')
>>> model4.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
y: Interval(lower=-2, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
>>> model4(-2, 0)
0.0
>>> model4(-2, 0, with_bounding_box=True)
nan
>>> model4(-2, 0, with_bounding_box=True, fill_value=12)
12.0
>>> model4.bounding_box.bounding_box()
((-1, 1), (-2, 2))
>>> model4.bounding_box.bounding_box(order='C')
((-2, 2), (-1, 1))
警告
当前,在组合模型时,只有在将模型与 & 操作员。对于其他运算符,必须显式指定复合模型的边界框。将来的版本将尽可能为复合模型确定适当的边界框。
使用复合边界框#
有时,同一模型有多个边界框很有用,在评估模型时可以选择这些边框。在这种情况下,应考虑使用 CompoundBoundingBox 。
这种情况的一个常见用例可能是,如果模型具有单个“离散”选择器输入(例如 'slit_id' ),其中确定应该将什么边界框应用于其他输入。为此,首先需要定义边界框元组的字典,字典键是与该特定边界框对应的选择器输入的特定值::
>>> from astropy.modeling.models import Shift, Identity
>>> model1 = Shift(1) & Shift(2) & Identity(1)
>>> model1.inputs = ('x', 'y', 'slit_id')
>>> bboxes = {
... 0: ((0, 1), (1, 2)),
... 1: ((2, 3), (3, 4))
... }
为了使复合边界框起作用,必须指定一个选择器参数列表,其中该列表的元素是输入名称的元组,以及边界框是否应该应用于选择器参数。在本例中,忽略选择器参数是有意义的:
>>> from astropy.modeling.core import bind_compound_bounding_box
>>> selector_args = [('slit_id', True)]
>>> bind_compound_bounding_box(model1, bboxes, selector_args, order='F')
>>> model1.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
ignored=['slit_id']
model=CompoundModel(inputs=('x', 'y', 'slit_id'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
ignored=['slit_id']
model=CompoundModel(inputs=('x', 'y', 'slit_id'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='slit_id', ignore=True)
)
)
>>> model1(0.5, 1.5, 0, with_bounding_box=True)
(1.5, 3.5, 0.0)
>>> model1(0.5, 1.5, 1, with_bounding_box=True)
(np.float64(nan), np.float64(nan), np.float64(nan))
还可以使用多个选择器参数,在这种情况下,需要将边界框词典的键指定为值的元组:
>>> model2 = Shift(1) & Shift(2) & Identity(2)
>>> model2.inputs = ('x', 'y', 'slit_x', 'slit_y')
>>> bboxes = {
... (0, 0): ((0, 1), (1, 2)),
... (0, 1): ((2, 3), (3, 4)),
... (1, 0): ((4, 5), (5, 6)),
... (1, 1): ((6, 7), (7, 8)),
... }
>>> selector_args = [('slit_x', True), ('slit_y', True)]
>>> bind_compound_bounding_box(model2, bboxes, selector_args, order='F')
>>> model2.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0, 0) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(0, 1) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(1, 0) = ModelBoundingBox(
intervals={
x: Interval(lower=4, upper=5)
y: Interval(lower=5, upper=6)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(1, 1) = ModelBoundingBox(
intervals={
x: Interval(lower=6, upper=7)
y: Interval(lower=7, upper=8)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='slit_x', ignore=True)
Argument(name='slit_y', ignore=True)
)
)
>>> model2(0.5, 1.5, 0, 0, with_bounding_box=True)
(1.5, 3.5, 0.0, 0.0)
>>> model2(0.5, 1.5, 1, 1, with_bounding_box=True)
(np.float64(nan), np.float64(nan), np.float64(nan), np.float64(nan))
属性指定组成复合边界的所有边界框的顺序。 order 关键字参数。
这种情况的另一个用例可能是,如果想要对同一模型使用多个边界框,其中用户在评估模型时选择边界框。在这种情况下,仍然必须选择选择器参数作为边界框选择的后备默认参数;但是,边界框不应忽略此参数:
>>> from astropy.modeling.models import Polynomial2D
>>> from astropy.modeling import bind_compound_bounding_box
>>> model = Polynomial2D(3)
>>> bboxes = {
... 0: ((0, 1), (1, 2)),
... 1: ((2, 3), (3, 4))
... }
>>> selector_args = [('x', False)]
>>> bind_compound_bounding_box(model, bboxes, selector_args, order='F')
>>> model.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='x', ignore=False)
)
)
让用户选择评估的边界框,而不是指定, with_bounding_box=True 作为关键字参数;相反,用户指定 with_bounding_box=<bounding_key> **
>>> model(0.5, 1.5, with_bounding_box=0)
0.0
>>> model(0.5, 1.5, with_bounding_box=1)
nan
忽略边界框中的输入#
两者都有 standard bounding box 和 CompoundBoundingBox 支持忽略边界框强制执行的特定输入。有效地,对于多维模型,可以定义边界框,以便边界仅应用于模型的输入的子集,而不是默认地对每个输入强制某种类型的边界。请注意,使用此功能等同于定义输入的边界 [-np.inf, np.inf] 。
警告
这个 ignored 使用元组和属性接口向模型构建/添加边界框时,输入功能不可用。也就是说,在使用设置边界框时不能忽略输入 model.bounding_box = (-1, 1) 。此功能仅通过方法提供 bind_bounding_box 和 bind_compound_bounding_box 。
忽略边界框的输入可以通过将要忽略的输入名称字符串列表传递给 ignored 任何主边界框接口中的关键字参数。**
>>> from astropy.modeling.models import Polynomial1D
>>> from astropy.modeling import bind_bounding_box
>>> model1 = Polynomial2D(3)
>>> bind_bounding_box(model1, {'x': (-1, 1)}, ignored=['y'])
>>> model1.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='C'
)
>>> model1(-2, 0, with_bounding_box=True)
nan
>>> model1(0, 300, with_bounding_box=True)
0.0
同样,忽略的输入将应用于复合边界框中包含的所有边界框。**
>>> from astropy.modeling import bind_compound_bounding_box
>>> model2 = Polynomial2D(3)
>>> bboxes = {
... 0: {'x': (0, 1)},
... 1: {'x': (1, 2)}
... }
>>> selector_args = [('x', False)]
>>> bind_compound_bounding_box(model2, bboxes, selector_args, ignored=['y'], order='F')
>>> model2.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=1, upper=2)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='x', ignore=False)
)
)
>>> model2(0.5, 300, with_bounding_box=0)
0.0
>>> model2(0.5, 300, with_bounding_box=1)
nan
有效评估 Model.render()#
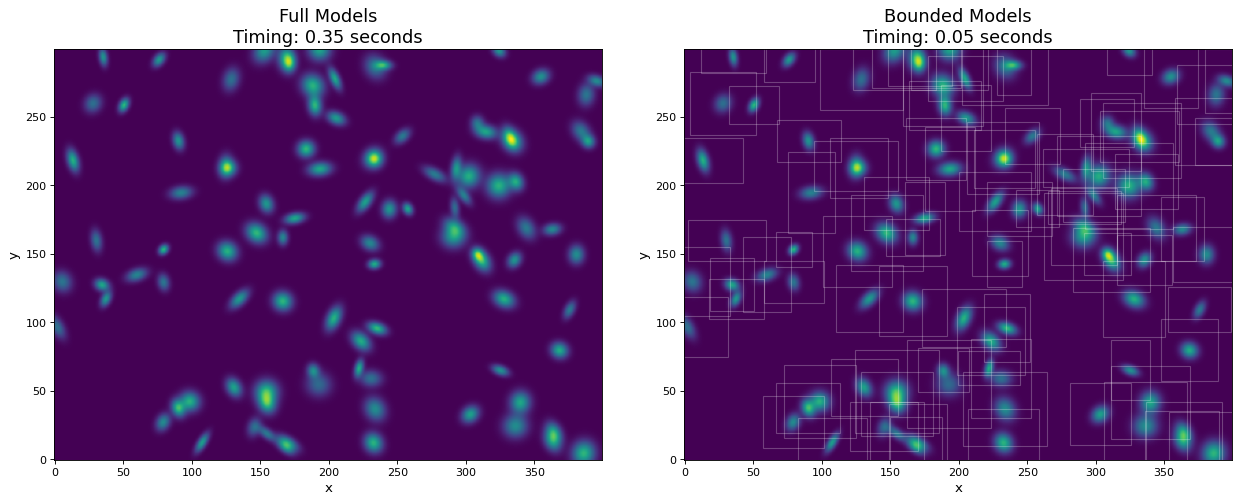
当一个模型在比模型本身大得多的范围内被评估时,使用 Model.render 方法,如果考虑效率。这个 render 方法可用于计算相同维数数组上的模型。 model.render() 可以不带参数调用以返回边框区域的“邮资戳”。
在本例中,我们生成100个2D高斯源的300x400像素图像。为了进行比较,模型在使用和不使用边界框的情况下都进行了评估。通过使用边界框,评估速度提高了大约10倍,而信息损失可以忽略不计。
import numpy as np
from time import time
from astropy.modeling import models
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
imshape = (300, 400)
y, x = np.indices(imshape)
# Generate random source model list
rng = np.random.default_rng(0)
nsrc = 100
model_params = [
dict(amplitude=rng.uniform(.5, 1),
x_mean=rng.uniform(0, imshape[1] - 1),
y_mean=rng.uniform(0, imshape[0] - 1),
x_stddev=rng.uniform(2, 6),
y_stddev=rng.uniform(2, 6),
theta=rng.uniform(0, 2 * np.pi))
for _ in range(nsrc)]
model_list = [models.Gaussian2D(**kwargs) for kwargs in model_params]
# Render models to image using bounding boxes
bb_image = np.zeros(imshape)
t_bb = time()
for model in model_list:
model.render(bb_image)
t_bb = time() - t_bb
# Render models to image using full evaluation
full_image = np.zeros(imshape)
t_full = time()
for model in model_list:
model.bounding_box = None
model.render(full_image)
t_full = time() - t_full
flux = full_image.sum()
diff = (full_image - bb_image)
max_err = diff.max()
# Plots
fig, axs = plt.subplots(figsize=(16, 7), ncols=2)
fig.subplots_adjust(left=.05, right=.97, bottom=.03, top=.97, wspace=0.15)
# Full model image
ax1 = axs[0]
ax1.imshow(full_image, origin='lower')
ax1.set_title(f'Full Models\nTiming: {t_full:.2f} seconds', fontsize=16)
ax1.set(xlabel='x', ylabel='y')
# Bounded model image with boxes overplotted
ax2 = axs[1]
ax2.imshow(bb_image, origin='lower')
for model in model_list:
del model.bounding_box # Reset bounding_box to its default
dy, dx = np.diff(model.bounding_box).flatten()
pos = (model.x_mean.value - dx / 2, model.y_mean.value - dy / 2)
r = Rectangle(pos, dx, dy, edgecolor='w', facecolor='none', alpha=.25)
ax2.add_patch(r)
ax2.set_title(f'Bounded Models\nTiming: {t_bb:.2f} seconds', fontsize=16)
ax2.set(xlabel='x', ylabel='y')
# Difference image
fig2, ax = plt.subplots(figsize=(16, 8))
im = ax.imshow(diff, vmin=-max_err, vmax=max_err)
fig2.colorbar(im, format='%.1e')
ax.set_title(f'Difference Image\nTotal Flux Err = {((flux - np.sum(bb_image)) / flux):.0e}')
ax.set(xlabel='x', ylabel='y')
plt.show()

模型可分性#
简单模型有一个布尔值 Model.separable property. It indicates whether the outputs are independent and is essential for computing the separability of compound models using the is_separable() function. Having a separable compound model means that it can be decomposed into independent models, which in turn is useful in many applications. For example, it may be easier to define inverses using the independent parts of a model than the entire model. In other cases, tools using Generalized World Coordinate System (GWCS) ,可以更灵活地利用可分离的光谱和空间变换。
如果自定义子类 Model needs to override the computation of its separability it can implement the ``_ 计算可分离性_矩阵``方法,该方法应返回该模型的可分离性矩阵。
模型集#
在某些情况下,描述同一类型但具有不同参数值集的许多模型是有用的。这可以简单地通过实例化 Model 根据需要。但对于大量的车型来说,这可能是低效的。为此,所有模型类 astropy.modeling 也可以用来表示模型 set 它是相同类型的模型的集合,但其参数的值不同。
要实例化模型集,请使用参数 n_models=N 在哪里? N 构造模型时集合中的模型数。每个参数的值必须是长度的列表或数组 N ,这样数组中的每个项都对应于集合中的一个模型:
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=[1, 2], mean=[0, 0],
... stddev=[0.1, 0.2], n_models=2)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 2
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 0.1
2.0 0.0 0.2
这相当于两个带参数的高斯函数 amplitude=1, mean=0, stddev=0.1 和 amplitude=2, mean=0, stddev=0.2 分别。打印模型时,参数值显示为表格,每行对应于集合中的单个模型。
模型集中的模型数量可以使用 len 内置:
>>> len(g)
2
单个模型的长度为1,因此不被视为模型集。
评估模型集时,默认情况下,输入的长度必须与模型数相同,每个模型有一个输入:
>>> g([0, 0.1])
array([1. , 1.76499381])
结果是一个数组,集合中每个模型有一个结果。也可以将单个输入值广播到集合中的所有模型:
>>> g(0)
array([1., 2.])
或者当输入是数组时:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]])
>>> print(x)
[[0. 0. 0. ]
[0.1 0.1 0.1]]
>>> g(x)
array([[1. , 1. , 1. ],
[1.76499381, 1.76499381, 1.76499381]])
在内部,输入、输出和参数值的形状由属性控制- model_set_axis . 在上述情况下 model_set_axis=0 ::
>>> g.model_set_axis
0
这表明沿0轴的元素将作为输入传递到各个模型。有时,沿不同轴传递输入可能很有用,例如第一个轴:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]]).T
>>> print(x)
[[0. 0.1]
[0. 0.1]
[0. 0.1]]
因为此模型集中有两个模型,并且我们将沿着第0轴传递三个输入,因此计算将失败:
>>> g(x)
Traceback (most recent call last):
...
ValueError: Input argument 'x' does not have the correct dimensions in
model_set_axis=0 for a model set with n_models=2.
有两种方法可以解决这个问题。 model_set_axis 可以在评估模型时传入::
>>> g(x, model_set_axis=1)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
或者当模型初始化时:
>>> g = models.Gaussian1D(amplitude=[[1, 2]], mean=[[0, 0]],
... stddev=[[0.1, 0.2]], n_models=2,
... model_set_axis=1)
>>> g(x)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
请注意,在后一种情况下,单个参数的形状已更改为2D,因为现在参数是沿着第一个轴定义的。
价值 model_set_axis 是一个整数,表示定义不同参数集和输入的轴,或者是布尔值 False ,在这种情况下,它指示所有模型集在评估时应使用相同的输入。例如,上述模型的值为1 model_set_axis .如果 model_set_axis=False 通过后,将对同一输入评估两个模型:
>>> g.model_set_axis
1
>>> result = g(x, model_set_axis=False)
>>> result
array([[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]]])
>>> result[: , 0]
array([[1. , 0.60653066],
[1. , 0.60653066],
[1. , 0.60653066]])
>>> result[: , 1]
array([[2. , 1.76499381],
[2. , 1.76499381],
[2. , 1.76499381]])
目前,模型集对于拟合一组 线性的 模型 (example )允许将大量相同类型的模型同时(并且彼此独立地)拟合到一些大的输入集,例如将多项式拟合到数据立方体中每个像素的时间响应。这可以大大加快装配过程。加速是由于求解方程组以找到精确解。非线性模型需要迭代算法,目前无法使用模型集进行拟合。非线性模型的模型集只能被评估。
拟合模型集时,数据数组以正确的形状传递给装配工是很重要的。形状取决于 model_set_axis 要拟合的模型的属性。规则是,与模型集相对应的因变量的索引应该沿着 model_set_axis 尺寸。例如,对于包含3个模型的1D模型集 model_set_axis == 1 形状 y 应为(x,3)::
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial1D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(4)
>>> y = np.array([2*x+1, x+4, x]).T
>>> print(y)
[[1 4 0]
[3 5 1]
[5 6 2]
[7 7 3]]
>>> print(y.shape)
(4, 3)
>>> m = Polynomial1D(1, n_models=3, model_set_axis=1)
>>> mfit = fitter(m, x, y)
对于具有3个模型和 model_set_axis = 0 形状 z 应为(3,x,y)::
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial2D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(8).reshape(2, 4)
>>> y = x
>>> z = np.asarray([2 * x + 1, x + 4, x + 3])
>>> print(z.shape)
(3, 2, 4)
>>> m = Polynomial2D(1, n_models=3, model_set_axis=0)
>>> mfit = fitter(m, x, y, z)
模型序列化(将模型写入文件)#
模型可以使用 ASDF 格式。这在许多上下文中都是有用的,其中之一是 Generalized World Coordinate System (GWCS) .
通过将对象分配给 AsdfFile.tree :
>>> from asdf import AsdfFile
>>> from astropy.modeling import models
>>> rotation = models.Rotation2D(angle=23.7)
>>> f = AsdfFile()
>>> f.tree['model'] = rotation
>>> f.write_to('rotation.asdf')
要读取文件并创建模型,请执行以下操作:
>>> import asdf
>>> with asdf.open('rotation.asdf') as f:
... model = f.tree['model']
>>> print(model)
Model: Rotation2D
Inputs: ('x', 'y')
Outputs: ('x', 'y')
Model set size: 1
Parameters:
angle
-----
23.7
复合模型也可以序列化。请注意,某些模型属性(例如 meta , tied 拟合中使用的参数约束)以及模型集尚不可序列化。有关模型序列化的更多信息,请参见 The asdf-astropy Extension Package 。

