洛伦兹1D

class astropy.modeling.functional_models.Lorentz1D(amplitude=1, x_0=0, fwhm=1, **kwargs)

基类：Fittable1DModel

一维洛伦兹模型。

参数:

amplitude : float 或 Quantity 。Python ：浮点或数量。

峰值-对于标准化配置文件(积分为1)，设置振幅=2/(np.pi*fwhm)

x_0 : float 或 Quantity 。Python ：浮点或数量。

峰顶位置

fwhm : float 或 Quantity 。Python ：浮点或数量。

半最大全宽（FWHM）

其他参数:

fixed : dict ，可选Python：Dict，可选

字典 {{parameter_name: boolean}} 在拟合过程中不能改变的参数。True表示参数保持不变。或者 fixed 可以使用参数的属性。

tied : dict ，可选Python：Dict，可选

字典 {{parameter_name: callable}} 链接到其他参数的参数。字典值是提供链接关系的可调用项。或者 tied 可以使用参数的属性。

bounds : dict ，可选Python：Dict，可选

字典 {{parameter_name: value}} 参数的上下界。键是参数名。值是一个长度为2的列表或元组，为参数提供所需的范围。或者 min 和 max 可以使用参数的属性。

eqcons : list ，可选Python：列表，可选

长度函数列表 n 这样的话 eqcons[j](x0,*args) == 0.0 在一个成功优化的问题中。

ineqcons : list ，可选Python：列表，可选

长度函数列表 n 这样的话 ieqcons[j](x0,*args) >= 0.0 是一个成功优化的问题。

参见

Gaussian1D, Box1D, RickerWavelet1D

笔记

全部输入或不输入 x ，位置 x_0 和 fwhm 必须一致地使用兼容的单位或作为无单位数字提供。

模型公式：

\[f（x）=\frac{A\gamma^{2}}{\gamma^{2}+\左（x-x{0}\右）^{2}}}\]

在哪里？ \(\gamma\) 是给定半高宽的一半。

实例

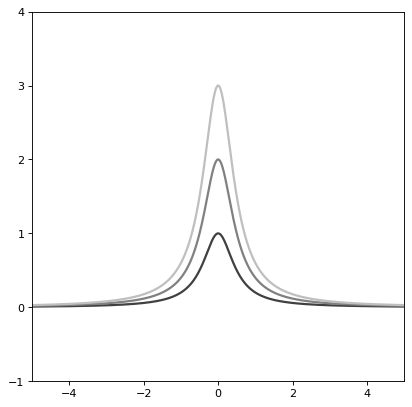
import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import Lorentz1D

plt.figure()
s1 = Lorentz1D()
r = np.arange(-5, 5, .01)

for factor in range(1, 4):
    s1.amplitude = factor
    plt.plot(r, s1(r), color=str(0.25 * factor), lw=2)

plt.axis([-5, 5, -1, 4])
plt.show()

(png, svg, pdf)

属性摘要

amplitude
fwhm
input_units	此属性用于指示evaluate方法所需的单元或单元集，并返回将输入映射到单元（或 None 如果接受任何单位）。
param_names	描述此类型模型的参数的名称。
x_0

方法总结

evaluate(x, amplitude, x_0, fwhm)	一维洛伦兹模型函数。
fit_deriv(x, amplitude, x_0, fwhm)	一维洛伦兹模型对参数的导数。

属性文档

amplitude = Parameter('amplitude', value=1.0)

fwhm = Parameter('fwhm', value=1.0)

input_units

param_names = ('amplitude', 'x_0', 'fwhm')

描述此类型模型的参数的名称。

此元组中的参数与初始化特定类型的模型时应传入的顺序相同。某些类型的模型，如多项式模型，根据模型的某些其他属性（如阶数）有不同数量的参数。

定义自定义模型类时，此属性的值由 Parameter 在类中定义的body属性。

x_0 = Parameter('x_0', value=0.0)

方法文件

static evaluate(x, amplitude, x_0, fwhm)

一维洛伦兹模型函数。

static fit_deriv(x, amplitude, x_0, fwhm)

一维洛伦兹模型对参数的导数。