傅里叶级数#
提供计算傅立叶级数的方法。
- class sympy.series.fourier.FourierSeries(*args)[源代码]#
表示傅里叶正弦/余弦级数。
解释
此类仅表示傅立叶级数。不执行计算。
有关如何计算傅立叶级数,请参见
fourier_series()文档字符串。- scale(s)[源代码]#
用与x无关的项来缩放函数。
解释
f(x)->s*f(x)
如果已经计算出f(x)的傅立叶级数,这是很快的。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x**2, (x, -pi, pi)) >>> s.scale(2).truncate() -8*cos(x) + 2*cos(2*x) + 2*pi**2/3
- scalex(s)[源代码]#
用一个与x无关的项来缩放x。
解释
f(x)->f(s*x)
如果已经计算出f(x)的傅立叶级数,这是很快的。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x**2, (x, -pi, pi)) >>> s.scalex(2).truncate() -4*cos(2*x) + cos(4*x) + pi**2/3
- shift(s)[源代码]#
将函数移动一个与x无关的项。
解释
f(x)->f(x)+s
如果已经计算出f(x)的傅立叶级数,这是很快的。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x**2, (x, -pi, pi)) >>> s.shift(1).truncate() -4*cos(x) + cos(2*x) + 1 + pi**2/3
- shiftx(s)[源代码]#
将x移动一个与x无关的项。
解释
f(x)->f(x+s)
如果已经计算出f(x)的傅立叶级数,这是很快的。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x**2, (x, -pi, pi)) >>> s.shiftx(1).truncate() -4*cos(x + 1) + cos(2*x + 2) + pi**2/3
- sigma_approximation(n=3)[源代码]#
返回 \(\sigma\) -关于n阶Fourier级数的逼近。
- 参数:
n :内景
近似中考虑的最高阶项。
- 返回:
Expr :
函数展开为Fourier级数的Sigma逼近。
解释
西格玛近似调整傅里叶求和,以消除吉布斯现象,否则将发生在不连续。T周期函数的Fourier级数的sigma近似求和可以写成
\[s(\theta)=\frac{1}{2}a_0+\sum{k=1}^{m-1}\]在哪里? \(a_0, a_k, b_k, k=1,\ldots,{{m-1}}\) 是标准傅里叶级数系数和 \(\operatorname{{sinc}} \Bigl( \frac{{k}}{{m}} \Bigr)\) 是兰佐斯人吗 \(\sigma\) 因子(用标准化表示 \(\operatorname{{sinc}}\) 函数)。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x, (x, -pi, pi)) >>> s.sigma_approximation(4) 2*sin(x)*sinc(pi/4) - 2*sin(2*x)/pi + 2*sin(3*x)*sinc(3*pi/4)/3
笔记
行为
sigma_approximation()不同于truncate()-它接受所有小于n阶的非零项,而不是前n个非零项。工具书类
- truncate(n=3)[源代码]#
返回序列的前n个非零项。
If
nis None return an iterator.- 参数:
n :int或None
近似或无非零项的数量。
- 返回:
Expr or iterator :
函数的逼近展开成傅立叶级数。
实例
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> s = fourier_series(x, (x, -pi, pi)) >>> s.truncate(4) 2*sin(x) - sin(2*x) + 2*sin(3*x)/3 - sin(4*x)/2
- sympy.series.fourier.fourier_series(f, limits=None, finite=True)[源代码]#
计算傅里叶三角级数展开式。
- 参数:
限制 :(sym,start,end),可选
sym 表示计算序列所依据的符号。
开始 和 end 表示傅里叶级数收敛到给定函数的区间的起点和终点。
默认范围指定为\(-\pi\)和\(\pi\)。
- 返回:
FourierSeries
表示傅里叶三角级数的符号对象。
解释
在区间\((a,b)\)上,\(f(x)\)的傅里叶三角级数定义为:
\[\分形{a0}{2}+\sum{n=1}^{\infty}\]其中系数为:
\[L=b-a\]\[a{0=\frac{2}{L}\int{a}^{b}{f(x)dx}\]\[a{n=\frac{2}{L}\int{a}^{b}{f(x)\cos(\frac{2n\pix}{L})dx}\]\[b{n=\frac{2}{L}\int{a}^{b}{f(x)\sin(\frac{2n\pix}{L})dx}\]给定的函数\(f(x)\)是否为周期性的条件是非常必要的,因为它足以考虑级数只在给定的区间内收敛到\(f(x)\),而不是整个实线。
This also brings a lot of ease for the computation because you do not have to make \(f(x)\) artificially periodic by wrapping it with piecewise, modulo operations, but you can shape the function to look like the desired periodic function only in the interval \((a, b)\), and the computed series will automatically become the series of the periodic version of \(f(x)\).
此属性在下面的示例部分中进行了说明。
实例
计算\(f(x)=x^2\)的傅立叶级数:
>>> from sympy import fourier_series, pi >>> from sympy.abc import x >>> f = x**2 >>> s = fourier_series(f, (x, -pi, pi)) >>> s1 = s.truncate(n=3) >>> s1 -4*cos(x) + cos(2*x) + pi**2/3
傅里叶级数的移位:
>>> s.shift(1).truncate() -4*cos(x) + cos(2*x) + 1 + pi**2/3 >>> s.shiftx(1).truncate() -4*cos(x + 1) + cos(2*x + 2) + pi**2/3
傅里叶级数的标度:
>>> s.scale(2).truncate() -8*cos(x) + 2*cos(2*x) + 2*pi**2/3 >>> s.scalex(2).truncate() -4*cos(2*x) + cos(4*x) + pi**2/3
计算\(f(x)=x\)的傅立叶级数:
这说明了如何截断到更高的阶数可以获得更好的收敛性。
>>> from sympy import fourier_series, pi, plot >>> from sympy.abc import x >>> f = x >>> s = fourier_series(f, (x, -pi, pi)) >>> s1 = s.truncate(n = 3) >>> s2 = s.truncate(n = 5) >>> s3 = s.truncate(n = 7) >>> p = plot(f, s1, s2, s3, (x, -pi, pi), show=False, legend=True)
>>> p[0].line_color = (0, 0, 0) >>> p[0].label = 'x' >>> p[1].line_color = (0.7, 0.7, 0.7) >>> p[1].label = 'n=3' >>> p[2].line_color = (0.5, 0.5, 0.5) >>> p[2].label = 'n=5' >>> p[3].line_color = (0.3, 0.3, 0.3) >>> p[3].label = 'n=7'
>>> p.show()
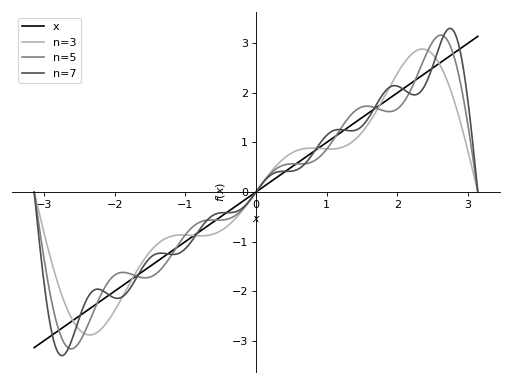
这说明了如果指定了不同的范围,序列如何收敛到不同的锯齿波。
>>> s1 = fourier_series(x, (x, -1, 1)).truncate(10) >>> s2 = fourier_series(x, (x, -pi, pi)).truncate(10) >>> s3 = fourier_series(x, (x, 0, 1)).truncate(10) >>> p = plot(x, s1, s2, s3, (x, -5, 5), show=False, legend=True)
>>> p[0].line_color = (0, 0, 0) >>> p[0].label = 'x' >>> p[1].line_color = (0.7, 0.7, 0.7) >>> p[1].label = '[-1, 1]' >>> p[2].line_color = (0.5, 0.5, 0.5) >>> p[2].label = '[-pi, pi]' >>> p[3].line_color = (0.3, 0.3, 0.3) >>> p[3].label = '[0, 1]'
>>> p.show()
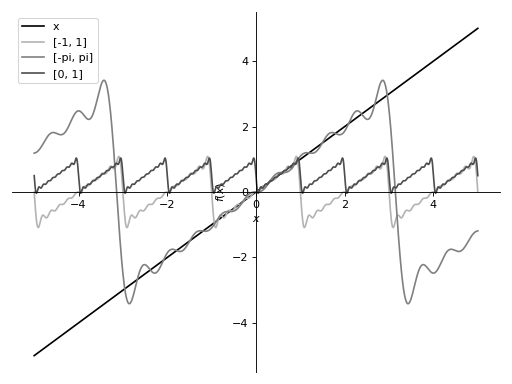
笔记
由于在计算an,bn时需要积分,计算Fourier级数可能很慢。
通过对已经计算出的傅立叶级数进行移位和缩放来计算函数的傅立叶级数比重新计算要快得多。
e、 g.如果
x**2已知的傅里叶级数x**2 - 1可以通过移动-1.工具书类