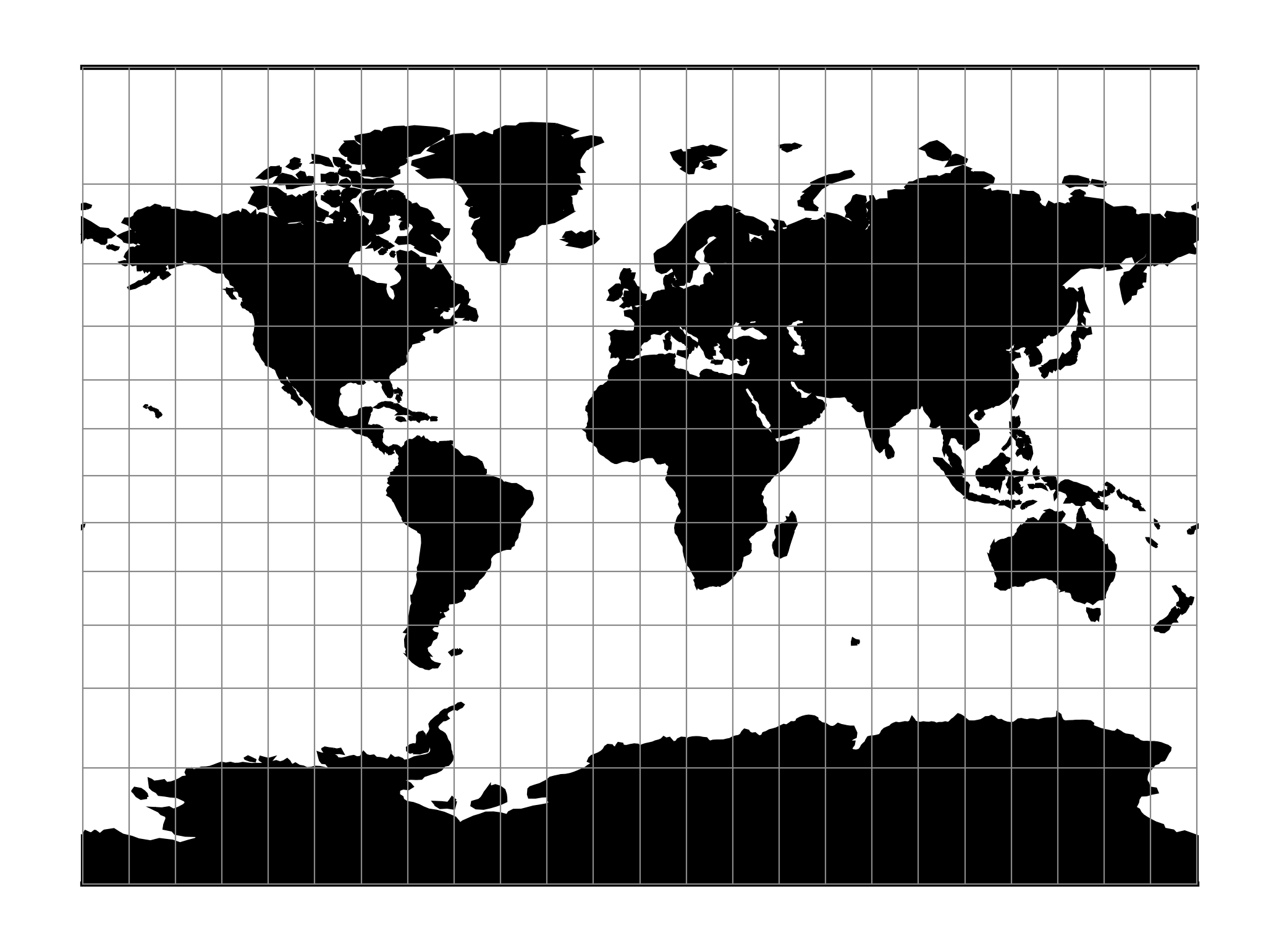
米勒圆柱¶
米勒圆柱投影是奥斯本·梅特兰·米勒于1942年提出的一种改进的墨卡托投影。纬度的比例是 \(\frac{{4}}{{5}}\) ,根据墨卡托投影,然后将结果乘以 \(\frac{{5}}{{4}}\) 保持赤道的尺度。
Classification |
既不是保形的也不是等面积的圆柱形 |
可用表格 |
正逆球面 |
限定区域 |
全球,但最好在赤道附近使用 |
Alias |
磨坊 |
Domain |
二维 |
输入类型 |
大地坐标 |
输出类型 |
投影坐标 |
项目字符串: +proj=mill¶
使用¶
米勒圆柱投影用于世界地图和一些地图集,包括美国国家地图集(美国地质勘探局,1970年,第330-331页) [Snyder1987] .
使用中央子午线90°W的示例:
$ echo -100 35 | proj +proj=mill +lon_0=90w
-1113194.91 4061217.24
参数¶
备注
投影的所有参数都是可选的。
- +lon_0=<value>¶
投影中心的经度。
默认为0.0。
- +x_0=<value>¶
假东距。
默认为0.0。
- +y_0=<value>¶
假北距。
默认为0.0。
数学定义¶
描述米勒投影的公式都取自 [Snyder1987] .
正向投影¶
\[x=\λ\]
\[y=1.25 * \ln \left[ \tan \left(\frac{{\pi}}{{4}} + 0.4 * \phi\右)\right]\]
反投影¶
\[\λ=x\]
\[\Phi=2.5 * ( \arctan \left[ e^{{0.8 * Y}\右]-\FRAC{\pi}{4})\]