墨卡托

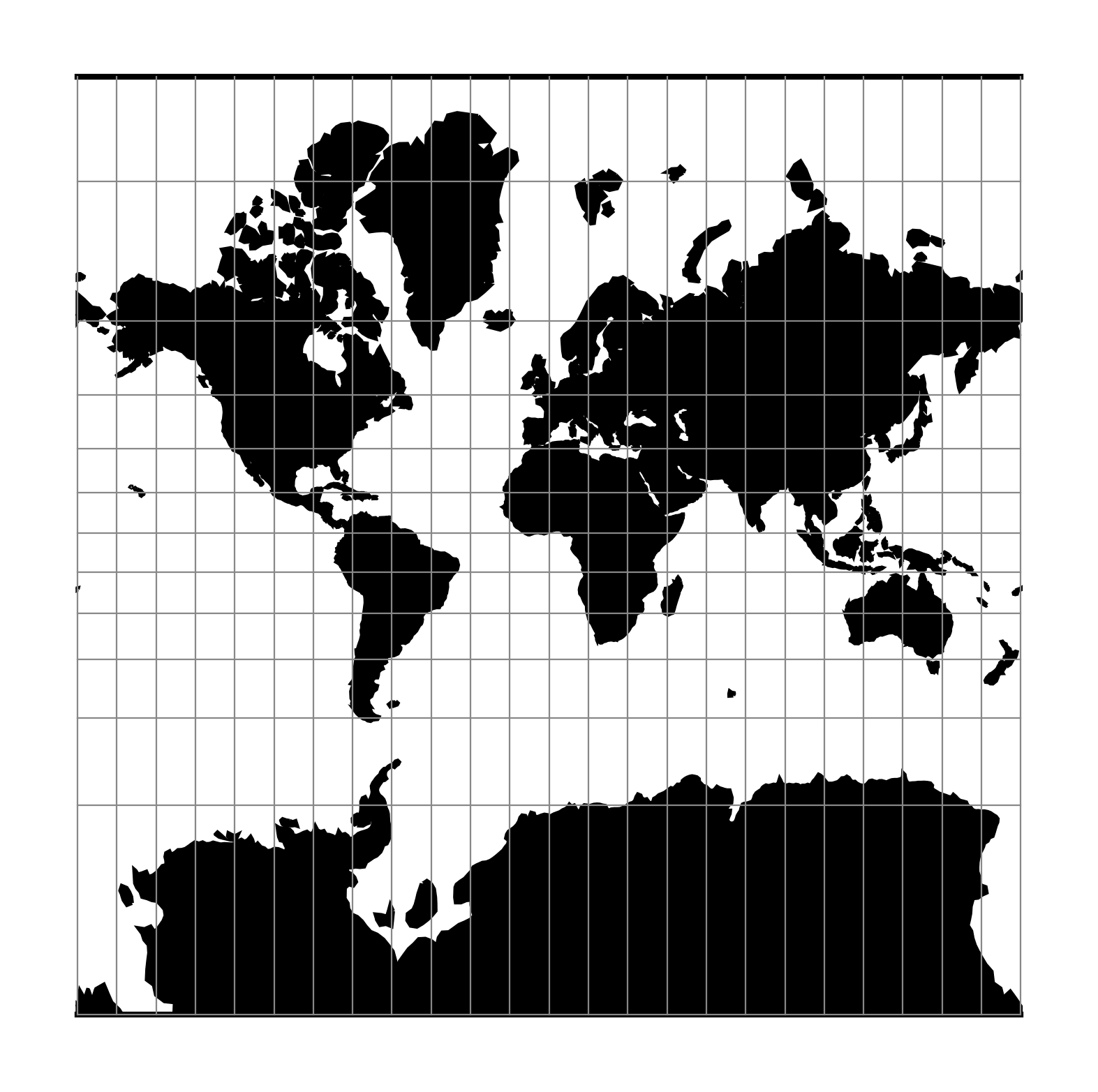
墨卡托投影是起源于16世纪的圆柱形地图投影。它被广泛认为是第一个经常使用的地图投影。它是一种共形投影，其中赤道以恒定的比例投影到一条直线上。投影的性质是一条等角线，一条恒定航向的路线，投影到一条直线上。这使得它适合于航海目的。

Classification	共形圆柱
可用表格	正向和反向，球形和椭圆形
限定区域	全球，但最好在赤道附近使用
Alias	默克
Domain	二维
输入类型	大地坐标
输出类型	投影坐标

项目字符串： +proj=merc

使用

应用应限于赤道地区，但通常用于具有真实比例尺纬度的航海图 (+lat_ts )在图表边界内或附近指定。它被认为不适合用于世界地图，因为面积严重扭曲；例如，格陵兰岛的投影面积大于南美洲，尽管格陵兰岛的面积很小 \(\frac18\) 南美洲的 [Snyder1987] .

使用真实比例纬度的示例：

$ echo 56.35 12.32 | proj +proj=merc +lat_ts=56.5
3470306.37    759599.90

使用比例因子的示例：

echo 56.35 12.32 | proj +proj=merc +k_0=2
12545706.61     2746073.80

注意 +lat_ts 和 +k_0 相互排斥。如果一起使用， +lat_ts 优先于 +k_0 .

参数

备注

投影的所有参数都是可选的。

+lat_ts=<value>

真实尺度的纬度。定义缩放不扭曲的纬度。优先于 +k_0 如果两个选项一起使用。

默认为0.0。

+k_0=<value>

比例因子。确定投影中使用的比例因子。

默认为1.0。

+lon_0=<value>

投影中心的经度。

默认为0.0。

+x_0=<value>

假东距。

默认为0.0。

+y_0=<value>

假北距。

默认为0.0。

+ellps=<value>

内置椭球体定义的名称。

看见 椭球体 获取更多信息，或执行 proj -le 以获取内置椭圆体名称的列表。

默认为“GRS80”。

+R=<value>

球体的半径，以米为单位。如果与一起使用 +ellps ， +R 优先。

看见 椭球体尺寸参数 了解更多信息。

数学定义

球形

对于投影的球形形式，我们引入比例因子：

\[k\u 0=\cos\phi{ts}\]

正向投影

\[x=k\u 0R\lambda；\qquad y=k\u 0R\psi\]

\[\begin{split}\psi&=\ln\tan\biggl（\frac{\pi}{4}+\frac{\phi}{2}\biggr）\\\end{split}\]

数量 \(\psi\) 是等轴测纬度。

反投影

\[\lambda=\frac{x}{k\u 0R}；\qquad\psi=\frac{y}{k\u 0R}\]

\[\begin{split}\φ&=\frac{\pi}{2}-2\tan^{-1}\exp（-\psi）\\\end{split}\]

椭球形

对于投影的椭球形式，我们引入比例因子：

\[k\u 0=m（\phi{ts}）\]

在哪里？

\[m（\phi）=\frac{\cos\phi}{\sqrt{1-e^2\sin^2\phi}}\]

\(a\,m(\phi)\) 圆的半径是纬度 \(\phi\) .

正向投影

\[x=k\u 0 a\lambda；\qquad y=k\u 0 a\psi\]

\[\psi&=\ln\tan\biggl（\frac\pi4+\frac{\phi}2\biggr）\]

反投影

\[\lambda=\frac{x}{k\u 0 a}；\quad\psi=\frac{y}{k\u 0 a}\]

纬度 \(\phi\) 通过将 \(\psi\) . 这遵循下面给出的方法 [Karney2011tm] . 首先介绍共形纬度

\[\chi=\tan^{-1}\sinh\psi\]

纬度的切线 \(\tau = \tan\phi\) 和 \(\tau' = \tan\chi = \sinh\psi\) 与…有关

\[\tau'=\tau\sqrt{1+\sigma^2}-\sigma\sqrt{1+\tau^2}\]

在哪里？

\[\西格玛=\sinh\bigl（e\tanh^{-1}（e\tau/\sqrt{1+\tau^2}）\bigr）\]

这是通过取 \(\sinh\) 方程的 \(\psi\) 使用多参数公式。方程 \(\tau'\) 可以解决给 \(\tau\) 用牛顿法 \(\tau = \tau'/(1 - e^2)\) 作为一个初步的猜测和所需的衍生工具，由

\[\frac{d\tau‘}{d\tau}=\frac{1-e^2}{1+(1-e^2)\tau^2} \sqrt{1+\tau^2}\sqrt{1+\tau^2}\]

这在不超过2次迭代之后收敛。最终设定 \(\phi=\tan^{{-1}}\tau\) .

进一步阅读

1. Wikipedia

2. Wolfram Mathworld