胆(胆立体图)¶
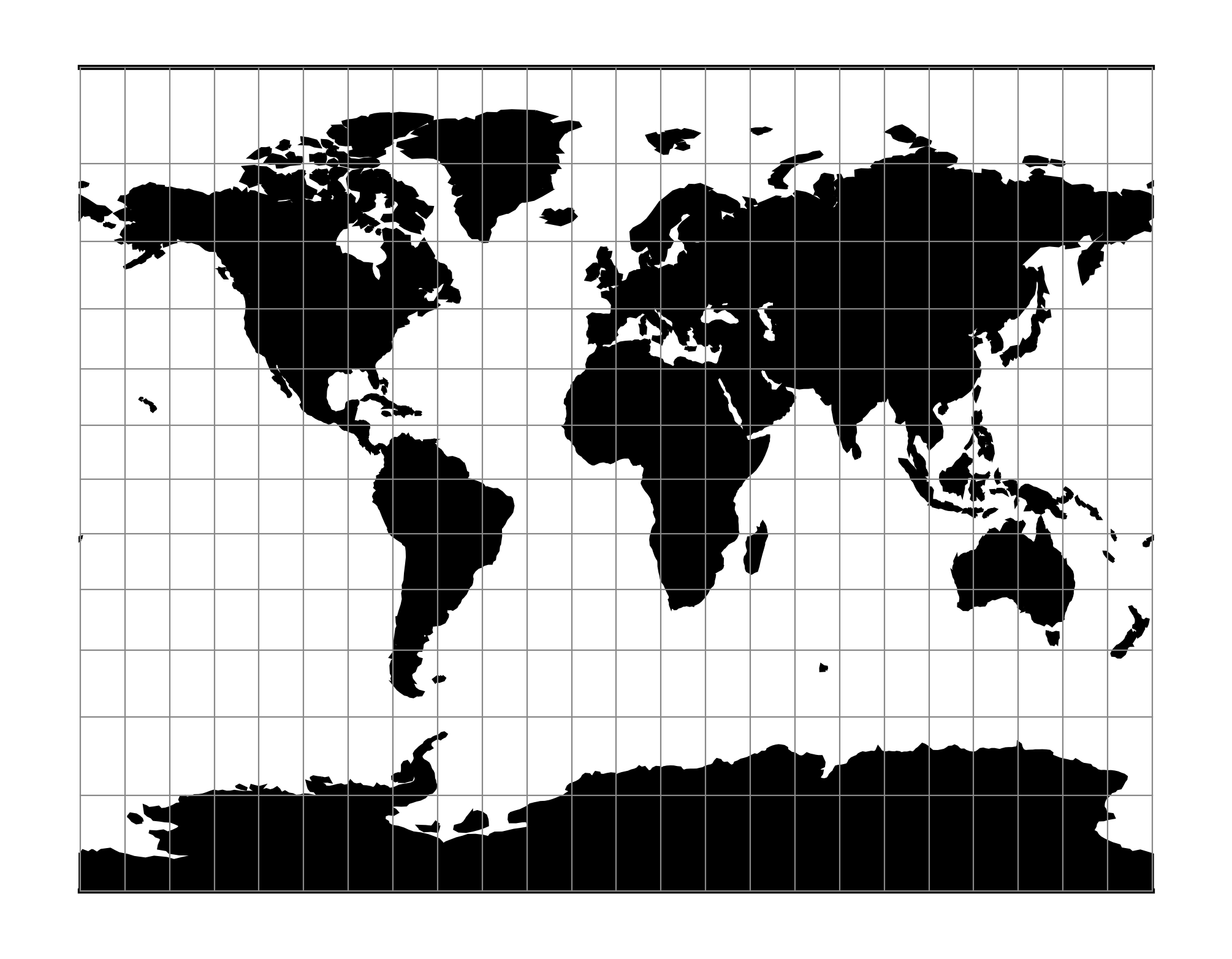
Gall赤平投影是由jamesgall于1855年提出的一种柱面投影。它既不是等面积的,也不是共形的,而是试图平衡任何投影中固有的失真。
Classification |
横斜圆柱 |
可用表格 |
正向和反向,球形 |
限定区域 |
全球的 |
Alias |
胆 |
Domain |
二维 |
输入类型 |
大地坐标 |
输出类型 |
投影坐标 |
项目字符串: +proj=gall¶
使用¶
对世界地图的需要避免了墨卡托投影的某些比例的夸张,这导致了一些常用的圆柱形修改,以及其他非圆柱形的修改。最早常见的圆柱形例子是由爱丁堡的詹姆斯加尔于1855年发明的(加尔,1885年,第119-123页)。他的子午线是等间距的,但是平行线的间距在远离赤道的地方越来越大。纬度的平行线实际上被投射到一个包裹在球体上的圆柱体上,但在纬度处被切割。45°N和S,透视点是赤道上与被投影子午线相对的点。它被用于英国的一些地图集,但很少在美国。胆囊投影既不是保形的,也不是等面积的,而是多种特征的融合。与墨卡托不同的是,五倍子将两极显示为横穿地图顶部和底部的线条。
备注
不能将盖尔投影与盖尔-彼得斯投影混淆,后者是 等面积圆柱形 。
使用Gall立体投影的示例::
$ echo 9 51 | proj +proj=gall +lon_0=0 +x_0=0 +y_0=0 +ellps=WGS84 +units=m
708432.90 5193386.36
使用Gall立体成像(中央子午线90°W)的示例:
$ echo 9 51 | proj +proj=gall +lon_0=90w +x_0=0 +y_0=0 +ellps=WGS84 +units=m
7792761.91 5193386.36
参数¶
备注
投影的所有参数都是可选的。
- +lon_0=<value>¶
投影中心的经度。
默认为0.0。
- +x_0=<value>¶
假东距。
默认为0.0。
- +y_0=<value>¶
假北距。
默认为0.0。
数学定义¶
描述Gall赤平的公式都取自 [Snyder1993] 。
球形¶
正向投影¶
\[x=\frac{\lambda}{\sqrt{2}}\]
\[y=(1+\frac{\sqrt{2}}{2})\tan(\phi/2)\]
反投影¶
\[\phi=2\arctan(\frac{y}{1+\frac{\sqrt{2}}{2}})\]
\[\λ=\sqrt{2}x\]