斜墨卡托¶
斜墨卡托投影是一种圆柱形地图投影,它闭合了墨卡托投影和横向墨卡托投影之间的间隙。
Classification |
共形圆柱 |
可用表格 |
正向和反向,球形和椭圆形 |
限定区域 |
全局,但仅在倾斜中心线的15度范围内合理准确 |
Alias |
奥梅克 |
Domain |
二维 |
输入类型 |
大地坐标 |
输出类型 |
投影坐标 |
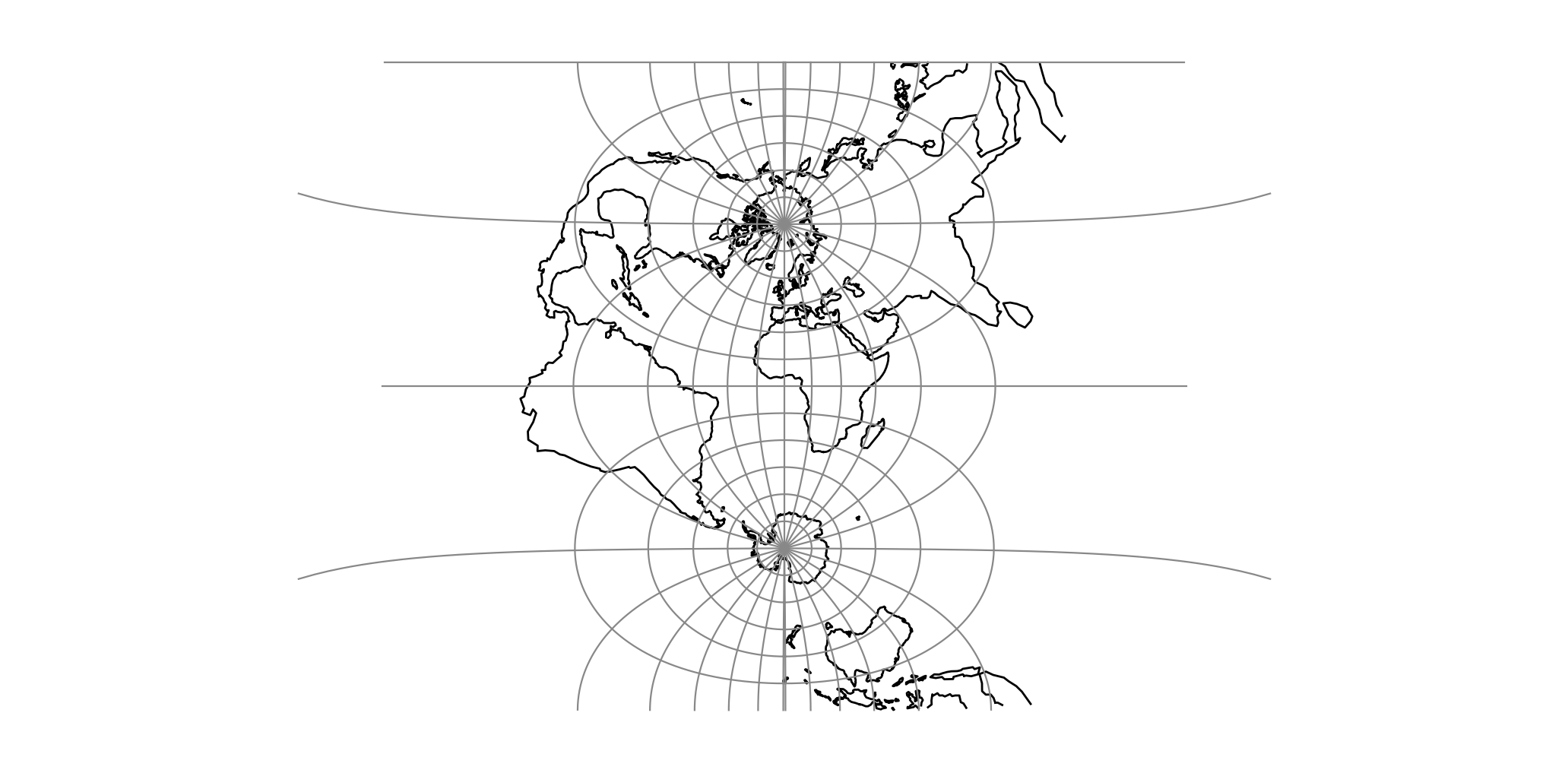
项目字符串: +proj=omerc +lat_1=45 +lat_2=55¶
形象地说,用于展开墨卡托投影的圆柱体沿着赤道接触行星,而横轴墨卡托的圆柱体沿着子午线接触行星,即沿着垂直于赤道的线。
然而,倾斜墨卡托的圆柱体沿着与赤道成任意角度的直线与行星接触。因此,斜墨卡托投影有助于绘制沿既不是南北方向也不是东西方向的最大范围的区域。
墨卡托投影和横轴墨卡托投影都是斜轴墨卡托投影的极限形式:墨卡托投影相当于中心线沿赤道的斜轴墨卡托投影,横轴墨卡托投影相当于中心线沿子午线的斜轴墨卡托投影。
对于球体,斜墨卡托投影的构造可以想象为“倾斜平面墨卡托投影的圆柱体”,因此圆柱体不接触赤道,而是接触球体上任意一个大圆。大圆是由中心线的倾斜角度来定义的,因此把陆地块放在地图中心附近的那个大圆上,在普通墨卡托情况下,赤道就在这个大圆上。
由霍廷开发,斯奈德完善的椭球壳 [Snyder1987] 更为复杂的是,首先从椭球体投影到另一曲面,即“顶点球”,然后从顶点球投影到斜uv平面,最后将斜uv平面校正到地图XY平面。
使用¶
中心线的倾斜角(方位角)可以用两种不同的方式给出。在第一种情况下,使用选项直接给出方位角 +alpha 使用选项定义投影中心 +lonc 和 +lat_0 . 在第二种情况下,通过使用选项在中心线上指定两个点间接给出方位角 +lat_1 , +lon_1 , +lat_2 和 +lon_2 .
示例:验证墨卡托投影是斜角墨卡托投影的极限形式
$ echo 12 55 | proj +proj=merc +ellps=GRS80
1335833.89 7326837.71
$ echo 12 55 | proj +proj=omerc +lonc=0 +alpha=90 +ellps=GRS80
1335833.89 7326837.71
示例:第二种情况-间接给定方位角
$ echo 12 55 | proj +proj=omerc +lon_1=-1 +lat_1=1 +lon_2=0 +lat_2=0 +ellps=GRS80
349567.57 6839490.50
例如:丹麦“系统34”的近似值 [Rittri2012]
$ echo 10.536498003 56.229892362 | proj +proj=omerc +axis=wnu +lonc=9.46 +lat_0=56.13333333 +x_0=-266906.229 +y_0=189617.957 +k=0.9999537 +alpha=-0.76324 +gamma=0 +ellps=GRS80
200000.13 199999.89
输入坐标表示系统34基准点“Agri Bavnehoj”,坐标定义为(200000,200000)。所以在基准点,近似值偏离了17厘米。此用例表示从旧的、稍微错位的基准上的圆柱体投影到现代基准上的类似投影的基准偏移。
参数¶
中心点方位法¶
- +lonc=<value>¶
中心点的经度。
- +lat_0=<value>¶
中心点的纬度。
两点法¶
- +lon_1=<value>¶
第一点的经度。
- +lat_1=<value>¶
第一点的纬度。
- +lon_2=<value>¶
第二点的经度。
- +lat_2=<value>¶
第二点的纬度。
可选的¶
- +no_rot¶
没有纠正(不是“没有旋转”作为一个很好的假设)。不要执行从“扭曲uv平面”(skew uv plane)到“贴图XY平面”(map XY plane)的最后一步。
备注
这一选择可能只是有点用处,但由于(主要)历史原因仍然存在。
- +no_off¶
不要将原点偏移到投影中心。
- +k_0=<value>¶
比例因子。确定投影中使用的比例因子。
默认为1.0。
- +lon_0=<value>¶
投影中心的经度。
默认为0.0。
- +x_0=<value>¶
假东距。
默认为0.0。
- +y_0=<value>¶
假北距。
默认为0.0。