摘要: 在三角形中有一些特殊的三角形,比如:等腰三角形,等边三角形,锐角三角形等等。当然还有我们要说的直角三角形。直角三角形在三角形中是比较特殊的一个三角形,它有一个角是90度,两条边是互相垂直的。除了这些我们还有哪些不知道的呢?我们又如何去判断这个三角形是否是直角三...
在三角形中有一些特殊的三角形,比如:等腰三角形,等边三角形,锐角三角形等等。当然还有我们要说的直角三角形。直角三角形在三角形中是比较特殊的一个三角形,它有一个角是90度,两条边是互相垂直的。除了这些我们还有哪些不知道的呢?我们又如何去判断这个三角形是否是直角三角形呢?
1、判断三角形的办法:
①、有一个角是直角的三角形即是直角三角形。
②、如果三角形的三条边分别为a,b,c,并且a2+b2=c2,则这个三角式就是以c为斜边的直角三角形。
③、两个角互余的三角形也是直角三角形。
④、若两直线相交且它们的斜率之积互为负倒数,则两直线互相垂直。那么这个三角形为直角三角形。
⑤、如果三角形的一个角为30度,而且这个角所对应的那条边是某条边的一半,那么这个三角形就是直角三角形。
⑥、若两直线相交且它们的斜率之积互为负倒数,则两直线互相垂直。那么这个三角形为直角三角形。
2、直角三角形是特殊的三角形,它除了有一般三角形的性质外,还有哪些性质(如图):
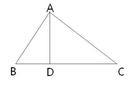
①、直角三角形的两直角边的平方和等于斜边的平方。∠BAC=90°,则AB2+AC2=BC2。
②、直角三角形另外两个角互余。若∠BAC=90°,则∠B+∠C=90°。
③、直角三角形中斜边上的中线等于斜边的二分之一。
④、直角三角形两直角边相乘与斜边和斜边上的高相乘相等。
⑤、如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
AD²=BD·DC。
AB²=BD·BC。
AC²=CD·BC。
⑥、直角三角形中有一个角是30度,那么这个角所对应的边等于斜边的一半。反之也成立。
⑦、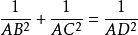 。
。
⑧、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
这些就是几何中的直角三角形的一些性质定理以及判断方法。
