置信区间的计算步骤

置信区间

指由样本统计量所构造的总体参数的估计区间。

在统计学中，一个概率样本的置信区间是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的是被测量参数的测量值的可信程度，即前面所要求的“一定概率”。这个概率被称为置信水平。

举例

如果在一次大选中某人的支持率为55%，而置信水平0.95上的置信区间是（50%,60%），那么他的真实支持率有百分之九十五的机率落在50%和60%之间。

如例子中一样，置信水平一般用百分比表示，因此置信水平0.95上的置信空间也可以表达为：95%置信区间。

置信区间的两端被称为置信极限。对一个给定情形的估计来说，置信水平越高，所对应的置信区间就会越大。

90%置信区间：当给出某个估计值的90%置信区间为【a,b】时,可以理解为我们有90%的信心可以说样本的平均值介于a到b之间,而发生错误的概率为10%.

计算步骤

第一步：求一个样本的均值

第二步：计算出抽样误差。

人们经过实践，通常认为调查:

100个样本的抽样误差为±10%；

500个样本的抽样误差为±5%；

1,200个样本时的抽样误差为±3%；

第三步：用第一步求出的“样本均值”加、减第二步计算的“抽样误差”，得出置信区间的两个端点。

置信区间涵义

设总体X~N(\(μ,σ^2)\)),σ^2已知，μ未知，（X₁……，X_n）为来自X的样本。

样本均值X₀是μ的最大似然估计，从X₀出发考虑一个样本与未知参数μ的函数

U=(X₀-μ)/(σ/√n)

它不包含其他未知参数，并且它的分布已知，U=(X₀-μ)/(σ/√n)~N(0,1),因而它是一个枢轴量。

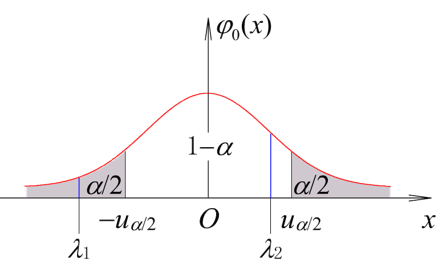
可确定置信下限λ1和置信上限λ2，一般选取-μ_α/2为λ1，μ_α/2为λ2.