scipy.interpolate.splrep

scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, task=0, s=None, t=None, full_output=0, per=0, quiet=1)

查找一维曲线的B样条表示。

在给定数据点集合的情况下 (x[i], y[i]) 确定区间上k次光滑样条逼近 xb <= x <= xe 。

参数

x, yarray_like

定义曲线y=f(X)的数据点。

wARRAY_LIKE，可选

与x和y长度相同的严格正秩-1权数组。这些权值用于计算加权最小二乘样条拟合。如果y值中的误差具有由矢量d给出的标准偏差，则w应为1/d。默认值为1(len(X))。

xb、xe浮动，可选

适合的间隔。如果没有，则默认为x [0] 和x [-1] 分别为。

k整型，可选

样条曲线的拟合程度。建议使用三次样条曲线。应避免偶数的k值，特别是s值较小的情况下。1<=k<=5

task{1，0，-1}，可选

如果TASK==0，则找出给定平滑因子s的t和c。

如果TASK==1，则为平滑因子s的另一个值找到t和c。对于同一组数据，必须存在先前调用TASK=0或TASK=1的情况(t将在内部存储和使用)

如果TASK=-1，找到给定节点集t的加权最小二乘样条曲线。这些节点应该是内部节点，因为末端的节点将自动添加。

s浮动，可选

一种平稳的状态。平滑度的大小通过满足以下条件来确定：SUM((w * (y - g))* 2,axis=0) <= s where g(x) is the smoothed interpolation of (x,y). The user can use s to control the tradeoff between closeness and smoothness of fit. Larger s means more smoothing while smaller values of s indicate less smoothing. Recommended values of s depend on the weights, w. If the weights represent the inverse of the standard-deviation of y, then a good s value should be found in the range (m-sqrt(2 m)，m+sqrt(2 m)) where m is the number of datapoints in x, y, and w. default : s=m-sqrt(2 m)如果提供了权重。如果未提供权重，则S=0.0(插值)。

tARRAY_LIKE，可选

任务所需的节点=-1。如果给定，则任务自动设置为-1。

full_output布尔值，可选

如果非零，则返回可选输出。

per布尔值，可选

如果非零，则认为数据点是周期为x的周期性数据点。 [m-1] -x [0] 并返回光滑的周期样条逼近。y的值 [m-1] 和w [m-1] 都没有用过。

quiet布尔值，可选

非零表示隐藏消息。此参数已弃用；请改用标准Python警告筛选器。

退货

tck元组

包含节点向量、B样条系数和样条曲线阶数的元组(t，c，k)。

fp数组，可选

样条近似的残差平方加权和。

ier整型，可选

关于拆分成功的整数标志。如果ier<=0，则表示成功。如果在以下位置 [1，2，3] 出现错误，但未引发。否则将引发错误。

msg字符串，可选

对应于整数标志Ier的消息。

参见

UnivariateSpline, BivariateSpline

splprep, splev, sproot, spalde, splint

bisplrep, bisplev

BSpline

make_interp_spline

注意事项

看见 splev 用于计算样条及其导数。使用FORTRAN例程 curfit 来自FITPACK。

用户负责确保 x 都是独一无二的。否则， splrep 不会返回合理的结果。

如果提供，则结 t 必须满足勋伯格-惠特尼条件，即必须存在数据点的子集 x[j] 这样一来， t[j] < x[j] < t[j+k+1] ，用于 j=0, 1,...,n-k-2 。

此例程对系数数组进行补零 c 具有与节点数组相同的长度 t (拖尾 k + 1 系数被评估例程忽略， splev 和 BSpline 。)这与 splprep ，这不会将系数补零。

参考文献

基于中描述的算法 [1], [2], [3], 和 [4]:

1

P.Dierckx，“一种使用样条函数对实验数据进行平滑、微分和积分的算法”，应用数学学报1(1975)165-184。

2

P.Dierckx，“使用样条函数在矩形网格上平滑数据的快速算法”，SIAM J.Numer.Anal。19(1982)1286-1304。

3

P.Dierckx，“一种改进的样条函数曲线拟合算法”，报告TW54。计算机科学，鲁汶大学出版社，1981。

4

P.Dierckx，“用样条拟合曲线和曲面”，“数值分析专著”，牛津大学出版社，1993。

示例

可以使用B样条曲线对一维点进行插值。有关更多示例，请参阅 in the tutorial 。

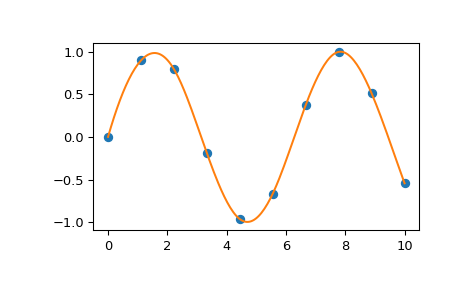
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import splev, splrep
>>> x = np.linspace(0, 10, 10)
>>> y = np.sin(x)
>>> spl = splrep(x, y)
>>> x2 = np.linspace(0, 10, 200)
>>> y2 = splev(x2, spl)
>>> plt.plot(x, y, 'o', x2, y2)
>>> plt.show()

上一页

scipy.interpolate.make_lsq_spline

下一页

scipy.interpolate.splprep