scipy.interpolate.BSpline¶

class scipy.interpolate.BSpline(t, c, k, extrapolate=True, axis=0)[源代码]¶

B样条基中的一元样条。

\[s(X)=\sum_{j=0}^{n-1}c_j B_{j，k；t}(X)\]

哪里 $B_{{j, k; t}}$ 是三次B样条基函数吗 k 和结 t 。

参数

tndarray，形状(n+k+1，): 打结
cndarray，形状(>=n，.): 样条系数
k集成: B样条次数
extrapolate布尔值或‘周期性’，可选: 是否在基准间隔之外进行外推， t[k] .. t[n] ，或退还NANS。如果为True，则外推在基本间隔上活动的第一个和最后一个多项式b样条函数。如果为‘PERIONAL’，则使用周期性外推。默认值为True。
axis整型，可选: 插值轴。默认值为零。

注意事项

B样条基元通过以下方式定义

\[ \begin{align}\begin{aligned}b_{i，0}(X)=1，\texm{if$t_i\le x<t_{i+1}$，否则$0$，}\\B_{i，k}(X)=\frac{x-t_i}{t_{i+k}-t_i}B_{i，k-1}(X) +\frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}B_{i+1，k-1}(X)\end{aligned}\end{align} \]

实施详情

至少 k+1 对于三次样条来说，系数是必需的。 k ，以便 n >= k+1 。附加系数， c[j] 使用 j > n ，则被忽略。
B样条三次基元 k 在上面形成一个统一的隔断 基本间隔 ， t[k] <= x <= t[n] 。

参考文献

1: 汤姆·利奇和克努特·莫肯，样条方法，http://www.uio.no/studier/emner/matnat/ifi/INF-MAT5340/v05/undervisningsmateriale/
2: 卡尔·德布尔：“样条实用指南”，斯普林格，2001年。

示例

将B样条的递归定义转换为Python代码，我们有：

>>> def B(x, k, i, t):
...    if k == 0:
...       return 1.0 if t[i] <= x < t[i+1] else 0.0
...    if t[i+k] == t[i]:
...       c1 = 0.0
...    else:
...       c1 = (x - t[i])/(t[i+k] - t[i]) * B(x, k-1, i, t)
...    if t[i+k+1] == t[i+1]:
...       c2 = 0.0
...    else:
...       c2 = (t[i+k+1] - x)/(t[i+k+1] - t[i+1]) * B(x, k-1, i+1, t)
...    return c1 + c2

>>> def bspline(x, t, c, k):
...    n = len(t) - k - 1
...    assert (n >= k+1) and (len(c) >= n)
...    return sum(c[i] * B(x, k, i, t) for i in range(n))

请注意，这是一种低效(如果简单的话)计算B样条的方法-这个样条类的计算方式与之相当，但效率要高得多。

在这里，我们构造了一个基区间上的二次样条函数 2 <= x <= 4 并与计算样条线的天真方式进行比较：

>>> from scipy.interpolate import BSpline
>>> k = 2
>>> t = [0, 1, 2, 3, 4, 5, 6]
>>> c = [-1, 2, 0, -1]
>>> spl = BSpline(t, c, k)
>>> spl(2.5)
array(1.375)
>>> bspline(2.5, t, c, k)
1.375

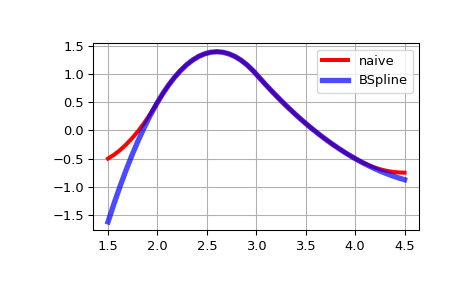
请注意，在基本间隔之外，结果会有所不同。这是因为 BSpline 外推在基本间隔上活动的B样条函数的第一个和最后一个多项式片段。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> xx = np.linspace(1.5, 4.5, 50)
>>> ax.plot(xx, [bspline(x, t, c ,k) for x in xx], 'r-', lw=3, label='naive')
>>> ax.plot(xx, spl(xx), 'b-', lw=4, alpha=0.7, label='BSpline')
>>> ax.grid(True)
>>> ax.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-BSpline-1.png

属性

tndarray: 结向量
cndarray: 样条系数
k集成: 样条次数
extrapolate布尔尔: 如果为True，则外推在基本间隔上活动的第一个和最后一个多项式b样条函数。
axis集成: 插值轴。
tck元组: 相当于 (self.t, self.c, self.k) (只读)。

方法：

`__call__` \(X[, nu, extrapolate] )	计算样条函数。
`basis_element` \(t[, extrapolate] )	返回B样条基元素 `B(x \| t[0], ..., t[k+1])` 。
`derivative` \([nu] )	返回表示导数的B样条。
`antiderivative` \([nu] )	返回表示反导数的B样条。
`integrate` \(a，b[, extrapolate] )	计算样条的定积分。
`construct_fast` \(t，c，k[, extrapolate, axis] )	在不进行检查的情况下构建样条曲线。
`design_matrix` \(X，t，k)	返回CSR格式的设计矩阵。
`from_power_basis` \(PP[, bc_type] )	由幂基中的分段多项式构造B样条基中的多项式。

scipy.interpolate.NdPPoly.construct_fast

scipy.interpolate.BSpline.__call__