椭圆的理论公式及推导过程

理论公式

简介

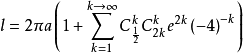
a为椭圆长半轴，e 为椭圆的离心率

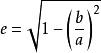
椭圆周长理论公式是存在的不过它不能用初等函数表示，它是一个与离心率有关的无穷收敛级数，本公式已经把正圆周长纳入其中，在某种意义上讲正圆是特殊的椭圆，也就是说正圆是长短轴相等的椭
公式推导是要利用到曲线长度积分，同时关键的一步是，要把椭圆积分利用牛顿二项式定理展开为以sinθ 为变量的级数再通过积分求解。如图。
推导过程
先建立椭圆参数方程：
x=a SINθ
Y=bcosθ
根据曲线长度积分方程：
u=y′

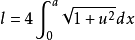
将椭圆方程代入上式得：

（1） L=4a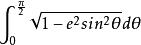
而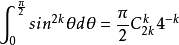
得出将（1）式用牛顿二项式定理展开再逐项积分得：

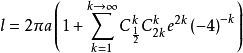
求解完毕（这个公式把a=b带进去以后为圆周长公式，e=1时,L=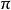a)