摘要: 椭圆定义 椭圆是圆锥曲线的一种，即圆锥与平面的截线。椭圆在开普勒行星运行三定律中扮演了重要角色，即恒星是椭圆两焦点中的一个，是数学科重点研究的一个项目。 第一定义 平面内与两定点F1、F2的距离的和等于常数2a（2a>|F1F2|）的的动点P的轨迹叫做椭圆。...
椭圆定义
椭圆是圆锥曲线的一种，即圆锥与平面的截线。椭圆在开普勒行星运行三定律中扮演了重要角色，即恒星是椭圆两焦点中的一个，是数学科重点研究的一个项目。
第一定义
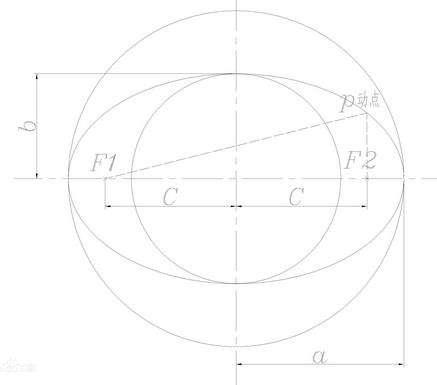
平面内与两定点F1、F2的距离的和等于常数2a（2a>|F1F2|）的的动点P的轨迹叫做椭圆。
即：|PF1|+|PF2|=2a
其中两定点F1、F2叫做椭圆的焦点，两焦点的距离|F1F2|=2c<2a 叫做椭圆的焦距。P为椭圆的动点。
椭圆截与两焦点连线重合的直线所得的弦为长轴，长为2a
椭圆截垂直平分两焦点连线的直线所得弦为短轴，长为2b
\(c^2=a^2-b^2\)可变为\(c=√[a^2-b^2]\)
第二定义
\(X= \frac {a^2}{c} \)平面内到定点F(c,0)的距离和定直线l：\(X= \frac {a^2}{c} \)（F不在l上）的距离之比为常数\( \frac {c}{a} \)（即离心率，0<e<1）的点的轨迹是椭圆。（即准线）
其中定点F为椭圆的焦点，定直线l称为椭圆的准线（该定直线的方程是\(x=± \frac {a^2}{c} \)（焦点在x轴上），或\(y=± \frac {a^2}{c} \)（焦点在y轴上））。
其他定义
根据椭圆的一条重要性质：椭圆上的点与椭圆长轴两端点连线的斜率之积是定值，定值为\(e^2-1\)，可以得出：
在坐标轴内，动点（x,y）到两定点（a,0）（-a,0）的斜率乘积等于常数m（-1<m<0）
注意：考虑到斜率为零时不满足乘积为常数，所以 无法取到，即该定义仅为去掉两个点的椭圆。
椭圆也可看做圆按一定方向作压缩或拉伸一定比例所得图形。
椭圆的标准方程
椭圆的标准方程公分两种情况：
当焦点在x轴时，椭圆的标准方程是：\(x^2/a^2+y^2/b^2=1\)，(a>b>0)；
当焦点在y轴时，椭圆的标准方程是：\(y^2/a^2+x^2/b^2=1\)，(a>b>0)；
